Как меняется энергия фотона при его комптоновском рассеянии

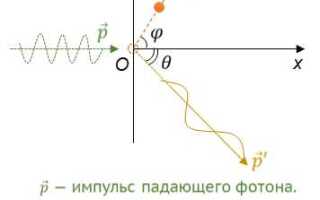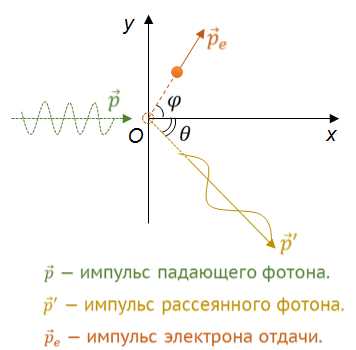
Комптоновское рассеяние – это неупругое взаимодействие фотона с электроном, при котором происходит перераспределение энергии и импульса между частицами. В результате фотон теряет часть своей энергии, которая передаётся электрону, а его длина волны увеличивается. Эффект наиболее выражен при рассеянии на свободных электронах, что делает его ключевым в рентгеновской и гамма-спектроскопии.

Количественно изменение энергии фотона описывается уравнением Комптона: λ’ — λ = (h / m_ec)(1 — cosθ), где λ – начальная длина волны фотона, λ’ – длина волны после рассеяния, h – постоянная Планка, m_e – масса электрона, c – скорость света, θ – угол рассеяния. Из этого уравнения следует, что максимальное изменение длины волны достигается при θ = 180°, когда фотон отражается в обратном направлении.

Энергия фотона после рассеяния определяется выражением: E’ = E / [1 + (E / m_ec²)(1 — cosθ)], где E – начальная энергия фотона. При высоких энергиях (например, выше 100 кэВ) потери энергии становятся существенными, и учет комптоновского эффекта необходим в расчётах доз облучения и при моделировании детекторов ионизирующего излучения.

Для минимизации потерь энергии в системах визуализации и регистрации фотонов применяются материалы с высокой плотностью и атомным номером, поскольку они способствуют уменьшению угла рассеяния и, следовательно, ограничивают энергетическое снижение фотона. В практических задачах важно также учитывать комптоновское уширение спектральных линий при регистрации излучения в детекторах, особенно в диапазоне 50–500 кэВ.

Как зависит энергия рассеянного фотона от угла отклонения

Энергия фотона после комптоновского рассеяния уменьшается и прямо зависит от угла отклонения. Чем больше угол рассеяния, тем меньше энергия рассеянного фотона. Это явление объясняется уравнением Комптона:

E’ = E / [1 + (E / (m_ec²)) · (1 — cosθ)],

где E – начальная энергия фотона, E’ – энергия после рассеяния, m_e – масса электрона, c – скорость света, θ – угол рассеяния.

При θ = 0°, фотон сохраняет свою энергию: E’ = E. При θ = 90°, энергия снижается ощутимо. При θ = 180° (обратное рассеяние), наблюдается максимальное снижение энергии. Например, при E = 511 кэВ (энергия, сравнимая с массой покоя электрона), обратное рассеяние уменьшает энергию почти вдвое.

Для расчётов в практических задачах удобно использовать формулу изменения длины волны: Δλ = (h / m_ec) · (1 — cosθ), где h – постоянная Планка. Эта формула показывает, что при увеличении θ от 0° до 180° изменение длины волны растёт, а энергия E’ обратно пропорциональна длине волны: E’ = hc / λ’.

При моделировании взаимодействия фотонов с веществом необходимо учитывать, что максимальные потери энергии происходят при больших углах отклонения. Это критично в дозиметрии, гамма-спектроскопии и медицинской визуализации, где точный учёт углов комптоновского рассеяния влияет на интерпретацию данных и точность измерений.

Почему фотон теряет энергию при столкновении с электроном

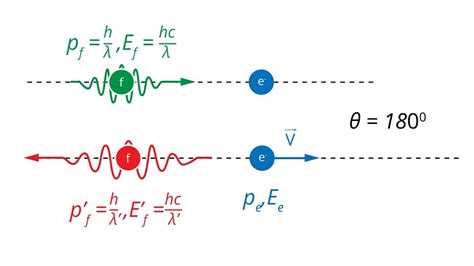
При комптоновском рассеянии фотон сталкивается с электроном, находящимся в покое или обладающим незначительной энергией по сравнению с энергией фотона. В результате взаимодействия происходит передача части энергии фотона электрону, что обусловлено законами сохранения энергии и импульса.

Энергия рассеянного фотона E’ определяется формулой:

E’ = E / (1 + (E / (m_ec²))(1 — cos θ))

где E – начальная энергия фотона, m_e – масса электрона, c – скорость света, θ – угол рассеяния фотона. Чем больше угол θ, тем больше энергия, переданная электрону, и тем сильнее уменьшается энергия фотона.

Снижение энергии связано не с потерями на тепло или сопротивление, а с перераспределением энергии между частицами. Электрон приобретает кинетическую энергию, а фотон продолжает движение с меньшей энергией, что соответствует увеличению его длины волны – явлению, известному как комптоновское смещение:

Δλ = (h / (m_ec)) (1 — cos θ)

где h – постоянная Планка. Эта формула показывает, что изменение длины волны зависит только от угла рассеяния и фундаментальных констант, а не от свойств вещества.

Максимальная потеря энергии фотоном происходит при угле рассеяния 180°, когда электрон получает наибольший импульс. При θ = 0° рассеяние отсутствует, и энергия фотона не изменяется.

Для диагностики комптоновского эффекта в экспериментах используют высокоэнергетические γ-фотоны, поскольку эффект становится значительным только при энергиях, сопоставимых с энергией покоя электрона (511 кэВ).

Как вычислить изменение длины волны при комптоновском эффекте

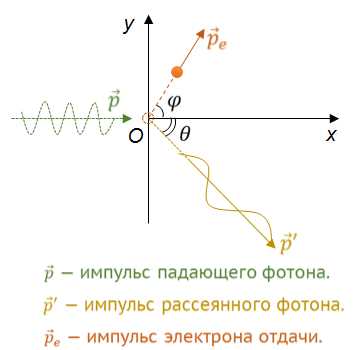
Изменение длины волны фотона при комптоновском рассеянии определяется уравнением:

Δλ = λ’ − λ = (h / (m_ec)) · (1 − cos θ)

Здесь:

• Δλ – изменение длины волны фотона
• λ – исходная длина волны фотона
• λ’ – длина волны рассеянного фотона
• h – постоянная Планка (6.626 × 10⁻³⁴ Дж·с)
• m_e – масса электрона покоя (9.109 × 10⁻³¹ кг)
• c – скорость света в вакууме (3.00 × 10⁸ м/с)
• θ – угол рассеяния фотона относительно начального направления

Постоянная h / (m_ec) имеет значение 2.426 × 10⁻¹² м и называется комптоновской длиной волны электрона.

Для расчёта подставьте значение угла рассеяния в радианах или градусах, преобразовав его через косинус. Например, при θ = 90°, cos θ = 0, и Δλ = 2.426 × 10⁻¹² м.

Если известна энергия исходного фотона, можно вычислить его длину волны по формуле:

λ = hc / E, где E – энергия фотона в джоулях.

Для фотонов с энергией, выраженной в кэВ, используйте λ[нм] = 1.24 / E[кэВ]. Полученное значение можно подставить в уравнение комптоновского сдвига для вычисления новой длины волны после рассеяния.

Влияние начальной энергии фотона на величину потери энергии

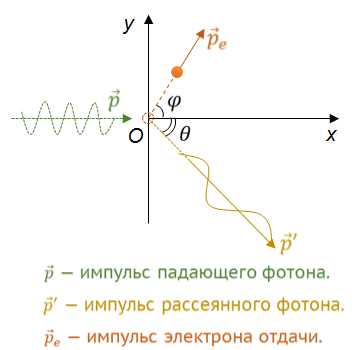
При комптоновском рассеянии изменение энергии фотона определяется углом рассеяния и его начальной энергией. Чем выше энергия исходного фотона, тем меньше относительная потеря энергии при рассеянии на фиксированный угол.

• Для фотонов с энергией до 100 кэВ характерна значительная потеря энергии даже при малых углах рассеяния. Например, при угле 90° фотон с энергией 50 кэВ теряет около 30% своей энергии.
• В диапазоне 500 кэВ – 1 МэВ доля потери энергии снижается. При рассеянии на 90° фотон с энергией 1 МэВ теряет только около 20% энергии.
• Для энергий выше 5 МэВ рассеяние становится все более направленным (вперед), и потеря энергии на единицу угла становится пренебрежимо малой. Например, при 10 МэВ и угле 30° изменение энергии составляет менее 2%.

Зависимость описывается формулой Комптона:

Δλ = (h / (mec)) · (1 - cosθ)

где прирост длины волны обратно пропорционален энергии фотона. При высокой энергии изменение длины волны мало, следовательно, и потеря энергии незначительна.

1. Для получения максимального энерговыбора используют фотоны с энергией до 200 кэВ.
2. При анализе высокоэнергетических спектров (γ-излучение) необходимо учитывать, что даже при рассеянии на большие углы фотон сохраняет значительную часть начальной энергии.
3. Для калибровки спектрометров предпочтительны источники с энергией 100–300 кэВ, где потеря энергии чувствительно зависит от угла рассеяния.

Таким образом, эффективность комптоновского рассеяния как механизма передачи энергии существенно зависит от начальной энергии фотона. Максимальная потеря наблюдается при энергиях до 300 кэВ и углах близких к 180°.

Применение формулы Комптона для расчёта энергии фотона после рассеяния

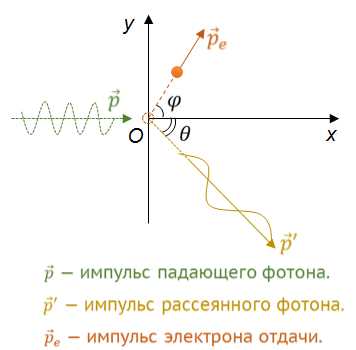
Для определения энергии фотона после комптоновского рассеяния используют выражение, полученное из закона сохранения энергии и импульса:

E’ = E / [1 + (E / (m_ec²)) (1 — cos θ)],

где E – начальная энергия фотона, E’ – энергия после рассеяния, m_e – масса покоя электрона (511 кэВ/с²), c – скорость света, θ – угол рассеяния в радианах.

При увеличении угла рассеяния от 0 до π энергия рассеянного фотона E’ уменьшается. Максимальное снижение энергии наблюдается при θ = 180°, когда рассеяние происходит назад. В этом случае формула принимает вид:

E’ = E / [1 + (2E / (m_ec²))].

Если, например, фотон с энергией 662 кэВ (гамма-квант ¹³⁷Cs) рассеивается на угол 90°, то подставляя значения:

E’ = 662 / [1 + (662 / 511)(1 — cos 90°)] = 662 / [1 + 662 / 511] ≈ 288 кэВ.

Для практических расчётов удобно использовать постоянное значение m_ec² = 511 кэВ, что упрощает численную подстановку. При известных E и θ можно определить не только E’, но и кинетическую энергию электрона: K_e = E — E’.

Формула эффективна при высоких энергиях фотонов (>100 кэВ). При меньших энергиях влияние рассеяния становится незначительным.

Где на практике важно учитывать изменение энергии фотона при рассеянии

Изменение энергии фотона при комптоновском рассеянии критично в ряде точных научных и технических приложений, где фиксируются и анализируются рентгеновские и гамма-лучи.

В медицинской диагностике, особенно в компьютерной томографии с использованием рентгеновского излучения, учет сдвига энергии фотонов позволяет улучшить качество изображений и повысить точность дозиметрии. Игнорирование эффекта приводит к ошибкам в калибровке детекторов и снижению контрастности снимков при высоких энергиях (выше 50 кэВ).

В астрофизике изменение энергии фотонов при рассеянии в космических лучах влияет на анализ спектров рентгеновского излучения звездных и галактических источников. Моделирование комптоновских эффектов помогает корректно определять температуры и плотности межзвездного газа, что существенно для понимания процессов звездообразования и аккреции на черные дыры.

В ядерной физике и дозиметрии гамма-излучения при контроле радиационных фонов учитывают комптоновский эффект для точного определения энергии и интенсивности излучения. Это важно для мониторинга ядерных объектов и безопасности на промышленных предприятиях, где энергия фотонов влияет на выбор защитных материалов и толщину экранов.

В технологиях обратного рассеяния рентгеновских лучей для неразрушающего контроля качества материалов и безопасности (например, при инспекции багажа в аэропортах) сдвиг энергии фотона корректируется для повышения разрешающей способности и надежности выявления скрытых объектов.

В экспериментальных установках на ускорителях частиц и рентгеновских лазерах точное измерение комптоновского эффекта необходимо для калибровки детекторов и интерпретации спектров излучения, что напрямую влияет на результаты исследований фундаментальных взаимодействий и разработку новых методов диагностики материалов.

Вопрос-ответ:

Почему при комптоновском рассеянии энергия фотона изменяется?

Энергия фотона меняется из-за взаимодействия с электроном. В процессе столкновения фотон передаёт часть своей энергии электрону, который получает импульс и начинает двигаться. В результате фотон теряет часть энергии, и его длина волны увеличивается.

Как связаны длина волны фотона и его энергия после рассеяния?

Длина волны фотона обратно пропорциональна его энергии: чем больше длина волны, тем меньше энергия. При комптоновском рассеянии длина волны фотона увеличивается, поэтому его энергия уменьшается. Изменение длины волны зависит от угла рассеяния и определяется формулой, введённой Комптоном.

Можно ли использовать эффект Комптона для измерения энергии электронов?

Да, этот эффект позволяет оценивать энергию электронов, поскольку при рассеянии фотон теряет определённое количество энергии, которое идёт на увеличение кинетической энергии электрона. Измеряя изменение длины волны и угол рассеяния, можно вычислить энергию движущихся электронов.

Какие параметры влияют на величину изменения энергии фотона в комптоновском рассеянии?

Основными факторами являются угол рассеяния фотона и масса электрона. Чем больше угол рассеяния, тем сильнее уменьшается энергия фотона. Масса электрона определяет, сколько энергии может быть передано. Кроме того, исходная энергия фотона задаёт начальные условия процесса.

Почему комптоновское рассеяние важно для понимания природы света и материи?

Этот процесс демонстрирует корпускулярные свойства света, показывая, что фотон ведёт себя как частица с определённой энергией и импульсом. Одновременно взаимодействие с электронами показывает квантовую природу материи. Это явление стало ключевым доказательством фотонной теории света и помогло развить квантовую механику.