Дельта u (или изменение напряжения) в электрических цепях является важным параметром для анализа работы как линейных, так и нелинейных систем. Рассчитав этот параметр, можно точно оценить, как изменяется напряжение на элементах цепи в ответ на изменения других характеристик, таких как ток или сопротивление. Это знание позволяет предсказать поведение цепи и корректно выбрать компоненты для ее сборки или оптимизации.
Для расчета дельта u в типичных электрических цепях используется закон Ома. В простейшем случае, изменение напряжения на сопротивлении можно выразить через изменение тока. Формула имеет вид: ΔU = R * ΔI, где ΔU – изменение напряжения, R – сопротивление элемента цепи, а ΔI – изменение тока. В более сложных схемах, где имеются активные и пассивные компоненты, следует учитывать их взаимное влияние через эквивалентные схемы.
Когда в цепи присутствуют индуктивные и емкостные элементы, расчет становится более сложным и требует учета фазовых сдвигов. В таких случаях для получения точного значения дельта u применяется комплексное представление напряжения и тока. Важно помнить, что изменение напряжения в индуктивных и емкостных цепях также зависит от частоты тока, и это необходимо учитывать при расчетах для переменного тока.
Определение дельта u: что это и зачем нужно
Применение дельта u важно для точного расчёта напряжения в различных участках цепи. Например, при расчёте падения напряжения на резисторах или других элементах, ΔU используется для получения точных значений, что критично для корректной работы устройства. Неопределённость в значении ΔU может привести к неточности в проектировании и эксплуатации электрических систем.
Для вычисления дельта u необходимо учесть сопротивление элементов цепи и величину тока, протекающего через них. Формула для расчёта будет зависеть от конкретной ситуации: для простого резистора – это закон Ома, для более сложных цепей – методы, такие как анализ с использованием законов Кирхгофа.
Важность правильного определения ΔU заключается также в том, что оно влияет на безопасность эксплуатации цепей. Перегрузка по напряжению может вызвать повреждение компонентов, короткие замыкания или даже возгорания. Поэтому точные расчёты необходимы для предотвращения таких рисков.
Таким образом, понимание и правильное использование дельта u позволяет инженерам и специалистам по электротехнике обеспечивать стабильность и безопасность работы электрических систем, а также оптимизировать их эффективность.
Как вычислить разницу потенциалов для резистивных цепей
Для вычисления разницы потенциалов (дельта U) в резистивной цепи необходимо учитывать закон Ома и распределение напряжения по элементам цепи. Разница потенциалов между двумя точками в цепи пропорциональна току и сопротивлению между ними. Рассмотрим основные шаги для вычисления напряжения в различных схемах.
1. В простейшей последовательной цепи разница потенциалов на каждом резисторе определяется по формуле: U = I * R, где I – ток в цепи, R – сопротивление резистора. Поскольку ток одинаков во всей цепи, достаточно умножить его на сопротивление каждого элемента для нахождения напряжения на нём.
2. В параллельной цепи напряжение на каждом резисторе одинаково и равно общему напряжению источника. Таким образом, разницу потенциалов можно вычислить напрямую по формуле: U = U_источник, где U_источник – напряжение источника питания.
3. Для сложных цепей, включающих как последовательное, так и параллельное соединение резисторов, нужно сначала найти эквивалентное сопротивление цепи. Для последовательного соединения: R_экв = R_1 + R_2 + … + R_n, для параллельного: 1/R_экв = 1/R_1 + 1/R_2 + … + 1/R_n. После нахождения эквивалентного сопротивления вычисляем ток по закону Ома, а затем – разницу потенциалов на каждом элементе цепи.
4. В цепях с несколькими источниками напряжения разницу потенциалов можно вычислить методом суперпозиции, поочередно учитывая каждый источник напряжения при нулевом значении остальных. После этого результат комбинируется для получения общей разницы потенциалов.
Рассчитывая напряжение в резистивных цепях, всегда важно учитывать полное сопротивление и ток, протекающий через элементы. Это позволит точно определить разницу потенциалов в различных точках цепи.
Применение закона Ома для расчета дельта u в цепях с постоянным током
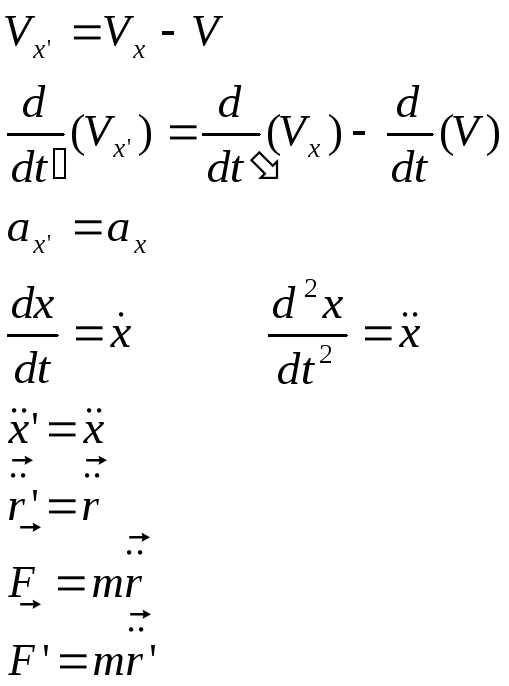
U = I × R
Здесь U – это напряжение (дельта u), I – ток, а R – сопротивление элемента цепи. Рассмотрим, как можно применить этот закон для расчета изменения напряжения (дельта u) на конкретных участках цепи.
- Расчет дельта u через сопротивление: Если известно значение тока и сопротивления, дельта u можно вычислить напрямую. Например, если сопротивление составляет 10 Ом, а ток – 2 А, то дельта u = 2 А × 10 Ом = 20 В.
- Учет изменений тока: Если в цепи происходит изменение тока, то напряжение на элементе также изменяется пропорционально. Это важно для цепей с переменными токами, но в случае постоянного тока расчет остается стабильным и можно использовать средние значения тока для упрощения вычислений.
- Влияние параллельных и последовательных соединений: Для цепей, состоящих из нескольких компонентов, важно учитывать тип соединения. В последовательных цепях ток одинаков на всех элементах, а напряжение пропорционально сопротивлению. В параллельных – напряжение одинаково на всех элементах, а ток пропорционален их проводимости.
Для точных расчетов важно использовать точные значения сопротивлений элементов цепи, а также учитывать возможные изменения температуры, так как сопротивление проводников может изменяться в зависимости от температурных колебаний.
Таким образом, расчет дельта u в цепях с постоянным током сводится к точному применению закона Ома, что позволяет эффективно и быстро определить напряжение на различных участках электрической цепи.
Как рассчитать дельта u в цепях с переменным током
Для расчета разности потенциалов (дельта u) в цепях с переменным током важно учитывать параметры, такие как амплитуда напряжения, сопротивление, индуктивность и емкость элементов цепи. Применение закона Ома для переменного тока потребует учета комплексных сопротивлений.
Если цепь состоит только из резистора, то разница потенциалов между двумя точками можно вычислить как произведение тока на сопротивление:
U = I × R
Для более сложных цепей, содержащих индуктивные и ёмкостные элементы, следует использовать комплексные импедансы (Z). В этом случае напряжение на каждом элементе цепи рассчитывается по формуле:
U = I × Z
где Z – это комплексное сопротивление, которое зависит от частоты тока и параметров индуктивности или ёмкости. Для индуктивности Z = jωL, для ёмкости Z = 1 / jωC, где j – мнимая единица, ω – угловая частота (ω = 2πf), L – индуктивность, C – ёмкость, а f – частота сигнала.
Если цепь состоит из нескольких элементов, напряжение можно рассчитать через сложение комплексных напряжений на каждом из элементов. Для цепей с параллельными и последовательными соединениями сопротивления суммируются по определённым правилам для комплексных чисел.
В случае синусоидального сигнала напряжения и тока, разность потенциалов может быть выражена как амплитуда напряжения, умноженная на фазовый угол между током и напряжением:
U = U₀ × cos(φ)
где U₀ – амплитуда напряжения, φ – фазовый угол между током и напряжением. Для расчёта точной разности потенциалов в цепи с переменным током важно учитывать фазовые сдвиги, так как они могут существенно влиять на конечный результат.
Для практического применения следует помнить, что в цепях с переменным током существуют резонансные частоты, при которых реактивные сопротивления (индуктивные и ёмкостные) компенсируют друг друга, что приводит к минимизации общего сопротивления и максимальному току в цепи. Это явление также важно учитывать при расчёте разности потенциалов.
Как учесть индуктивность и ёмкость при расчете разницы потенциалов

При расчете разницы потенциалов в электрических цепях, включающих индуктивные и ёмкостные элементы, важно учитывать их влияние на фазовые сдвиги и амплитуды напряжений. Индуктивность и ёмкость влияют на реактивное сопротивление цепи, что приводит к изменению напряжений в зависимости от частоты сигнала.
Индуктивность (L) вызывает фазовый сдвиг между током и напряжением, при этом ток отстает от напряжения на 90 градусов при синусоидальном сигнале. Для учета индуктивности необходимо учитывать её реактивное сопротивление, которое выражается через формулу:
Z_L = jωL,
где j – мнимая единица, ω – угловая частота сигнала, L – индуктивность элемента. Это сопротивление изменяет фазовый угол и амплитуду напряжения на катушке индуктивности в цепи.
Ёмкость (C) имеет противоположное воздействие: ток опережает напряжение на 90 градусов. Реактивное сопротивление ёмкости рассчитывается по формуле:
Z_C = 1 / jωC,
где C – ёмкость элемента. С увеличением частоты сопротивление ёмкости уменьшается, что также влияет на распределение напряжений в цепи.
При расчете разницы потенциалов важно учитывать взаимодействие этих двух элементов. В цепи, содержащей как индуктивность, так и ёмкость, суммарное реактивное сопротивление будет определяться комплексным сочетанием их эффектов. Для полной оценки напряжения на каждом элементе цепи нужно учитывать как активные, так и реактивные сопротивления, что обычно делает расчёт более сложным, требующим применения комплексных чисел и фазовых диаграмм.
Чтобы правильно учесть индуктивность и ёмкость, можно использовать метод комплексных импедансов. Он позволяет учитывать не только величину, но и фазовый сдвиг каждого элемента цепи, что важно для точного расчета разницы потенциалов в динамических условиях.
Практические ошибки при расчете дельта u и как их избежать
При расчете разности потенциалов (дельта u) в электрических цепях можно столкнуться с несколькими распространенными ошибками, которые существенно искажают результаты. Эти ошибки часто связаны с неправильной интерпретацией закона Ома и неграмотным применением теоремы Кирхгофа.
1. Неверное определение точек отсчета для измерения напряжения
Часто начинающие инженеры неправильно выбирают точки для измерения напряжения, что приводит к неверному определению разности потенциалов. Напряжение между двумя точками цепи рассчитывается как разность потенциалов между ними, но важно учитывать, что потенциал всегда измеряется относительно некоторой опорной точки. Ошибка может возникнуть, если эта опорная точка не является общим или нейтральным проводом, или если точки измерения выбраны неправильно в контексте схемы.
2. Игнорирование сопротивлений проводников
В реальных цепях сопротивление проводников не является нулевым, что иногда приводит к недооценке падений напряжения. В цепях с длинными проводниками или с малыми токами это может оказать значительное влияние на точность расчета дельта u. Нужно всегда учитывать сопротивление проводников, особенно в сложных схемах.
3. Недооценка влияния параллельных и последовательных элементов
При расчете разности потенциалов важно правильно учитывать распределение напряжений по элементам цепи. Например, в случае параллельных резисторов напряжение на каждом из них одно и то же, а в последовательных – разность потенциалов распределяется пропорционально сопротивлениям. Часто ошибка возникает из-за неверного применения законов Ома и Кирхгофа, что приводит к неправильному распределению напряжений по цепи.
4. Неправильный выбор метода расчета
Для простых цепей достаточно использования закона Ома, но в сложных схемах необходимо применять методы теоремы суперпозиции или метод узловых потенциалов. Ошибки часто возникают, если пытаются использовать один и тот же подход для всех типов схем, что может привести к значительным погрешностям. Важно выбирать метод, который соответствует структуре электрической цепи.
5. Пренебрежение влиянием температурных изменений
Температурные изменения влияют на сопротивление материалов, и это может привести к изменению разности потенциалов. Особенно это важно при расчетах в цепях с компонентами, чувствительными к изменениям температуры. Погрешности могут быть значительными в случае использования цепей с высоким током или в условиях, где температурные колебания велики. Чтобы избежать этой ошибки, следует учитывать температурный коэффициент сопротивления материалов и соответствующим образом корректировать расчеты.
Рекомендации:
Чтобы минимизировать ошибки, рекомендуется:
- Тщательно проверять выбор опорной точки для измерения напряжения.
- Учитывать сопротивление проводников, особенно в длинных цепях.
- Правильно распределять напряжения в цепях с параллельными и последовательными элементами.
- Выбирать правильный метод расчета в зависимости от структуры схемы.
- При необходимости учитывать температурные изменения и их влияние на сопротивление.
Использование мультиметра для измерения дельта u в реальных цепях
Прежде всего, мультиметр должен быть настроен на измерение постоянного или переменного напряжения в зависимости от характеристик цепи. Для большинства мультиметров этот режим выбирается с помощью поворотного переключателя. Важно, чтобы значение измеряемого напряжения не превышало максимально допустимое для устройства, иначе можно повредить мультиметр.
Когда мультиметр настроен на соответствующий режим, следует правильно подключить щупы к цепи. Один щуп должен быть подключен к точке с более высоким потенциалом, а другой – к точке с более низким. Напряжение между этими точками и будет составлять дельта u. Если цепь имеет несколько точек, важно точно выбрать те, которые требуют измерения.
В реальных цепях часто встречаются электромагнитные помехи, которые могут искажать показания. Чтобы минимизировать их влияние, важно размещать щупы как можно ближе друг к другу и избегать лишних длинных проводов. Для точных измерений также следует избегать контакта щупов с другими металлическими частями цепи, чтобы избежать случайных коротких замыканий.
Еще одним важным моментом является проверка состояния мультиметра. Перед использованием стоит проверить его исправность, особенно если прибор долго не использовался. Неисправности, такие как поврежденные щупы или проблемы с батареей, могут привести к неточным измерениям.
Для повышения точности измерений рекомендуется использовать мультиметры с автоопределением диапазона. Такие устройства автоматически выбирают подходящий диапазон измерений в зависимости от величины напряжения, что снижает вероятность ошибок при настройке прибора.
Итак, чтобы точно измерить дельта u в реальной цепи с помощью мультиметра, необходимо соблюдать несколько условий: правильная настройка прибора, минимизация внешних помех, аккуратное подключение щупов и проверка состояния устройства.
Вопрос-ответ:
Что такое дельта u в электрических цепях и как её рассчитать?
Дельта u (или изменение напряжения) в электрических цепях — это разница напряжений между двумя точками в цепи. Для её расчета нужно вычислить напряжение в первой точке и во второй, затем вычесть одно из другого. Формула расчета: ΔU = U1 — U2, где U1 — напряжение в первой точке, U2 — напряжение во второй. Это значение важно для определения потерь энергии и характеристик работы цепи.
Почему важно учитывать дельта u при проектировании электрических цепей?
Учет изменения напряжения в электрических цепях помогает предотвратить перепады напряжения, которые могут привести к повреждению оборудования. Это также влияет на правильную работу компонентов, таких как резисторы, конденсаторы и источники питания. Когда расчет дельта u не проводится, это может повлиять на стабильность работы всей цепи и снизить её эффективность.
Как можно рассчитать дельта u в цепи с несколькими резисторами?
Если в цепи несколько резисторов, то для расчета дельта u нужно учесть их последовательное или параллельное соединение. При последовательном соединении суммарное сопротивление цепи равно сумме сопротивлений всех резисторов, и напряжение будет делиться пропорционально сопротивлениям. Для параллельного соединения общее сопротивление рассчитывается по другой формуле, и напряжение будет одинаковым на всех резисторах. Напряжение на каждом резисторе можно найти, используя закон Ома: U = I * R, где I — ток в цепи, а R — сопротивление.
Какие методы используются для измерения дельта u в реальных электрических цепях?
Для измерения изменения напряжения в электрических цепях обычно используют мультиметры или вольтметры. Мультиметр позволяет измерить напряжение между двумя точками в цепи с высокой точностью. Важно правильно подключить прибор, чтобы не повредить компоненты цепи. Иногда, если цепь сложная, используют осциллографы для наблюдения за динамическими изменениями напряжения во времени.
Как изменение дельта u влияет на работу электрических устройств?
Изменение напряжения (дельта u) может оказывать большое влияние на работу электрических устройств. Если напряжение в цепи становится слишком высоким или низким, это может привести к неправильной работе устройства, перегреву или даже поломке. Например, при недостаточном напряжении устройства не будут работать на полной мощности, а при избытке — могут быть повреждены. Поэтому важно тщательно рассчитывать и контролировать напряжение на различных участках цепи.
Что такое дельта u в электрических цепях и как её рассчитывать?
Дельта u (или разность потенциалов) в электрических цепях — это разница в электрическом потенциале между двумя точками цепи. Чтобы рассчитать её, необходимо измерить напряжение между этими точками. В зависимости от конфигурации цепи и её компонентов (например, резисторов, источников тока или напряжения), можно использовать законы Ома или Кирхгофа для вычислений. Например, в простой цепи с резистором можно найти дельту u, умножив сопротивление на ток, проходящий через цепь.
Как правильно учитывать все параметры при расчёте дельта u в сложных цепях?
При расчёте дельта u в сложных электрических цепях важно учитывать не только сопротивление, но и расположение источников тока или напряжения. В случае последовательного соединения элементов напряжение делится пропорционально сопротивлению, а в случае параллельного — распределяется по закону Кирхгофа. При наличии нескольких источников тока или напряжения нужно использовать принцип суперпозиции, а также учитывать сопротивление всей цепи. Важно правильно учитывать все соединения и токи, чтобы точно рассчитать разность потенциалов.