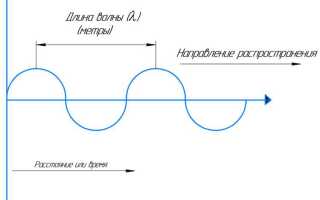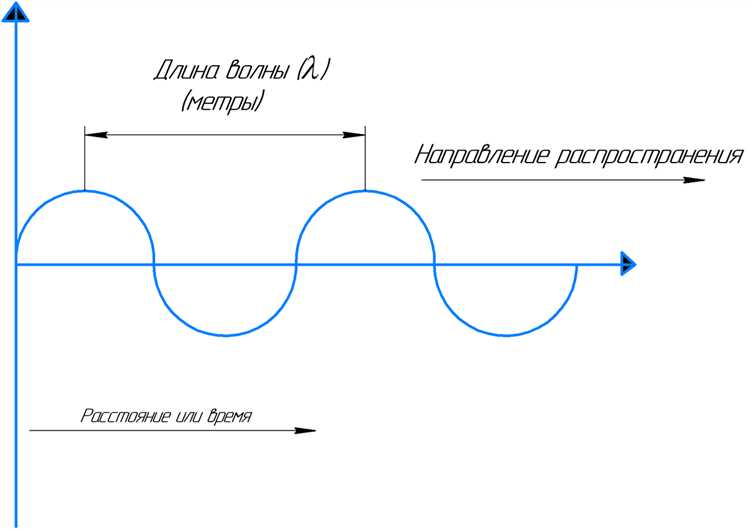
Длина электромагнитной волны напрямую связана с частотой и скоростью распространения волны в данной среде. Основное уравнение для определения длины волны – λ = c / f, где λ – длина волны в метрах, c – скорость света в вакууме, равная приблизительно 299 792 458 м/с, а f – частота волны в герцах.
Для расчёта длины волны в других средах необходимо учитывать показатель преломления n, который снижает скорость распространения: λ = (c / n) / f. Этот показатель определяется материалом и температурными условиями, что критично при точных измерениях и проектировании радиочастотных систем.
При работе с высокими частотами (сотни мегагерц и выше) важно учитывать влияние окружающей среды на скорость волны и соответственно на длину, особенно в волноводах и антеннах. Корректное применение формулы позволяет оптимизировать параметры устройств для достижения максимальной эффективности передачи сигнала.
Как связаны длина волны, частота и скорость света
Частота определяет количество колебаний волны в секунду, измеряется в герцах (Гц). При увеличении частоты длина волны уменьшается пропорционально, поскольку произведение длины волны на частоту всегда равно скорости света.
При расчётах в средах с отличной от вакуума проницаемостью скорость света уменьшается, и формула преобразуется с учётом показателя преломления n: λ = c / (n·ν). Это необходимо учитывать при работе с волнами в оптических материалах и атмосфере.
Для точных вычислений длины волны рекомендуется использовать значение скорости света с точностью не менее 10⁻⁹, особенно в научных и инженерных задачах, связанных с радиочастотами и оптикой.
Метод вычисления длины волны через частоту сигнала
Длина электромагнитной волны λ определяется отношением скорости распространения волны в среде к её частоте f. Для свободного пространства скорость равна скорости света c ≈ 299 792 458 м/с. Формула вычисления длины волны выглядит так:
λ = c / f
где λ – длина волны в метрах, c – скорость света в м/с, f – частота сигнала в герцах (Гц).
Для практических расчетов важно учитывать точное значение частоты. Например, при частоте 1 ГГц (1 × 109 Гц) длина волны составит около 0,2998 м.
Если сигнал распространяется в среде с показателем преломления n, скорость уменьшается до v = c / n, и формула принимает вид:
λ = v / f = (c / n) / f
В таких условиях необходимо знать значение n для корректного вычисления длины волны. При работе с волнами в атмосфере или диэлектрических материалах учитывайте их параметры.
При заданной частоте сигнала длина волны вычисляется напрямую без дополнительных измерений, что ускоряет процесс анализа характеристик сигнала и проектирования антенн.
Для повышения точности рекомендуется использовать частотные генераторы с низким фазовым шумом и точные измерительные приборы, чтобы избежать ошибок в определении частоты.
Использование скорости света в вакууме для расчётов
Скорость света в вакууме строго определена и составляет 299 792 458 м/с. Это фундаментальная константа, используемая для точного вычисления длины электромагнитной волны по формуле λ = c / f, где λ – длина волны, c – скорость света, f – частота волны.
Применение именно скорости света в вакууме исключает погрешности, связанные с прохождением волн через среды с различной оптической плотностью. Для расчётов в условиях других сред необходимо учитывать показатель преломления, но базовый расчет всегда начинается с величины c.
Для повышения точности измерений частоту следует задавать с использованием эталонных генераторов, работающих в стабильном диапазоне. При этом точность длины волны напрямую зависит от корректности значения c, поэтому использование стандартного значения скорости света обязательно для согласованности результатов.
При вычислениях с большими диапазонами частот рекомендуется использовать единицы СИ, чтобы избежать ошибок в масштабах и привести результаты к единому стандарту. Упрощённые значения скорости света (например, 3·10⁸ м/с) допускаются только для предварительных оценок.
Расчёт длины волны в различных средах с учётом показателя преломления
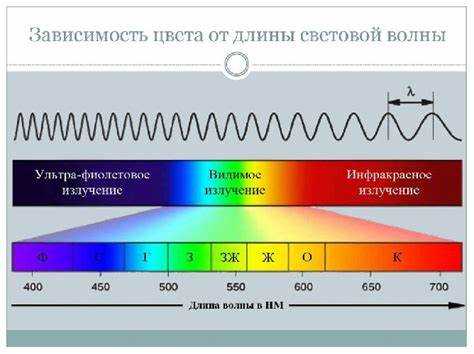
Длина электромагнитной волны в среде определяется формулой λ = λ₀ / n, где λ₀ – длина волны в вакууме, n – показатель преломления среды. Значение n отражает отношение скорости света в вакууме к скорости света в рассматриваемой среде.
Для точных расчётов важно учитывать, что показатель преломления зависит от частоты волны и состава среды. Например, для видимого света в стекле n колеблется от 1,5 до 1,7, что уменьшает длину волны почти в два раза по сравнению с вакуумом. В воде n около 1,33, соответственно длина волны уменьшается примерно на треть.
Если задана частота f и скорость света в вакууме c ≈ 3·10⁸ м/с, длина волны в среде вычисляется через скорость света в среде
Применение формулы длины волны в радиотехнике и связи
- Антенны: Размеры антенн напрямую зависят от длины волны. Для эффективного излучения длина антенны обычно составляет λ/2 или λ/4. Неправильный расчет приводит к снижению КПД и ухудшению направленности сигнала.
- Выбор частотных диапазонов: При планировании частот связи длина волны влияет на проникновение сигнала через препятствия и дальность действия. Короткие волны (несколько метров) подходят для дальних связей через отражения и ионосферу, а длинные (десятки метров и более) – для локальн
Погрешности и ограничения при вычислении длины волны
Длина электромагнитной волны рассчитывается по формуле λ = c / f, где c – скорость света в среде, f – частота сигнала. Основные источники погрешности связаны с точностью определения этих параметров.
Скорость света в вакууме равна примерно 299 792 458 м/с и является константой, однако при прохождении через различные среды (воздух, вода, диэлектрики) скорость уменьшается. Для воздуха поправка составляет порядка 0,03%, что при длинах волн в диапазоне метров приводит к ошибке около нескольких миллиметров. В оптоволокне или других средах с высоким показателем преломления погрешность может достигать 10–20% без учета поправочного коэффициента.
Частота источника измеряется с помощью спектральных анализаторов или частотомеров. В бытовых приборах погрешность может составлять от 0,01% до 0,1%, а в лабораторных условиях – менее 0,001%. При высокочастотных сигналам даже небольшая неточность приводит к заметным отклонениям в длине волны, особенно в диапазоне СВЧ и выше.
Температурные и атмосферные условия влияют на измерение скорости распространения волны, поэтому при точных расчетах рекомендуется использовать данные о температуре, влажности и давлении воздуха для корректировки c. Отсутствие таких данных повышает суммарную ошибку.
Формула λ = c / f предполагает идеальную гармоническую волну. В случае широкой полосы частот или модуляции вычисленная длина будет усреднённой, что снижает точность для конкретных компонентов спектра. В таких случаях рекомендуется использовать спектральный анализ с последующим определением длины волны для каждой частоты отдельно.
При измерениях на практике необходимо учитывать геометрические искажения, влияние отражений и интерференций, которые могут искажать фактическое распространение волны, что не отражается в формуле. Для уменьшения ошибок следует проводить измерения в экранированных камерах или применять методы компенсации многолучевого распространения.
Практические примеры расчёта длины электромагнитной волны

Длина волны (λ) определяется формулой λ = c / f, где c – скорость света в вакууме (примерно 3·10⁸ м/с), а f – частота в герцах.
Пример 1. Радиоволна с частотой 100 МГц. Подставляем: λ = 3·10⁸ / (100·10⁶) = 3 метра. Такая длина характерна для FM-радиостанций.
Пример 2. Микроволновое излучение с частотой 2,4 ГГц (частота Wi-Fi). λ = 3·10⁸ / (2,4·10⁹) ≈ 0,125 метра (12,5 см). Это соответствует размеру волны, который учитывается при проектировании антенн для беспроводных устройств.
Пример 3. Инфракрасное излучение с частотой 4·10¹⁴ Гц. λ = 3·10⁸ / 4·10¹⁴ = 7,5·10⁻⁷ метра (750 нанометров), что соответствует длине волны ближнего инфракрасного диапазона.
Для расчётов в средах с показателем преломления n скорость света корректируют: c’ = c / n. Например, в стекле (n ≈ 1,5) длина волны уменьшается на треть относительно вакуума.
Рекомендуется использовать точные значения частоты и показателя преломления для высокоточных расчётов, особенно в оптических и микроволновых приложениях.
Вопрос-ответ:
Что такое длина электромагнитной волны и как её вычислить?
Длина электромагнитной волны — это расстояние между двумя соседними точками, находящимися в одинаковой фазе колебаний, например, между двумя максимумами. Формула для расчёта длины волны выглядит так: λ = c / f, где λ — длина волны, c — скорость света в вакууме (около 299 792 458 м/с), а f — частота волны. Зная частоту, можно легко определить длину волны.
Почему скорость света используется именно в этой формуле для длины волны?
Скорость света в вакууме — это скорость распространения электромагнитных волн. Она постоянна и универсальна, поэтому в формуле длины волны именно её используют. Для других сред скорость может изменяться, что влияет на длину волны, но в вакууме именно эта величина — базовая характеристика.
Как изменится длина электромагнитной волны, если увеличить её частоту?
Длина волны обратно пропорциональна частоте. Это значит, что при увеличении частоты длина волны становится меньше. Например, если частота удваивается, длина волны уменьшается в два раза. Такая зависимость объясняется формулой λ = c / f.
Можно ли использовать формулу λ = c / f для волн, распространяющихся в средах, отличных от вакуума?
Формула в её классическом виде применима для волн в вакууме, где скорость света постоянна. В других средах скорость электромагнитной волны меньше из-за оптической плотности материала. Тогда вместо c используют скорость распространения в конкретной среде, которая равна c, делённой на показатель преломления среды. Таким образом, длина волны будет меньше, чем в вакууме.
Какую роль играет частота в определении длины электромагнитной волны и её свойствах?
Частота характеризует, сколько колебаний происходит в секунду. Она напрямую влияет на длину волны: чем выше частота, тем короче длина. Частота также связана с энергией волны и её взаимодействием с веществом. Например, радиоволны имеют низкую частоту и длинные волны, а рентгеновские лучи — высокую частоту и короткие волны.
Как связаны скорость света, частота и длина электромагнитной волны в формуле для её вычисления?
Длина волны определяется как отношение скорости распространения волны к её частоте. В случае электромагнитных волн, которые в вакууме распространяются со скоростью света (приблизительно 299 792 458 м/с), длина волны λ вычисляется по формуле: λ = c / f, где c — скорость света, а f — частота волны. Это значит, что при увеличении частоты длина волны уменьшается, и наоборот.
Почему формула для длины электромагнитной волны не меняется в различных средах?
Формула длины волны в виде λ = c / f верна для волн, распространяющихся в вакууме, где скорость равна скорости света c. В средах с отличной от вакуума проницаемостью скорость волны уменьшается, поэтому формула модифицируется: λ = v / f, где v — скорость волны в конкретной среде. Следовательно, в разных материалах длина волны при той же частоте будет отличаться, поскольку скорость распространения меняется, но сам принцип вычисления остаётся прежним.