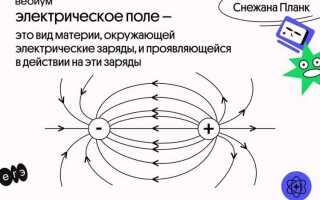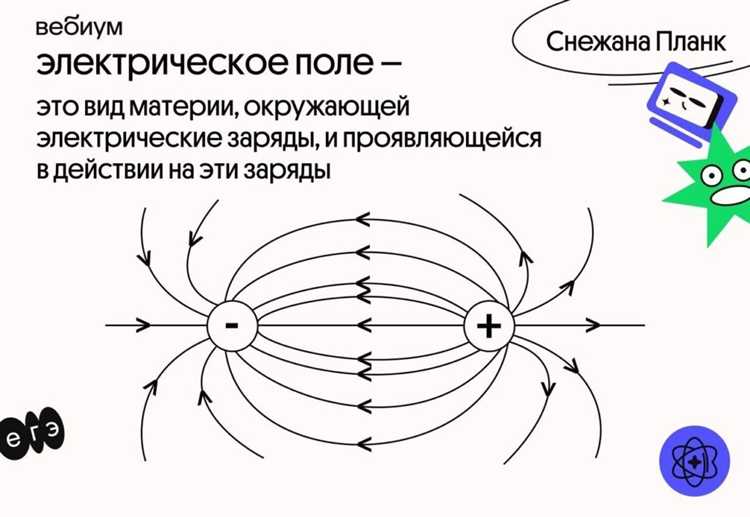
Напряженность электрического поля – это векторная физическая величина, определяющая силу, действующую на единичный положительный заряд, помещённый в данную точку поля. Измеряется в вольтах на метр (В/м) или ньютон на кулон (Н/Кл), и отражает интенсивность взаимодействия между зарядами.
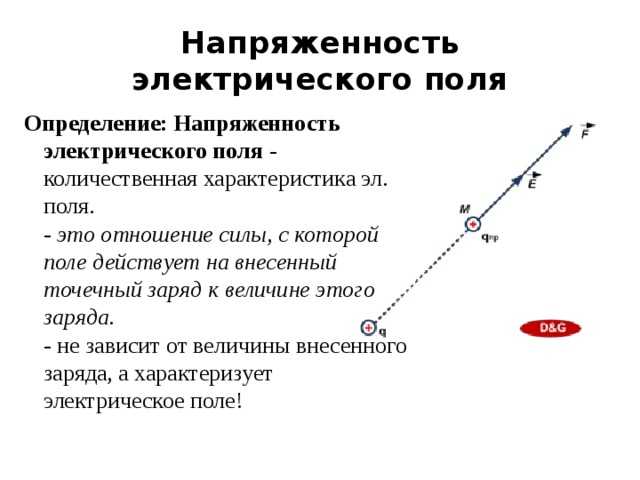
Формально напряженность определяется как отношение силы, действующей на пробный заряд, к величине этого заряда: E = F / q. Это позволяет анализировать распределение электрического поля без учета влияния самого пробного заряда, что критично для точных расчетов в электростатике и электронике.
При практическом использовании важно учитывать, что напряженность напрямую связана с изменением потенциала поля: E = -dV/dl, где dV – изменение электрического потенциала, а dl – расстояние между точками. Это соотношение лежит в основе методов измерения и моделирования электрических полей в различных инженерных задачах, включая проектирование изоляции и анализ пробоя материалов.
Величина, характеризующая напряженность электрического поля
Формула для напряженности электрического поля в точке, расположенной на расстоянии r от точечного заряда Q, имеет вид:
E = k * |Q| / r²
- k – постоянная электрической связи, равная 8.
Как измеряется напряженность электрического поля на практике?

Измерение напряженности электрического поля основано на определении силы, действующей на пробный заряд, или на измерении разности потенциалов между двумя точками. Наиболее распространённый метод – использование электростатического вольтметра или зонда напряженности поля (например, зонда Кельвина).
<
Что влияет на величину напряженности электрического поля в разных материалах?

Напряженность электрического поля (E) в материале определяется не только приложенным напряжением, но и его внутренними свойствами. Важнейший фактор – диэлектрическая проницаемость (ε), которая характеризует способность среды ослаблять электрическое поле за счет поляризации. Чем выше ε, тем ниже напряженность поля при том же внешнем напряжении.
Проводящие материалы почти полностью компенсируют внешнее поле за счет свободных зарядов, поэтому напряженность внутри проводника стремится к нулю. В полупроводниках и диэлектриках с меньшей подвижностью зарядов напряженность зависит от степени легирования и наличия дефектов, которые могут создавать локальные поля, изменяющие распределение напряженности.
Структурные особенности материала, такие как неоднородности и пористость, влияют на локальные значения напряженности поля. В зонах с меньшей диэлектрической проницаемостью напряженность увеличивается, что важно учитывать при проектировании композитных материалов и изоляции.
Температурные изменения влияют на диэлектрическую проницаемость и подвижность зарядов, изменяя напряженность поля. При повышении температуры ε часто снижается, что ведет к увеличению локальной напряженности при постоянном приложенном напряжении.
При работе с разными материалами рекомендуется учитывать конкретные значения ε, контролировать структуру для минимизации неоднородностей и избегать условий, способствующих повышению температуры, чтобы поддерживать стабильную величину напряженности электрического поля.
Как вычислить напряженность электрического поля вокруг точечного заряда?
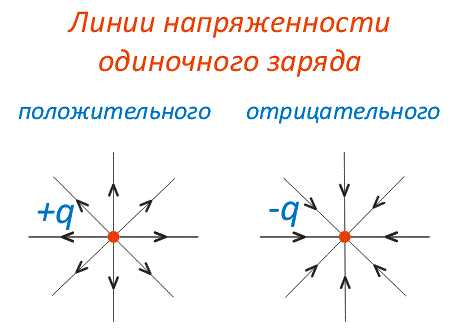
Для вычисления напряженности электрического поля вокруг точечного заряда используется закон Кулона, который определяет силу взаимодействия между двумя точечными зарядами. Напряженность электрического поля \( E \) в точке пространства зависит от величины заряда \( Q \), расстояния \( r \) от заряда до этой точки и константы электрической проницаемости среды.
Основная формула для напряженности электрического поля выглядит следующим образом:
E = \frac{k \cdot Q}{r^2}
- E – напряженность электрического поля, измеряется в вольтах на метр (В/м).
- k – электрическая постоянная (постоянная Кулона), равная \( 8.99 \times 10^9 \ \text{Н} \cdot \text{м}^2 / \text{Кл}^2 \).
- Q – величина точечного заряда, измеряется в кулонах (Кл).
- r – расстояние от заряда до точки, в которой опр
Роль напряженности электрического поля при взаимодействии с проводниками
Напряженность электрического поля оказывает значительное влияние на проводники, расположенные в его области. Проводники обладают особенностью: при наличии внешнего электрического поля в их объеме возникают индукционные токи, которые действуют в направлении, противоположном приложенному полю, что приводит к перераспределению зарядов внутри проводника.
Рассмотрим, что происходит с проводником в условиях электрического поля. Если поле внешнее, то свободные электроны в проводнике начинают двигаться под действием этого поля, что вызывает образование электрического тока. Напряженность поля пропорциональна силе, с которой оно действует на единичный заряд, а сила поля, в свою очередь, зависит от плотности заряда и свойств самого проводника.
Напряженность электрического поля в проводнике влияет на следующие факторы:
- Перераспределение зарядов: При включении проводника в электрическое поле происходит перераспределение свободных зарядов на его поверхности, что вызывает изменение потенциала внутри проводника.
- Зависимость тока от поля: При постоянной температуре напряженность электрического поля прямо пропорциональна току, который проводник проводит, что описывается законом Ома для одно
Как определить напряженность электрического поля в неоднородных средах?
Напряженность электрического поля в неоднородных средах вычисляют с учетом изменения диэлектрической проницаемости ε и распределения зарядов. Основной метод – решение уравнения Пуассона или Лапласа с граничными условиями, отражающими свойства каждой области.
В неоднородных средах напряженность Е связана с вектором электрической индукции Д через уравнение Д = ε₀εE, где ε – локальная диэлектрическая проницаемость, изменяющаяся по координатам. Для корректного определения Е требуется точное знание распределения ε(x,y,z).
Численные методы, такие как метод конечных элементов или метод конечных разностей, применяют для расчета потенциала φ из уравнения ∇·(ε∇φ) = -ρ/ε₀, где ρ – объемная плотность заряда. Напряженность определяется как E = -∇φ.
Практически измеряют потенциалы в нескольких точках, после чего вычисляют градиенты с помощью численного дифференцирования. Важно учитывать переходные слои и интерфейсы, где ε резко меняется, чтобы избежать ошибок в оценке поля.
Экспериментально используют миниатюрные зонды с высокой пространственной разрешающей способностью, позволяющие локально определить напряженность поля с учетом неоднородностей среды.
Применение концепции напряженности электрического поля в промышленности и технике
В производстве полупроводников напряжённость электрического поля используется для управления диффузией примесей в кристаллической решётке кремния.
Вопрос-ответ:
Что такое величина, которая характеризует напряжённость электрического поля?
Эта величина показывает, насколько сильно электрическое поле действует в данной точке пространства. Она определяет силу, с которой поле влияет на заряды, помещённые в эту точку.
Как измеряется напряжённость электрического поля и в каких единицах выражается?
Напряжённость электрического поля измеряется как отношение силы, действующей на положительный пробный заряд, к величине этого заряда. Единицей измерения является ньютон на кулон (Н/Кл) или вольт на метр (В/м), так как эти единицы связаны между собой.
Почему напряжённость электрического поля является векторной величиной?
Она обладает направлением и величиной, поскольку сила, которую испытывает заряд в поле, всегда имеет определённое направление. Векторная природа позволяет учитывать направление действия поля и суммировать влияния от разных источников.
Какая связь существует между напряжённостью электрического поля и потенциалом в этой точке?
Напряжённость электрического поля связана с изменением потенциала по пространству. Она равна градиенту потенциала с обратным знаком, то есть показывает, как быстро меняется потенциал в конкретном направлении.
Как изменяется напряжённость электрического поля при удалении от заряда, создающего это поле?
При удалении от точечного заряда величина напряжённости уменьшается пропорционально квадрату расстояния. Чем дальше от источника, тем слабее воздействие поля в данной точке.