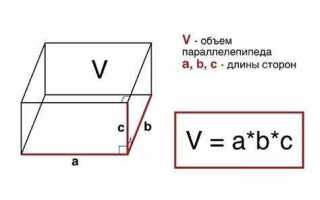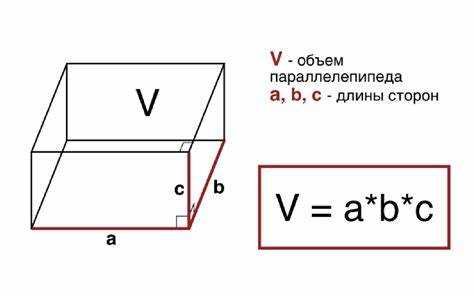
Площадь основания геометрической фигуры можно определить, если известны её объём и высота. Эта задача часто возникает при работе с трёхмерными телами, такими как призмы, цилиндры или параллелепипеды. Ключевая формула: S = V / h, где S – площадь основания, V – объём, h – высота.
Пример: объём прямого цилиндра составляет 314 см³, высота – 10 см. Площадь основания находится делением объёма на высоту: 314 / 10 = 31,4 см². Это значение соответствует площади круга с радиусом, который можно найти отдельно, если потребуется.
Для тел с одинаковыми основаниями, но разной высотой, формула сохраняется. Однако важно учитывать единицы измерения: если объём дан в кубических метрах, а высота в сантиметрах, необходимо привести всё к одной системе. Нарушение этого требования приводит к некорректным результатам.
Формула S = V / h применима только в тех случаях, когда основание перпендикулярно высоте. При наклонных телах или телах с переменной площадью основания использовать её нельзя – потребуется интегральный подход или иные геометрические методы.
В каких случаях можно найти площадь, зная объём и высоту
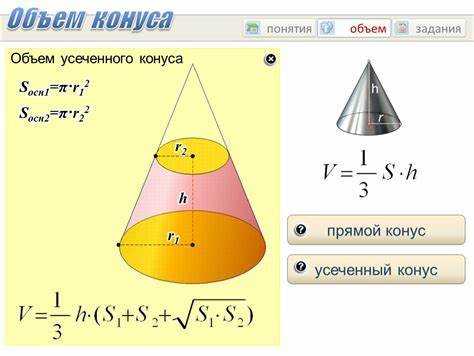
Площадь можно определить по объёму и высоте, если речь идёт о телах с равномерным поперечным сечением по всей высоте. К таким фигурам относятся призмы и цилиндры. Формула применяется следующая: S = V / h, где S – площадь основания, V – объём, h – высота.
Для прямоугольной призмы с известной высотой и объёмом достаточно подставить значения в формулу. Например, если объём составляет 120 м³, а высота – 10 м, то площадь основания: S = 120 / 10 = 12 м².
Аналогично рассчитывается площадь основания у цилиндра, если известен объём и высота. Это допустимо только в случае, когда ось цилиндра перпендикулярна основанию, а высота измеряется вдоль этой оси. При косых цилиндрах формула неприменима без дополнительных преобразований.
Также формула может использоваться при расчётах, связанных с архитектурными или инженерными задачами, где известны геометрические параметры конструкций с постоянным поперечным сечением. При этом важно, чтобы измерения высоты и объёма проводились в согласованных единицах.
Если форма тела неравномерная или сечение меняется по высоте (например, конус или пирамида), прямой расчёт площади через объём и высоту невозможен. В таких случаях требуются другие формулы, учитывающие геометрию фигуры.
Формула площади основания через объём и высоту
Для вычисления площади основания используется соотношение между объёмом и высотой тел с прямолинейной геометрией. Базовая формула:
S = V / h
где S – площадь основания, V – объём, h – высота фигуры. Это равенство применимо к призме, цилиндру и другим телам с постоянным сечением по высоте.
Важно использовать однородные единицы измерения. Если объём задан в кубических метрах, высота тоже должна быть в метрах. При несоответствии единиц результат будет некорректным.
Например, при объёме 12 м³ и высоте 3 м, площадь основания составит: S = 12 / 3 = 4 м².
Формула не применяется к пирамидам и конусам, где объём рассчитывается иначе. Для них требуется учёт коэффициента в формуле объёма.
Как найти площадь основания призмы по известному объёму

Площадь основания призмы определяется через формулу объёма: \( V = S \cdot h \), где \( V \) – объём, \( S \) – площадь основания, \( h \) – высота. Чтобы выразить площадь, достаточно преобразовать формулу: \( S = \frac{V}{h} \).
Если объём равен 240 см³, а высота призмы – 8 см, то площадь основания: \( \frac{240}{8} = 30 \) см².
Высота должна быть перпендикулярна основанию. Её значение должно быть в тех же единицах, что и объём. Например, если объём в кубических метрах, а высота в сантиметрах, нужно привести единицы к общему виду: \( 1\,м = 100\,см \), \( 1\,м³ = 1\,000\,000\,см³ \).
Формула применима для любых призм: прямоугольных, треугольных, многоугольных. Главное – точно определить высоту и объём.
Площадь круга через объём и высоту цилиндра
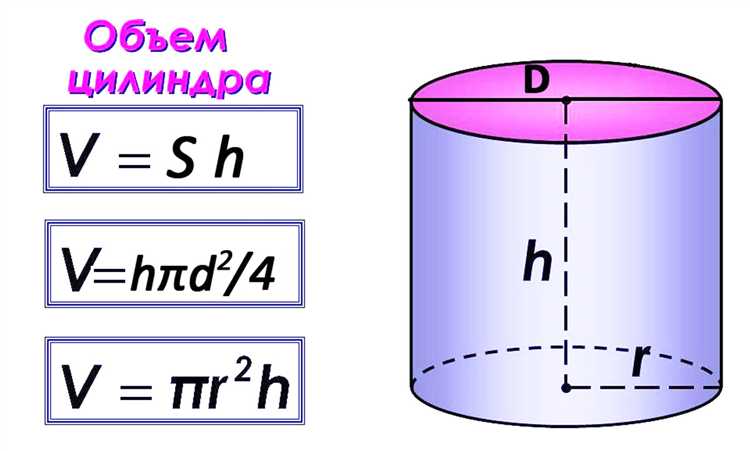
Если известны объём цилиндра и его высота, можно найти площадь основания, то есть площадь круга. Используется формула объёма цилиндра:
V = S × h,
где:
- V – объём цилиндра,
- S – площадь основания (круга),
- h – высота цилиндра.
Выразим площадь круга:
S = V / h
Порядок действий:
- Проверьте, чтобы объём и высота были в одних и тех же единицах (например, см³ и см).
- Разделите объём на высоту.
- Результат – площадь круга в квадратных единицах.
Пример: объём цилиндра 628 см³, высота 8 см.
S = 628 / 8 = 78,5 см²
Как вычислить площадь основания пирамиды при известном объёме
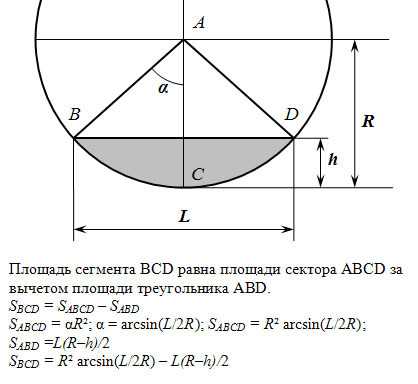
Чтобы найти площадь основания пирамиды, зная её объём, необходимо использовать формулу объёма правильной пирамиды:
V = (S × h) / 3,
где V – объём пирамиды, S – площадь основания, h – высота.
Выразим площадь основания:
S = (3 × V) / h
Подставьте численные значения объёма и высоты в эту формулу. Например, если объём пирамиды составляет 120 кубических сантиметров, а высота равна 10 сантиметрам:
S = (3 × 120) / 10 = 36 см²
Важно: высота должна быть перпендикулярна основанию. Если дана длина бокового ребра или апофема, потребуется сначала вычислить истинную высоту, используя теорему Пифагора.
При работе с произвольными пирамидами с неправильным основанием необходимо уточнить, что используется вертикальная высота, а не наклонная. Без этого результат будет неточным.
Определение площади основания конуса через объём и высоту
Объём конуса рассчитывается по формуле V = (1/3) * Sосн * h, где V – объём, Sосн – площадь основания, h – высота.
Для нахождения площади основания необходимо выразить её из формулы объёма: Sосн = 3V / h.
Подставив известные значения объёма и высоты, выполняют деление произведения объёма на высоту с последующим умножением на 3.
Результат – площадь основания конуса в тех же единицах измерения, что использовались для объёма и высоты.
Важно убедиться, что объём и высота выражены в совместимых единицах (например, объём в кубических метрах, высота в метрах), чтобы итог получился корректным.
Как использовать объём и высоту для расчёта площади сечения
Площадь сечения определяется по формуле:
Площадь сечения = Объём ÷ Высота
Значения объёма и высоты должны быть выражены в согласованных единицах. Если объём задан в кубических метрах (м³), высота – в метрах (м), площадь сечения получится в квадратных метрах (м²).
Например, если объём равен 12 м³, а высота – 3 м, площадь сечения будет:
12 м³ ÷ 3 м = 4 м²
Для точного результата измеряйте высоту по перпендикуляру к сечению. Ошибка в высоте напрямую влияет на точность площади.
Если высота изменяется, площадь сечения можно определить в любой момент, разделив текущий объём на новую высоту. Это актуально при вычислении площади для тел с переменной высотой.
Типичные ошибки при расчёте площади из объёма и высоты
Часто встречаются ошибки, влияющие на точность вычислений при определении площади по объёму и высоте. Их можно разделить на несколько категорий:
- Неправильное понимание формулы. При расчёте площади обычно используется формула
Площадь = Объём / Высота. Ошибки возникают, если под объёмом понимают не полный объём, а часть или наоборот включают лишние элементы. - Единицы измерения. Несоответствие единиц высоты и объёма приводит к неверному результату. Например, объём в кубометрах, а высота в сантиметрах без перевода приведут к искажению значения площади.
- Игнорирование формы объекта. Формула применима к телам с постоянным сечением. Для тел с переменным сечением использование этой формулы приводит к ошибкам.
- Округления на промежуточных этапах. Раннее округление значений объёма или высоты снижает точность итогового результата.
- Недооценка погрешностей измерений. Погрешность высоты или объёма существенно влияет на результат площади. Рекомендуется учитывать точность измерительных инструментов.
Рекомендации по снижению ошибок:
- Проверять, что объём и высота измерены в однородных единицах.
- Использовать точные данные и избегать преждевременного округления.
- При сложной геометрии уточнять, применима ли формула для данного случая.
- В случае сомнений проводить контрольные замеры и сравнивать результаты.
Вопрос-ответ:
Как вычислить площадь основания призмы, если известен её объём и высота?
Чтобы найти площадь основания призмы, нужно разделить её объём на высоту. Формула выглядит так: площадь основания = объём ÷ высота. Это связано с тем, что объём призмы равен произведению площади основания на высоту.
Можно ли определить площадь основания цилиндра по объёму и высоте?
Да, можно. Объём цилиндра равен площади основания, умноженной на высоту. Значит, чтобы найти площадь основания, нужно объём разделить на высоту. Полученное значение будет равно площади круга основания цилиндра.
Какие единицы измерения использовать при расчёте площади через объём и высоту?
Для корректного вычисления необходимо, чтобы объём был в кубических единицах (например, кубических метрах), а высота — в линейных единицах (метрах). Тогда площадь основания получится в квадратных единицах (квадратных метрах). Важно, чтобы все измерения были согласованы по системе единиц.
Что делать, если высота фигуры неизвестна, а нужно найти площадь основания по объёму?
Без информации о высоте вычислить площадь основания невозможно, так как объём связан с площадью основания и высотой через произведение. Для точного расчёта требуется знать высоту или иметь дополнительные данные, позволяющие её определить.
Можно ли использовать формулу площадь = объём ÷ высота для всех трёхмерных фигур?
Эта формула применима к фигурам, у которых объём равен произведению площади основания на высоту, например, к призме или цилиндру. Для фигур с другой структурой объёма, например, конуса или пирамиды, нужно использовать другие формулы, учитывающие особенности их формы.