Сила тока в электрической цепи определяется по формуле I = (E — Uвн)/R, где I – сила тока, E – электродвижущая сила источника, Uвн – падение напряжения на внутреннем сопротивлении, R – сопротивление внешней цепи. Этот расчет позволяет точно определить поведение цепи под нагрузкой.
Если внутреннее сопротивление источника обозначить как r, а общее напряжение как U, то формула переписывается: I = E / (R + r). Это соотношение учитывает влияние внутренних потерь и важно при проектировании источников питания, особенно аккумуляторов и генераторов.
Для измерения ЭДС в реальных условиях используется вольтметр с большим сопротивлением, подключаемый без нагрузки. При подключении нагрузки необходимо учитывать изменение напряжения на клеммах источника. Это позволяет избежать ошибок в расчетах при переменных нагрузках и правильно подобрать параметры компонентов.
Точное определение силы тока важно при расчете тепловых потерь, выборе проводов и защите цепи. Пренебрежение внутренним сопротивлением может привести к перегреву и снижению КПД. Поэтому расчет должен учитывать как номинальные, так и реальные параметры источника питания и нагрузки.
Как найти силу тока через ЭДС и рассчитать параметры
Сила тока I определяется через ЭДС ε по закону Ома для полной цепи: I = ε / (R + r), где R – сопротивление внешней цепи, r – внутреннее сопротивление источника.
Если известны значения ЭДС и сопротивлений, подставьте их в формулу. Например, при ε = 12 В, R = 4 Ом, r = 2 Ом: I = 12 / (4 + 2) = 2 А.
Для расчета падения напряжения на внешнем сопротивлении используйте формулу U = I × R. В приведённом примере: U = 2 × 4 = 8 В.
Напряжение на внутреннем сопротивлении находится как Ur = I × r. Здесь: Ur = 2 × 2 = 4 В.
Проверка: сумма напряжений на R и r должна быть равна ЭДС: 8 В + 4 В = 12 В.
Мощность, потребляемая нагрузкой: P = I² × R. В примере: P = 4 × 4 = 16 Вт.
Мощность, теряемая внутри источника: Pr = I² × r. Здесь: Pr = 4 × 2 = 8 Вт.
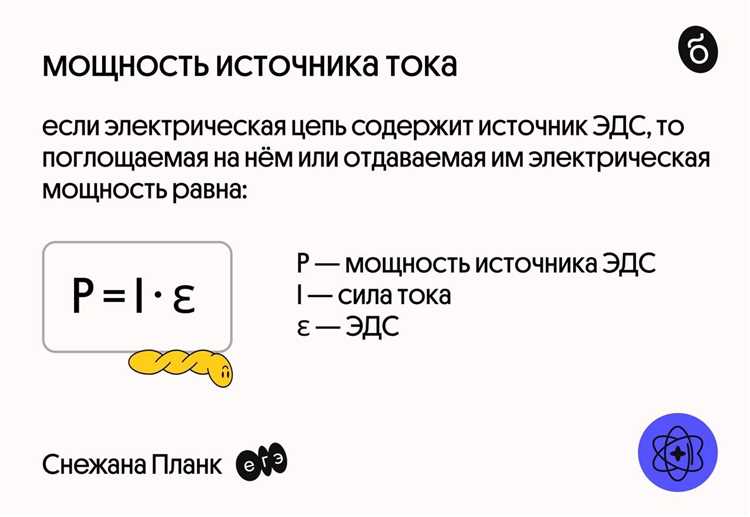
Полная мощность источника: Pобщ = ε × I. В данном случае: Pобщ = 12 × 2 = 24 Вт.
Эти расчёты позволяют определить все ключевые параметры цепи с источником ЭДС и известными сопротивлениями.
Определение ЭДС и внутреннего сопротивления источника
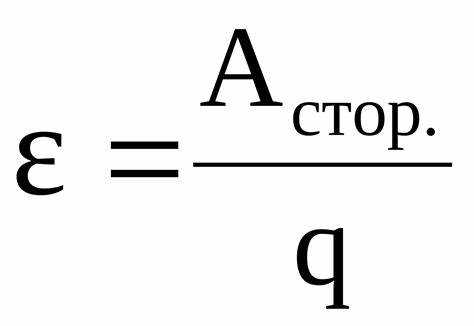
ЭДС (электродвижущая сила) обозначается как 𝑜 и измеряется в вольтах. Это напряжение, создаваемое источником тока в идеальных условиях без нагрузки. Внутреннее сопротивление источника обозначается как r и измеряется в омах. Оба параметра можно определить с использованием закона Ома для полной цепи.
Для измерения требуется амперметр, вольтметр и регулируемая нагрузка. Амперметр подключается последовательно с источником и нагрузкой, вольтметр – параллельно к нагрузке. Проводятся два измерения с разной нагрузкой.
Пусть при первой нагрузке ток I₁, напряжение на клеммах U₁; при второй – I₂ и U₂. Составляются уравнения:
U₁ = ℰ − I₁·r
U₂ = ℰ − I₂·r
Из системы уравнений выражают ЭДС и внутреннее сопротивление:
r = (U₁ − U₂) / (I₂ − I₁)
ℰ = U₁ + I₁·r
При расчёте необходимо использовать одни и те же единицы измерения и учитывать погрешности приборов. Оптимальный диапазон токов – 100–500 мА. Измерения при слишком малых или больших токах снижают точность вычислений.
Расчёт силы тока по закону Ома для полной цепи
Для расчёта силы тока в замкнутой электрической цепи с источником ЭДС используется формула закона Ома для полной цепи:
I = ε / (R + r),
где:
- I – сила тока (в амперах);
- ε – электродвижущая сила источника (в вольтах);
- R – внешнее сопротивление цепи (в омах);
- r – внутреннее сопротивление источника (в омах).
Пример. Дано:
- ε = 12 В;
- R = 8 Ом;
- r = 2 Ом.
Подставляем значения:
I = 12 / (8 + 2) = 12 / 10 = 1.2 А
Сила тока составляет 1.2 ампера. Если необходимо изменить силу тока, можно:
- Увеличить внешнее сопротивление – сила тока уменьшится;
- Уменьшить внутреннее сопротивление источника – сила тока возрастёт;
- Изменить ЭДС – при постоянных сопротивлениях сила тока изменяется пропорционально ЭДС.
Если r пренебрежимо мало по сравнению с R, формула упрощается:
I ≈ ε / R
Этот случай допустим при использовании качественных источников питания с низким внутренним сопротивлением.
Учет внешнего сопротивления при вычислениях

При расчете силы тока через ЭДС необходимо учитывать не только внутреннее сопротивление источника, но и внешнее сопротивление цепи. Оно включает активные элементы: резисторы, проводники, нагрузки.
Сила тока определяется по формуле: I = ε / (Rвн + Rвнеш), где ε – электродвижущая сила источника, Rвн – внутреннее сопротивление, Rвнеш – суммарное внешнее сопротивление.
Пренебрежение внешним сопротивлением приводит к завышенной оценке тока. Например, если Rвн = 0,5 Ом, ε = 12 В, а Rвнеш = 5 Ом, то I = 12 / (0,5 + 5) = 2,18 А. Без учета Rвнеш получилось бы 24 А – результат в десятки раз выше реального.
В схемах с переменными нагрузками Rвнеш пересчитывается каждый раз при изменении конфигурации. При последовательном соединении сопротивления складываются, при параллельном – рассчитываются по формуле 1/Rвнеш = 1/R1 + 1/R2 + … + 1/Rn.
Перед вычислениями следует замерить или рассчитать все внешние сопротивления, включая участки проводников, если их длина значительна. Это особенно важно в низковольтных системах, где влияние сопротивления проводов ощутимо.
Преобразование уравнения при наличии нескольких источников
Если в цепи присутствует несколько источников ЭДС, необходимо учитывать их полярность и внутренние сопротивления. Для составления уравнения применяют метод контурных токов или закон Кирхгофа. При этом важно правильно выбрать направление обхода контура и учитывать знак каждого элемента.
При наличии двух и более источников ЭДС в одном контуре уравнение имеет вид:
∑ЭДС — ∑IR = 0
Где ∑ЭДС – алгебраическая сумма всех источников ЭДС с учетом направления, ∑IR – сумма падений напряжения на резисторах, включая внутренние сопротивления источников. Если направление обхода совпадает с направлением ЭДС, то ЭДС берется со знаком «+», если противоположно – со знаком «−».
Пример: в контуре находятся два источника ЭДС ε₁ = 12 В и ε₂ = 5 В (направленные в одну сторону), внутренние сопротивления r₁ = 1 Ом и r₂ = 0.5 Ом, внешний резистор R = 3 Ом. Тогда уравнение примет вид:
ε₁ — Ir₁ + ε₂ — Ir₂ — IR = 0
Объединяем:
(ε₁ + ε₂) = I(r₁ + r₂ + R)
Подставляем значения:
12 + 5 = I(1 + 0.5 + 3)
17 = I × 4.5
I = 3.78 А
Если один из источников направлен противоположно, его ЭДС берется с отрицательным знаком. Такой подход позволяет корректно рассчитать ток даже при сложной структуре цепи.
Примеры расчёта силы тока в разветвлённой цепи

Рассмотрим цепь с двумя параллельными ветвями, питаемую источником ЭДС 12 В и внутренним сопротивлением 1 Ом. Первая ветвь содержит сопротивление 4 Ом, вторая – 6 Ом.
Для начала определим эквивалентное сопротивление ветвей параллельно: R_экв = (R1 * R2) / (R1 + R2) = (4 * 6) / (4 + 6) = 24 / 10 = 2,4 Ом.
Общее сопротивление цепи с учётом внутреннего сопротивления источника: R_общ = R_внутр + R_экв = 1 + 2,4 = 3,4 Ом.
Сила тока в цепи: I_общ = ЭДС / R_общ = 12 / 3,4 ≈ 3,53 А.
Ток в каждой ветви рассчитывается по закону Ома с учётом напряжения на параллельных ветвях, равного напряжению на R_экв. Напряжение на параллельных ветвях: U_ветв = ЭДС — I_общ * R_внутр = 12 — 3,53 * 1 = 8,47 В.
Ток в первой ветви: I1 = U_ветв / R1 = 8,47 / 4 ≈ 2,12 А.
Ток во второй ветви: I2 = U_ветв / R2 = 8,47 / 6 ≈ 1,41 А.
Проверка: сумма токов ветвей I1 + I2 = 2,12 + 1,41 = 3,53 А, совпадает с общим током.
В другом примере с тремя ветвями 2 Ом, 3 Ом и 6 Ом, при ЭДС 18 В и внутреннем сопротивлении 0,5 Ом:
R_экв = 1 / (1/2 + 1/3 + 1/6) = 1 Ом.
R_общ = 0,5 + 1 = 1,5 Ом.
I_общ = 18 / 1,5 = 12 А.
U_ветв = 18 — 12 * 0,5 = 12 В.
Токи в ветвях: I1 = 12 / 2 = 6 А, I2 = 12 / 3 = 4 А, I3 = 12 / 6 = 2 А.
Сумма I1 + I2 + I3 = 12 А, совпадает с общим током.
Проверка результатов с использованием мощности и закона сохранения энергии
После вычисления силы тока через ЭДС необходимо проверить корректность результата с помощью мощности и закона сохранения энергии. Мощность источника равна произведению ЭДС на силу тока: P = \mathcal{E} \cdot I. Мощность, выделяемая на внешних и внутренних сопротивлениях цепи, должна равняться мощности источника с учетом потерь.
Расчет мощности на резисторе производится по формуле P = I^2 R, где R – сопротивление резистора, а I – найденная сила тока. Внутренние потери источника рассчитываются аналогично: P_{внутр} = I^2 r, где r – внутреннее сопротивление.
Сумма мощностей на всех элементах цепи должна совпадать с полной мощностью источника: \mathcal{E} I = I^2 R + I^2 r. Если наблюдается расхождение, следует проверить правильность вычислений силы тока и параметров сопротивлений.
Таким образом, контроль через мощность позволяет выявить ошибки и подтвердить соответствие результатов закону сохранения энергии, исключая некорректные данные.
Вопрос-ответ:
Как рассчитать силу тока в цепи, если известна ЭДС и сопротивление?
Для нахождения силы тока в цепи с заданной электродвижущей силой (ЭДС) и сопротивлением используется закон Ома. Нужно разделить значение ЭДС на общее сопротивление цепи. Формула выглядит так: I = E / R, где I — сила тока, E — ЭДС, R — сопротивление. Этот расчет позволяет определить, какой ток будет протекать в цепи при заданных параметрах.
Что делать, если в цепи несколько источников ЭДС и разных сопротивлений?
Когда в цепи несколько источников ЭДС и сопротивлений, сначала нужно определить, как они соединены — последовательно или параллельно. Для последовательного соединения суммируются все ЭДС и сопротивления: общая ЭДС равна сумме всех ЭДС с учётом направления, а сопротивления складываются. Для параллельного соединения рассчитываются эквивалентные параметры по специальным формулам. После определения эквивалентной ЭДС и сопротивления можно найти силу тока, разделив общую ЭДС на общее сопротивление.
Как учесть внутреннее сопротивление источника при расчёте силы тока?
Внутреннее сопротивление источника снижает напряжение, доступное для внешней цепи. Чтобы учесть его, внутреннее сопротивление добавляют к сопротивлению внешней цепи. Таким образом, общая величина сопротивления — это сумма внутреннего сопротивления источника и сопротивления нагрузки. После этого сила тока вычисляется по формуле I = E / (R + r), где r — внутреннее сопротивление, а R — сопротивление внешней цепи. Такой подход позволяет получить более точное значение тока.
Почему при расчёте силы тока нельзя просто использовать только значение ЭДС без учёта сопротивления?
ЭДС показывает максимальное напряжение, которое может создать источник, но не учитывает сопротивление цепи, которое ограничивает ток. Если не брать в расчёт сопротивление, полученный ток будет бесконечно большим, что не соответствует реальности. Сопротивление — это препятствие для протекания электричества, и его величина определяет, насколько сильным будет ток. Поэтому без сопротивления формула для силы тока не применима, и расчет будет некорректным.