Как рассчитать ток в трехфазной сети

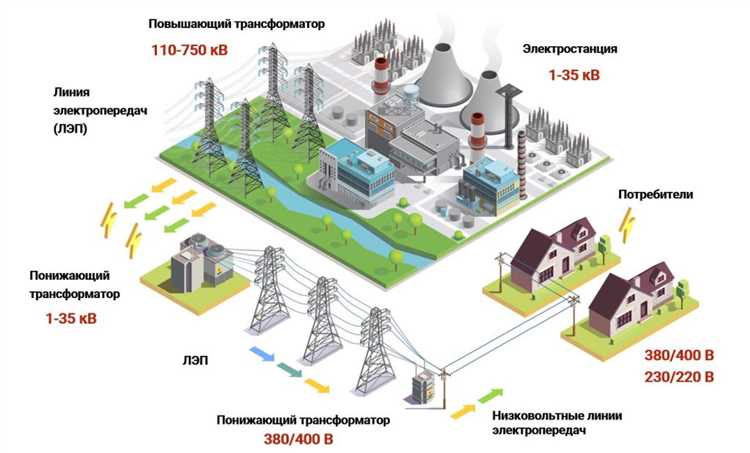
Ток в трехфазной сети напрямую зависит от типа соединения, нагрузки и величины линейного напряжения. Для симметричных нагрузок расчет упрощается: при соединении по схеме звезда фазный ток определяется делением активной или полной мощности на произведение корня из трёх и линейного напряжения. При соединении по схеме треугольник фазный ток равен току в нагрузке, а линейный – больше в √3 раза. Несимметричные и смешанные нагрузки требуют пофазного анализа.

В промышленной практике используются выражения: I = P / (√3 × U × cos φ) для активной мощности и I = S / (√3 × U) для полной. Здесь P – активная мощность в ваттах, S – полная мощность в вольт-амперах, U – линейное напряжение, cos φ – коэффициент мощности. Понимание назначения этих параметров критично при проектировании сетей, где важна корректная нагрузка на автоматические выключатели и трансформаторы.

Расчеты должны учитывать фазовый дисбаланс, особенно в сетях с неравномерно распределенными потребителями. Для оценки тока нейтрали в таких случаях применяются векторные диаграммы и методы симметричных составляющих. Игнорирование фазового перекоса может привести к локальному перегреву и преждевременному выходу оборудования из строя.

Рекомендуется выполнять расчеты в программной среде, способной учитывать все режимные параметры – это минимизирует вероятность ошибки. При этом важно контролировать значения не только тока, но и реактивной мощности, особенно в сетях с большим количеством электродвигателей и преобразовательной техники.

Определение фазного и линейного напряжения для различных схем подключения

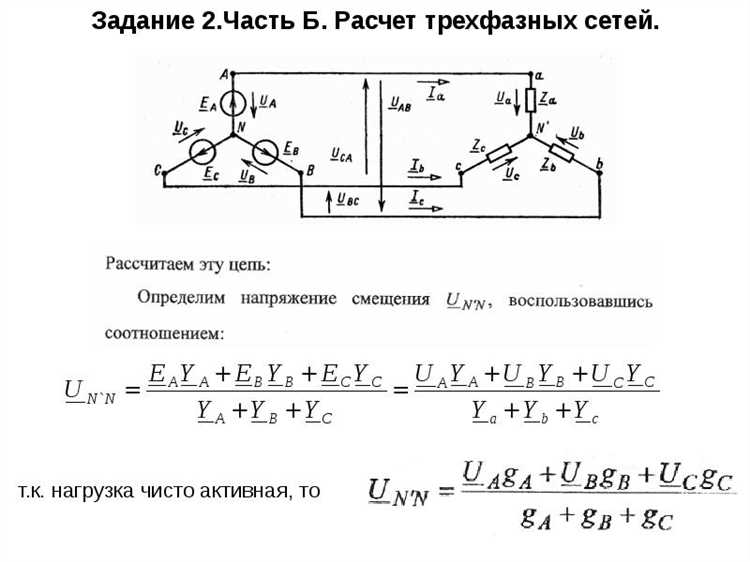
В трехфазных системах используются две основные схемы подключения: «звезда» (Y) и «треугольник» (Δ). Для точного расчета токов необходимо корректно определить тип напряжения: фазное или линейное.

Схема звезда (Y): каждая фаза подключается между одной линейной жилой и нейтралью. Напряжение между фазой и нейтралью – фазное. Величина фазного напряжения составляет 220 В (в сетях 380/220 В).
Линейное напряжение в «звезде» измеряется между двумя фазами. Оно превышает фазное в √3 раза. Формула: U_л = √3 × U_ф. Для стандартной сети: U_л = √3 × 220 ≈ 380 В.

Схема треугольник (Δ): фазы соединяются последовательно в замкнутый контур, без нейтрали. Подключение происходит между двумя линейными проводами. В этой схеме линейное и фазное напряжения равны: U_л = U_ф.

При расчете токов важно не путать значения. Например, в схеме «звезда» при использовании фазного напряжения необходимо учитывать, что ток в фазе равен току в линии: I_ф = I_л. В «треугольнике» наоборот: I_л = √3 × I_ф.

Выбор между схемами зависит от требований к напряжению, наличия нейтрали и типа нагрузки. При однофазной нагрузке с обязательным подключением к нейтрали возможна только схема «звезда». Для мощных трехфазных двигателей без нейтрали – схема «треугольник».

Перед расчетами всегда проверяйте схему подключения: от этого зависит правильность подставляемых в формулы значений напряжения и тока.

Расчет тока в звезде с известной активной и реактивной мощностью нагрузки

Для расчета линейного тока в трехфазной сети с соединением нагрузки по схеме «звезда» при известных активной (P) и реактивной (Q) мощностях используется мощность полной нагрузки (S), которая определяется как:

S = √(P² + Q²)

Зная линейное напряжение (U_л), ток в одной фазе можно найти по формуле:

I = S / (√3 × U_л)

Если напряжение фазное (U_ф) известно, то формула упрощается:

I = S / (3 × U_ф)

Для определения угла φ между током и напряжением используется отношение активной и полной мощности:

cosφ = P / S

Это значение необходимо при проверке соответствия нагрузке допустимых параметров электросети и обеспечения минимальных потерь.

Пример: при P = 9 кВт, Q = 12 кВАр и линейном напряжении 400 В:

S = √(9² + 12²) = 15 кВА
I = 15000 / (√3 × 400) ≈ 21.65 А
cosφ = 9 / 15 = 0.6

Результат – линейный ток 21.65 А, угол сдвига фаз около 53.13° (арccos 0.6). Такой расчет необходим при проектировании и подборе оборудования: автоматов, кабелей, трансформаторов.

Расчет тока в треугольнике при заданной полной мощности

В трехфазной электрической сети расчет тока при заданной полной мощности в режиме треугольника (или соединении «Delta») имеет особенности, которые важно учитывать для правильного проектирования и эксплуатации оборудования.

Для начала, полная мощность \(S\) в трехфазной сети определяется по формуле:

S = √3 × U × I × cos(φ),

где:

S – полная мощность, ВА;
U – линейное напряжение, В;
I – линейный ток, А;
cos(φ) – коэффициент мощности.

Для треугольного соединения коэффициент мощности часто считается равным 1, если нет значительных потерь или других факторов. Тогда формула для расчета тока упрощается:

I = S / (√3 × U)

Где:

I – ток в каждой фазе (в амперах);
S – полная мощность, ВА;
U – линейное напряжение сети, В.

Таким образом, зная полную мощность сети и линейное напряжение, можно вычислить ток, протекающий через каждую фазу.

Если необходимо рассчитать фазный ток, то он будет отличаться от линейного. Для треугольного соединения фазный ток можно вычислить по следующей формуле:

I_ф = I / √3

Где:

I_ф – фазный ток, А;
I – линейный ток, А.

Рассмотрим пример. Пусть задано следующее:

Полная мощность \(S = 30 \, \text{кВА}\);
Линейное напряжение \(U = 400 \, \text{В}\);
Коэффициент мощности \(cos(φ) = 1\).

Тогда, линейный ток можно вычислить по формуле:

I = 30,000 / (√3 × 400) ≈ 43.3 \, \text{А}

Далее, для фазного тока:

I_ф = 43.3 / √3 ≈ 25.0 \, \text{А}

Этот расчет дает возможность правильно выбрать проводку и оборудование для безопасной эксплуатации трехфазной сети в треугольном соединении.

При проектировании важно помнить, что расчет мощности и тока не всегда ограничивается простыми формулами. Нужно учитывать сопротивление линий, возможные потери и специфические параметры устройства, например, трансформаторов или двигателей, в которых могут быть дополнительные коэффициенты. Точные значения могут изменяться в зависимости от факторов, таких как частота сети или температурные условия.

Учет сдвига фаз при расчете тока в трехфазной цепи с косинусом φ

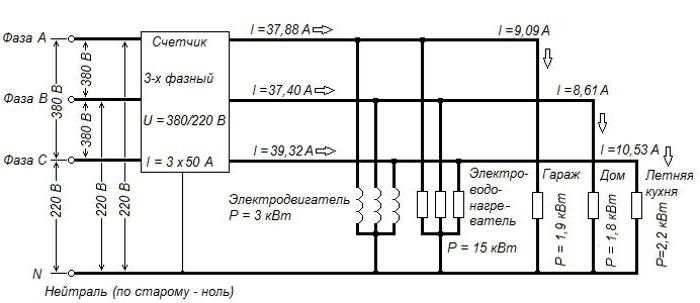
При расчете тока в трехфазной электрической сети необходимо учитывать сдвиг фаз между напряжениями и токами. Этот сдвиг влияет на реальную мощность, потребляемую устройствами, и напрямую зависит от коэффициента мощности, определяемого через косинус угла фазового сдвига (cos φ). Для правильного расчета тока важно понимать, как этот сдвиг влияет на характеристики цепи.

Для цепи с симметричными нагрузками, если нагрузка является индуктивной или емкостной, фазовый сдвиг между током и напряжением не равен нулю. В этом случае используется формула для расчета тока с учетом косинуса φ: I = \frac{P}{\sqrt{3} \cdot U \cdot cos φ}, где:

I – ток в одной фазе;
P – активная мощность;
U – фазное напряжение;
cos φ – коэффициент мощности.

Если косинус φ меньше единицы, то ток в цепи будет выше, чем при cos φ = 1. Это важно учитывать при проектировании и расчетах, поскольку повышение потребляемого тока может привести к перегрузке элементов сети.

Важно помнить, что сдвиг фаз также влияет на реактивную мощность. В случае сильно индуктивной нагрузки (например, в двигателях) cos φ может быть существенно меньше 1, что увеличивает нагрузку на систему. В таких случаях для корректного выбора кабелей и защитных устройств следует учитывать как активную, так и реактивную мощность.

Если сеть работает с асимметричной нагрузкой, то сдвиг фаз в каждой фазе может различаться, что требует индивидуального расчета тока для каждой из фаз. В таких ситуациях общее значение тока в цепи можно найти, используя формулу для неконтролируемых нагрузок, с учетом поправки на несимметричность и дополнительные потери.

Для получения точных значений тока в трехфазной сети всегда следует учитывать не только значение фазового угла, но и тип нагрузки, коэффициент мощности и возможные изменения в рабочем режиме системы.

Примеры расчета тока при несимметричной нагрузке

При несимметричной нагрузке в трехфазной сети, токи в фазах будут различаться по величине. Для расчета тока в каждом из фазовых проводников необходимо учитывать параметры системы и тип нагрузки. Рассмотрим несколько примеров.

1. Если нагрузка представляет собой последовательное соединение резистора и индуктивности, то ток в каждой фазе зависит от сопротивления и реактивного сопротивления, а также от угла сдвига фазы тока относительно напряжения. Например, если сопротивление в одной фазе составляет 20 Ом, а индуктивность дает реактивное сопротивление 15 Ом, то ток в этой фазе можно рассчитать как:

I = U / √(R² + X²),

где U – фазное напряжение, R – активное сопротивление, X – реактивное сопротивление.

2. Для симметричной нагрузки, например, при подключении балластных сопротивлений на каждой фазе, токи в фазах будут равны. Однако если в одной фазе добавлена дополнительная индуктивность, это приведет к изменению тока в этой фазе. Допустим, в одной фазе сопротивление увеличено до 30 Ом, а в другой – уменьшено до 10 Ом. В этом случае токи будут отличаться, и его расчет можно выполнить по аналогичной формуле с учетом нового сопротивления.

3. При наличии однофазных приборов или несимметричных резистивных нагрузок в одной или нескольких фазах, расчет тока в этих фазах следует делать с учетом суммарной нагрузки на каждую фазу. Например, если в первой фазе нагрузка составляет 5 кВт, а в остальных двух фазах – по 2 кВт, то ток в каждой фазе можно вычислить по формуле:

I = P / (√3 * U),

где P – мощность нагрузки, U – фазное напряжение.

4. В случае наличия активной и реактивной мощности на каждой из фаз, необходимо учитывать коэффициент мощности для точного расчета. Если в одной фазе нагрузка состоит из активной мощности 4 кВт и реактивной 2 кВт, то ток можно рассчитать, используя комплексную мощность:

S = √(P² + Q²),

где P – активная мощность, Q – реактивная мощность. Ток в фазе будет:

I = S / (√3 * U).

Все эти примеры показывают, как важно учитывать не только величину нагрузки, но и ее характеристики, такие как сопротивление, реактивность и мощность для правильного расчета тока в трехфазной сети при несимметричной нагрузке.

Выбор сечения кабеля по рассчитанному току и допустимому нагреву

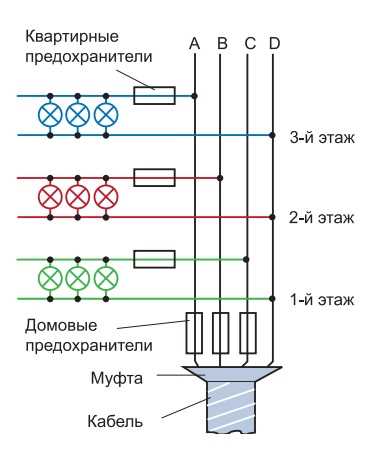
Определение сечения кабеля начинается с точного значения рабочего тока, рассчитанного для конкретной трехфазной нагрузки. Для обеспечения безопасности и долговечности проводника необходимо учитывать максимально допустимую температуру нагрева изоляции, которая напрямую влияет на его токовую нагрузку.

Расчетная токовая нагрузка определяется по формуле для трехфазной сети: I = P / (√3 × U × cos φ), где P – активная мощность нагрузки, U – линейное напряжение, cos φ – коэффициент мощности. Полученный ток служит базой для выбора сечения.

Следующий этап – сверка рассчитанного тока с допустимым током кабеля, указанным в технической документации производителя. Значение зависит от материала жилы (медь или алюминий), типа изоляции и условий прокладки (воздух, грунт, труба). Например, медный кабель с изоляцией из ПВХ при прокладке в воздухе при температуре до 30°C выдерживает ток до 25 А для сечения 2,5 мм², а при прокладке в грунте ток снижается до 21 А.

Если расчетный ток превышает нормативный, выбирают кабель с большим сечением. При этом следует учитывать, что увеличение сечения не всегда линейно повышает допустимый ток из-за тепловых условий монтажа и группового прокладывания кабелей, что требует дополнительных корректировок.

Для оценки допустимого нагрева важно учитывать максимально допустимую температуру изоляции – чаще всего 70°C для ПВХ и 90°C для сшитого полиэтилена (СИП). Превышение температуры снижает ресурс кабеля и увеличивает риск аварий.

Рекомендуется применять коэффициенты корректировки для условий эксплуатации: например, при температуре окружающей среды выше 30°C токовую нагрузку снижают на 10–15%. При прокладке нескольких кабелей в одной канаве применяют коэффициент уменьшения до 0,7.

Выбор сечения следует производить с запасом не менее 10–15% к расчетному току, чтобы обеспечить устойчивость к перегрузкам и избежать критического нагрева. Пренебрежение этим правилом приводит к ускоренному старению изоляции и возможному выходу из строя электрооборудования.

Вопрос-ответ:

Что такое трехфазная электрическая сеть и почему она используется?

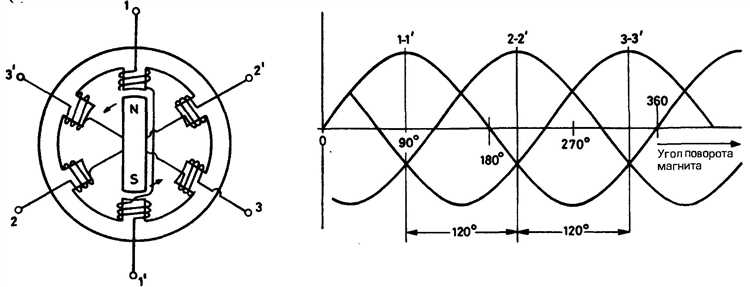
Трехфазная электрическая сеть представляет собой систему, в которой используются три фазы тока, сдвинутые друг относительно друга на 120 градусов. Такая структура позволяет более равномерно распределять нагрузку, повышая эффективность передачи электроэнергии. Трехфазные системы предпочтительны в промышленности, так как обеспечивают более высокую мощность и стабильную работу оборудования по сравнению с однофазными сетями.

Что такое коэффициент мощности (cosφ) и как он влияет на расчет тока?

Коэффициент мощности (cosφ) — это отношение активной мощности (потребляемой энергией) к полной мощности (совокупности активной и реактивной). Этот коэффициент показывает, насколько эффективно используется энергия в электрической системе. Если cosφ близок к единице, система работает эффективно, а если меньше, это означает наличие реактивной мощности, что снижает общую эффективность. В расчетах тока более высокие значения cosφ приводят к меньшему току при одинаковой мощности.

Как правильно рассчитать ток в трехфазной сети с подключением к ней разных типов нагрузки?

Если нагрузка на каждой из фаз разная, то используется метод расчета для несимметричных нагрузок. В этом случае необходимо учитывать индивидуальные параметры каждой фазы, включая фазовые углы и величины токов. Для расчета тока в таких системах могут быть использованы векторные диаграммы и методы анализа с использованием комплексных чисел. Важно учитывать, что несбалансированные нагрузки могут привести к повышенному тепловыделению и излишним потерям в проводах.

Какие факторы могут повлиять на точность расчета тока в трехфазной сети?

На точность расчета тока могут влиять несколько факторов. Во-первых, это качество измерений напряжения и мощности, а также точность определения коэффициента мощности (cosφ). Во-вторых, при наличии несимметричных нагрузок важно правильно учитывать фазовые сдвиги и разницу в нагрузках на разных фазах. Технические особенности оборудования и проводки, а также воздействие внешних факторов, таких как температура, также могут повлиять на результаты расчета.