
Соотношение трех к четырем обозначается как 3:4 и отражает количественное отношение двух величин. Это значит, что на каждые 3 единицы одной части приходится 4 единицы другой. Например, если в классе 3 мальчика на 4 девочки, общее число учеников будет 7, и пропорция сохранится при любом кратном увеличении.
Для практического понимания достаточно представить ситуации, где количество элементов делится на части в этом отношении. Если у вас 21 яблоко, разделите его на части 3 и 4 – получится 9 и 12 яблок соответственно. Умножая или деля обе части на одно и то же число, вы сохраняете исходное соотношение.
При решении задач с такими пропорциями полезно использовать метод «единицы», когда общая сумма частей разбивается на одинаковые доли. Так, сумма частей 3 и 4 равна 7, и одна доля – это одна седьмая от общего количества. Этот подход упрощает расчет и делает понятным любое преобразование чисел в заданном соотношении.
Что значит соотношение 3 к 4 на практике

Соотношение 3 к 4 отражает отношение двух величин, где первая часть равна 3, а вторая – 4. На практике это значит, что на каждые 3 единицы одной величины приходится 4 единицы другой.
Примеры и рекомендации для понимания и применения соотношения 3:4:
- Если у вас есть 3 красных шарика и 4 синих, всего 7 шариков. Доля красных – 3/7, синих – 4/7.
- При делении бюджета на проект, где отдел А получает 3 части, а отдел B – 4 части, на каждый 7-й рубль 3 пойдут отделу А, 4 – отделу B.
- Для приготовления смеси из двух ингредиентов: если нужно 3 части воды и 4 части сока, то при 300 мл воды потребуется 400 мл сока.
- В строительстве, при заданном соотношении длины и ширины комнаты 3:4, если длина 3 метра, ширина будет 4 метра. Для масштабирования умножайте обе части пропорционально.
Чтобы применить соотношение 3 к 4 в любых расчетах:
- Определите сумму частей (3 + 4 = 7).
- Разделите общую величину на 7, чтобы найти стоимость одной части.
- Умножьте стоимость одной части на 3 и 4 для соответствующих значений.
Такой подход гарантирует точное распределение ресурсов, размеров или количеств в заданной пропорции 3 к 4.
Как сравнивать части при соотношении 3:4
Соотношение 3:4 означает, что одна часть равна трем единицам, а вторая – четырём. Для сравнения частей нужно привести их к общему измерению. Например, если в первом наборе 3 яблока, а во втором – 4, то количество фруктов во втором на 1 больше.
При решении задач разделите общее количество на сумму частей (3 + 4 = 7). Каждая часть тогда соответствует одной седьмой доле. Для первой части это 3/7, для второй – 4/7. Это позволяет определить точную величину каждой части в общем объёме.
Чтобы сравнить части в других величинах, умножьте каждую часть на единичный размер. Например, если общий вес равен 70 кг, первая часть весит 30 кг (70 × 3/7), вторая – 40 кг (70 × 4/7). Таким образом легко определить абсолютные величины и проверить правильность пропорций.
Если данные представлены в процентах, часть 3 соответствует 42,86%, а часть 4 – 57,14%. Это полезно для оценки долей в процентах без округления.
Сравнивая части, учитывайте контекст задачи. Если измерения разные, приведите их к одной системе, чтобы избежать ошибок. Подход с делением на сумму частей и умножением на единицу подходит для любых количественных показателей, будь то длина, масса или время.
Пример деления пиццы в пропорции 3 к 4
Представим, что у вас есть одна пицца, которую нужно разделить между двумя группами людей в соотношении 3 к 4. Это значит, что на каждую часть первой группы приходится 3 части пиццы, а на вторую – 4 части.
Для удобства разобьем пиццу на 7 равных кусочков – сумма частей 3 и 4. Первая группа получает 3 куска, вторая – 4 куска. Если пицца весит 700 грамм, тогда первая группа получает 300 грамм, вторая – 400 грамм.
При практическом разделении пиццы учитывайте, что куски должны быть равны по размеру. Используйте нож с делениями или заранее нарезанную пиццу на 7 равных частей. Если пицца круглой формы, разделите ее на 7 секторов одинакового угла.
Если количество пицц больше, например 2 пиццы, умножьте общее число кусков на 2 – получится 14 кусков, распределите 6 кусков первой группе и 8 второй. Пропорция сохраняется независимо от общего количества.
Как использовать соотношение 3 к 4 при смешивании красок
Соотношение 3 к 4 при смешивании красок означает, что на каждые 3 части одного цвета добавляют 4 части другого. Это позволяет добиться точного оттенка и контролировать интенсивность цвета.
Например, если вы хотите получить мягкий фиолетовый, смешайте 3 части красного с 4 частями синего. Для точности используйте мерные стаканчики или шприцы, чтобы избежать погрешностей.
Если базовый цвет слишком насыщенный, уменьшите количество красок, сохраняя пропорцию 3:4. Например, вместо 300 мл и 400 мл возьмите 30 мл и 40 мл, сохранив баланс оттенка.
При подготовке смеси сначала отмерьте 3 части первого цвета, затем добавьте 4 части второго, тщательно перемешивая. Проверяйте цвет на небольшом участке, так как на разных поверхностях оттенок может меняться.
Для корректировки оттенка увеличивайте количество одной из красок, соблюдая начальную пропорцию, чтобы избежать резких изменений. Например, добавив 6 частей красного и 8 частей синего, получите более насыщенный оттенок с тем же балансом.
Используйте соотношение 3 к 4 при создании градиентов или при наложении нескольких слоев – это поможет сохранить гармонию цвета и равномерность переходов.
Рассчитываем количество ингредиентов по пропорции 3 к 4
Пропорция 3 к 4 означает, что на каждые 3 части одного ингредиента приходится 4 части другого. Чтобы правильно рассчитать количество ингредиентов, нужно исходить из общего объема или заданного количества одного из компонентов.
- Определите известное количество одного из ингредиентов. Например, если у вас есть 300 г первого компонента, это будет 3 части.
- Вычислите вес одной части: 300 г ÷ 3 = 100 г.
- Рассчитайте количество второго ингредиента, умножив вес одной части на 4: 100 г × 4 = 400 г.
Если необходимо получить суммарное количество смеси, сложите рассчитанные части: 300 г + 400 г = 700 г.
- Для увеличения порции умножьте обе части на одинаковый коэффициент. Например, при коэффициенте 2: 3 × 2 = 6 частей, 4 × 2 = 8 частей.
- Если задан общий вес смеси, разделите его на сумму частей (3 + 4 = 7), затем умножьте на каждую часть: при 700 г смеси одна часть – 100 г, первый ингредиент – 300 г, второй – 400 г.
- Для точных расчетов используйте калькулятор или электронные таблицы, чтобы избежать ошибок в дробных значениях.
Такая методика позволяет быстро и точно определять нужное количество компонентов при работе с пропорциями 3 к 4, обеспечивая правильное соотношение и стабильный результат.
Построение прямоугольника с отношением сторон 3 к 4

Для создания прямоугольника с соотношением сторон 3 к 4 начните с выбора одной из сторон. Пусть длина короткой стороны равна 3 единицы. Тогда длинная сторона должна быть 4 единицы.
Если работать с конкретными размерами, например, кратными 3 и 4, легко масштабировать фигуру. Например, при увеличении короткой стороны до 6 см, длинная автоматически станет 8 см, сохраняя пропорции.
Для точного построения можно использовать линейку и угольник. Отметьте на бумаге отрезок в 3 см, затем от одного из его концов проведите перпендикуляр длиной 4 см. Соедините свободные концы этих отрезков – полученный четырехугольник будет прямоугольником с требуемым соотношением.
При необходимости масштабировать прямоугольник, умножайте обе стороны на одно и то же число, например, на 2 или 5, чтобы сохранить соотношение 3 к 4 без искажений.
В чертежных программах или при цифровом моделировании установите размеры сторон по формуле: ширина = 3 × k, высота = 4 × k, где k – масштабный коэффициент.
Перевод соотношения 3 к 4 в проценты и дроби
Соотношение 3 к 4 обозначает отношение двух чисел: 3 и 4. Чтобы представить его в виде дроби, нужно записать первую часть в числитель, а вторую – в знаменатель. Получается дробь 3/4.
Для перевода этой дроби в проценты достаточно разделить числитель на знаменатель и умножить на 100%. Делим 3 на 4, получаем 0,75. Умножаем 0,75 на 100%, итог – 75%.
Таким образом, соотношение 3:4 эквивалентно дроби 3/4 и процентному значению 75%. Этот перевод позволяет использовать соотношение в различных расчетах и сравнениях, например, при вычислении частей целого или распределении ресурсов.
Практическое применение соотношения 3 к 4 в повседневных задачах
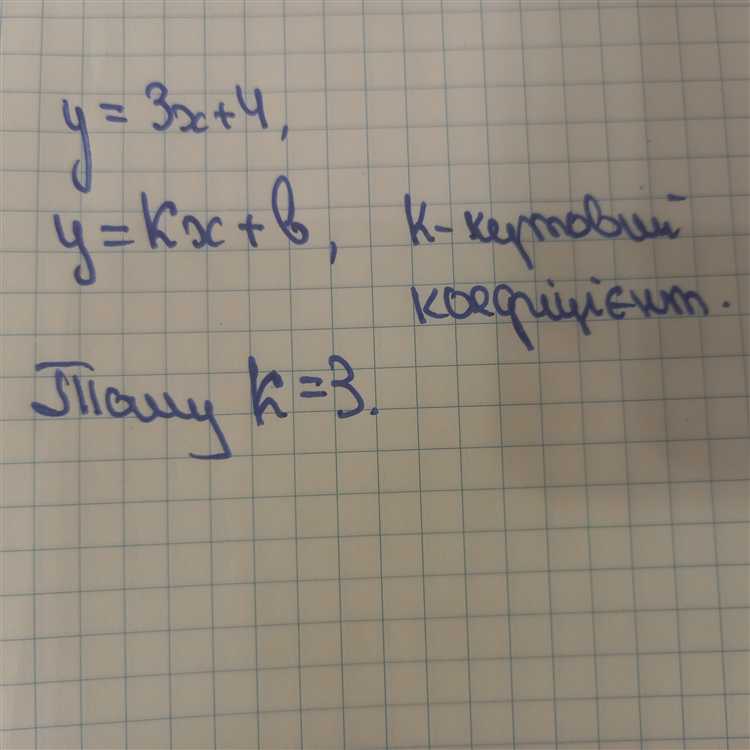
Соотношение 3 к 4 часто встречается при решении бытовых и рабочих задач. Например, при приготовлении пищи рецепт требует смешать ингредиенты в пропорции 3 части муки к 4 частям жидкости. Если нужно приготовить тесто с 300 граммами муки, объем жидкости рассчитывается как 300 × (4/3) = 400 грамм.
При создании мебели или ремонте соотношение 3:4 помогает подобрать размеры деталей. Если ширина полки 60 см, то оптимальная глубина при сохранении пропорций составит 60 × (4/3) = 80 см. Такой расчет улучшит функциональность и внешний вид изделия.
В строительстве при заливке фундамента часто применяют бетонную смесь в пропорции 3 части песка к 4 частям цемента. Для заливки участка площадью 12 м² и толщиной 0,1 м потребуется 3,6 м³ смеси, из которых песка будет 3,6 × (3/7) ≈ 1,54 м³, а цемента 3,6 × (4/7) ≈ 2,06 м³.
При планировании бюджета, если три категории расходов составляют 3 к 4 по отношению к доходам, и доход равен 40 000 рублей, расходы на эти категории можно рассчитать как 40 000 × (3/7) ≈ 17 143 рублей. Это помогает контролировать финансовые потоки и не выходить за рамки.
Для масштабирования чертежей или изображений пропорция 3 к 4 сохраняет корректные размеры. Если исходная длина объекта 9 см, ширина должна быть 9 × (4/3) = 12 см, чтобы не искажать пропорции и сохранить точность.






