
Точная оценка мощности, потребляемой электрической нагрузкой, необходима для правильного выбора оборудования, защиты цепей и минимизации потерь. В электротехнике применяются различные формулы в зависимости от типа тока и характера нагрузки – активной, реактивной или полной.
Для расчета активной мощности в цепи постоянного тока используется формула P = U × I, где U – напряжение в вольтах, I – ток в амперах, P – мощность в ваттах. Эта формула применима к нагрузкам без реактивной составляющей, например, к резистивным элементам.
В цепях переменного тока активная мощность рассчитывается по формуле P = U × I × cos(φ), где cos(φ) – коэффициент мощности, отражающий фазовый сдвиг между током и напряжением. Он особенно важен при работе с индуктивными или ёмкостными нагрузками, такими как электродвигатели или трансформаторы.
Полная мощность определяется выражением S = U × I и измеряется в вольт-амперах (ВА), а реактивная мощность – по формуле Q = U × I × sin(φ), в вар (вольт-амперах реактивных). Эти параметры учитываются при проектировании источников питания и выборе кабелей с достаточным сечением.
При расчётах в трёхфазных системах применяются модифицированные формулы, например, P = √3 × Uф × I × cos(φ) для активной мощности, где Uф – фазное напряжение. Ошибки при вычислениях могут привести к перегреву оборудования, снижению КПД и повреждению изоляции.
Использование правильных формул с учётом режима работы цепи и характеристик нагрузки позволяет повысить точность расчётов, продлить срок службы оборудования и обеспечить безопасность эксплуатации электрических установок.
Как рассчитать активную мощность в цепи переменного тока
Активная мощность обозначается как P и измеряется в ваттах (Вт). Она показывает, какая часть общей энергии в цепи реально преобразуется в полезную работу – например, в тепло, свет или движение. В цепи переменного тока активная мощность рассчитывается по формуле:
P = U × I × cos(φ)
Где:
U – действующее значение напряжения (в вольтах),
I – действующее значение тока (в амперах),
cos(φ) – коэффициент мощности, отражающий сдвиг фазы между током и напряжением.
Если нагрузка чисто активная (например, нагреватель), cos(φ) равен 1. В этом случае формула упрощается до P = U × I. При наличии реактивной составляющей (катушки или конденсаторы) значение cos(φ) будет меньше единицы, и активная мощность окажется ниже полной.
Для однофазной цепи переменного тока используйте указанную формулу напрямую. В трёхфазной системе при симметричной нагрузке применяется модифицированный вариант:
P = √3 × UЛ × IЛ × cos(φ)
Здесь UЛ и IЛ – линейное напряжение и ток соответственно. Этот подход позволяет точно учесть фазовый сдвиг и вычислить реальное потребление энергии в промышленной и бытовой электросети.
Для измерения коэффициента мощности используют приборы типа фазометра или ваттметра с функцией расчёта cos(φ). Если такой возможности нет, значение берётся из паспортных данных оборудования. Без точного учета этого параметра расчёт будет неточным, особенно в случае индуктивных нагрузок.
Важно также учитывать, что при постоянных значениях U и I изменение cos(φ) существенно влияет на итоговую мощность. Поэтому при проектировании электросети важно не только контролировать ток и напряжение, но и добиваться высокого коэффициента мощности за счёт компенсации реактивной энергии.
Расчёт полной мощности при известном напряжении и токе

Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА). Она характеризует общее количество энергии, передаваемой в цепи переменного тока, независимо от того, сколько из неё преобразуется в полезную работу.
Если известны значения действующего напряжения U (в вольтах) и тока I (в амперах), полная мощность рассчитывается по формуле:
S = U × I
Эта формула применима для как однофазных, так и трёхфазных цепей, но с определёнными особенностями:
- Для однофазной цепи формула остаётся в виде S = U × I, где U – линейное напряжение, I – ток в цепи.
- Для трёхфазной цепи применяется уточнённая формула: S = √3 × U × I, где U – линейное напряжение между фазами, I – ток в фазе.
Результат всегда выражается в вольт-амперах (ВА), даже если в цепи присутствует реактивная нагрузка. Это позволяет корректно учитывать все компоненты тока – активную и реактивную.
При использовании приборов для измерения тока и напряжения важно синхронизировать момент снятия показаний, особенно в переменных режимах, чтобы избежать искажений в расчётах. В автоматизированных системах такие значения обычно собираются с помощью трансформаторов тока и напряжения, подключённых к измерительным приборам или микроконтроллерам.
При расчёте в инженерной практике значения мощности часто выражаются в киловольт-амперах (кВА), где 1 кВА = 1000 ВА. Это удобно при работе с крупным оборудованием и системами распределения.
Определение реактивной мощности с использованием коэффициента мощности

Реактивная мощность обозначается буквой Q и измеряется в вольт-амперах реактивных (вар). Она не выполняет полезной работы, но необходима для создания электромагнитных полей в устройствах с индуктивной нагрузкой, таких как трансформаторы, двигатели и дроссели.
При известной полной мощности S и коэффициенте мощности cos φ реактивная мощность определяется по формуле:
Q = S × sin φ
Если отсутствует информация о полном угле сдвига фаз, но известен коэффициент мощности, можно воспользоваться выражением:
Q = P × tg φ, где P – активная мощность, tg φ = √(1 / cos² φ – 1)
Например, при активной мощности 10 кВт и коэффициенте мощности 0,8, сначала рассчитывается тангенс угла φ:
tg φ = √(1 / 0,8² – 1) ≈ 0,75
Затем реактивная мощность:
Q = 10 × 0,75 = 7,5 кВАр
Точное определение реактивной составляющей позволяет грамотно рассчитывать компенсацию с помощью батарей конденсаторов. Это снижает потери в сети и оптимизирует нагрузку на трансформаторы.
Формула расчёта мощности на резистивной нагрузке
Для резистивной нагрузки мощность рассчитывается по упрощённым формулам, поскольку ток и напряжение находятся в фазе, а коэффициент мощности равен единице.
Основные формулы:
- P = U × I – активная мощность, где U – напряжение в вольтах, I – ток в амперах.
- P = I² × R – если известен ток и сопротивление нагрузки.
- P = U² ÷ R – если известно только напряжение и сопротивление.
Рекомендации по применению:
- При измерении напряжения и тока на нагрузке обязательно учитывать, что данные должны быть RMS-значениями (действующими), особенно в цепях переменного тока.
- Если используется формула через сопротивление, убедитесь, что сопротивление не изменяется при нагреве, что актуально для нагревательных элементов.
- Для точных расчётов на переменном токе используйте формулы только в случае чисто активной нагрузки, например, лампы накаливания или ТЭНы без индуктивной составляющей.
В случае, если сопротивление неизвестно, его можно определить по формуле R = U ÷ I и затем использовать одну из вышеперечисленных формул для расчёта мощности.
Как найти мощность по сопротивлению и напряжению
Мощность на электрической нагрузке можно определить через известные величины сопротивления и напряжения с помощью формулы:
P = \frac{U^2}{R},
где P – мощность в ваттах (Вт), U – напряжение в вольтах (В), R – сопротивление в омах (Ω).
Формула вытекает из закона Ома и определения мощности: сила тока I связана с напряжением и сопротивлением как I = \frac{U}{R}. Подставляя это в формулу мощности P = U \times I, получаем искомое выражение.
Для точного расчёта важно использовать действующее (эффективное) значение переменного напряжения или постоянное напряжение, если речь о постоянном токе.
Пример: при напряжении 12 В и сопротивлении 4 Ω мощность будет P = \frac{12^2}{4} = \frac{144}{4} = 36 Вт.
Следует учитывать, что при расчётах для переменного тока напряжение и сопротивление должны соответствовать рабочим условиям цепи – учитывать наличие реактивных компонентов и характеристики нагрузки.
Для однофазной сети активная мощность рассчитывается по формуле: P = U × I × cos φ, где U – напряжение в вольтах, I – ток в амперах, cos φ – коэффициент мощности. Эта формула учитывает только активную мощность, фактически потребляемую нагрузкой.
Полная мощность в однофазной цепи определяется как S = U × I (в вольт-амперах), а реактивная мощность вычисляется через Q = U × I × sin φ. Для точного расчёта необходимо знать угол сдвига фаз между током и напряжением.
В трёхфазной сети мощность рассчитывается иначе в зависимости от типа подключения. При звездообразном соединении фазная мощность выражается формулой P = √3 × UL × IФ × cos φ, где UL – линейное напряжение, IФ – фазный ток. Учитывая, что фазное напряжение в звезде равняется UФ = UL / √3, формула позволяет быстро вычислить мощность по известным параметрам.
При треугольном соединении мощность также определяется формулой P = √3 × UL × IЛ × cos φ, где IЛ – линейный ток. В данном случае ток нагрузки равен фазному току, а напряжение – линейному.
Для трёхфазных систем важен правильный учёт коэффициента мощности и баланса фаз. Несбалансированная нагрузка приводит к появлению нулевого тока и искажает результаты измерений. Рекомендуется использовать измерительные приборы, позволяющие фиксировать фазные параметры отдельно.
Для практического расчёта активной мощности в трёхфазных сетях наиболее распространена формула P = √3 × U × I × cos φ, где все параметры измеряются между линиями и по линии соответственно. Это упрощает контроль и позволяет быстро оценить нагрузку.
Учет косинуса фи при расчете мощности на нагрузке

Косинус фи (cos φ) отражает угол сдвига фаз между напряжением и током в цепи переменного тока. Этот параметр необходим для точного определения активной мощности нагрузки, поскольку общая мощность (полная мощность) включает как активную, так и реактивную составляющие.
Формула для расчета активной мощности P, учитывающей косинус фи:
P = U × I × cos φ,
где U – напряжение в вольтах (В), I – ток в амперах (А), cos φ – коэффициент мощности, безразмерная величина от 0 до 1.
Значение cos φ показывает долю полной мощности, которая преобразуется в полезную работу (тепло, механическую энергию и т.д.). При cos φ = 1 нагрузка является чисто активной (резистивной), при cos φ < 1 – присутствует реактивная составляющая, которая создает дополнительную нагрузку на сеть без полезной работы.
Для трехфазной нагрузки активная мощность рассчитывается по формуле:
P = √3 × U × I × cos φ,
где U – линейное напряжение.
При проектировании и анализе электрических цепей важно измерять и учитывать cos φ, чтобы избежать излишних потерь и оптимизировать энергопотребление. Для повышения cos φ используют устройства компенсации реактивной мощности (конденсаторы, синхронные компенсаторы).
Точное определение cos φ позволяет корректно рассчитывать нагрузку по мощности, выбирать оборудование и обеспечивать стабильную работу электросети без перегрузок и снижения качества электроэнергии.
| Параметр | Обозначение | Единица измерения |
|---|---|---|
| Напряжение | U | Вольт (В) |
| Ток | I | Ампер (А) |
| Косинус фи | cos φ | Безразмерный |
| Активная мощность | P | Вт (Ватт) |
Применение формул расчета мощности в бытовых и промышленных условиях
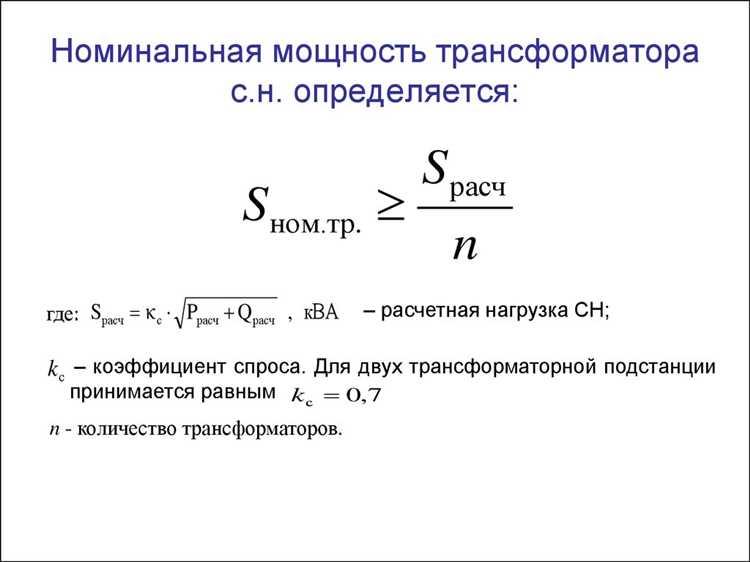
В бытовых условиях расчёт мощности электрической нагрузки помогает определить максимальную допустимую нагрузку на проводку и электрооборудование. Для этого применяют формулу активной мощности P = U × I × cos φ, где U – напряжение, I – ток, cos φ – коэффициент мощности. Точное вычисление позволяет избежать перегрева кабелей и выхода из строя бытовых приборов.
В промышленности важен учёт полной мощности S = U × I × √3 для трёхфазных сетей, а также разделение на активную и реактивную мощность для оптимизации работы электросистем. Формулы применяются для расчёта нагрузки трансформаторов, электродвигателей и распределительных щитов. Контроль коэффициента мощности снижает потери энергии и уменьшает штрафы от энергоснабжающих компаний.
Расчёты мощности в промышленности часто используют при проектировании систем автоматизации и выбора оборудования с учётом номинальных параметров. Формулы помогают оценить нагрузку в аварийных режимах и при пуске электродвигателей, что обеспечивает безопасность и надёжность эксплуатации.
Для бытовых приборов важна точность расчёта мощности при подключении нескольких устройств к одной линии, чтобы предотвратить срабатывание защитных устройств и обеспечить стабильное питание. Использование формул позволяет подобрать автоматические выключатели по номинальному току и подобрать оптимальные сечения проводов.
В промышленном масштабе расчёты помогают планировать энергопотребление, обеспечивать баланс нагрузки на сети и оптимизировать расходы на электроэнергию. Применение формул позволяет избежать избыточных затрат на оборудование и снизить эксплуатационные расходы.
Вопрос-ответ:
Как определить мощность на резистивной нагрузке с помощью напряжения и сопротивления?
Для расчёта мощности на резистивной нагрузке применяют формулу P = U² / R, где P — мощность в ваттах, U — напряжение в вольтах, а R — сопротивление в омах. Эта формула выводится из закона Ома и позволяет вычислить мощность, выделяемую на резисторе, используя измеренное напряжение и известное сопротивление.
Чем отличается активная мощность от полной в цепи переменного тока?
Активная мощность — это часть мощности, которая преобразуется в полезную работу или тепло, и измеряется в ваттах (Вт). Полная мощность учитывает не только активную, но и реактивную составляющую, отражающую энергию, которая периодически возвращается в источник и измеряется в вольт-амперах (ВА). Реактивная мощность возникает из-за наличия индуктивных или емкостных элементов в цепи и не выполняет полезную работу.
Как учитывать коэффициент мощности при расчёте мощности на нагрузке?
Коэффициент мощности (cos φ) отражает соотношение между активной и полной мощностью в цепи переменного тока. Для расчёта активной мощности P используется формула P = S × cos φ, где S — полная мощность. Если известна мощность нагрузки и cos φ, то можно определить реальную нагрузку, учитывая влияние реактивных элементов, которые изменяют фазовый угол между током и напряжением.
Какие формулы применимы для расчёта мощности в трёхфазной электрической сети?
В трёхфазной системе мощность рассчитывается по формуле P = √3 × U × I × cos φ, где U — линейное напряжение, I — линейный ток, а cos φ — коэффициент мощности. Эта формула учитывает взаимное смещение фаз и используется для определения активной мощности в трёхфазных цепях с симметричной нагрузкой.
Как рассчитать мощность на резистивно-индуктивной нагрузке с учетом фазового сдвига?
При наличии индуктивной нагрузки ток и напряжение смещены по фазе. Для определения активной мощности P необходимо учитывать коэффициент мощности cos φ, связанный с фазовым углом сдвига. Формула выглядит так: P = U × I × cos φ. Здесь U — напряжение, I — ток, а cos φ показывает долю мощности, реально расходуемой нагрузкой, с учётом сдвига фаз.
Какая формула используется для расчёта мощности на резистивной нагрузке?
Для резистивной нагрузки мощность вычисляется по формуле P = U × I, где P — мощность в ваттах, U — напряжение в вольтах, а I — сила тока в амперах. Также можно использовать выражение P = I² × R или P = U² / R, где R — сопротивление нагрузки. Эти формулы подходят для участков цепи, где нагрузка полностью активная, без реактивных компонентов.






