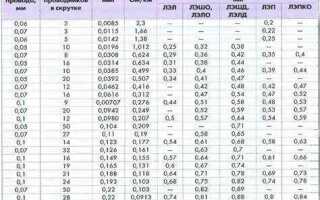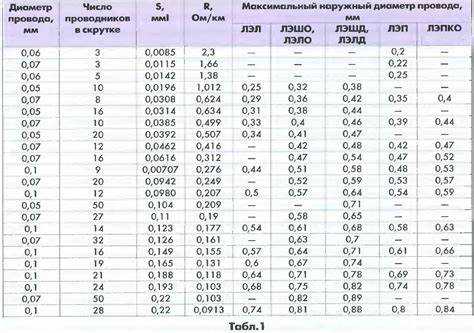
В технических расчетах часто возникают путаница и ошибки при подмене понятий «сечение» и «диаметр». Хотя оба параметра связаны с геометрическими характеристиками тел вращения и труб, они выполняют принципиально разные функции в инженерной практике. Диаметр определяет линейный размер круга или цилиндра, тогда как сечение относится к площади поперечного среза объекта и играет ключевую роль в расчете нагрузок, сопротивления материала и пропускной способности.
Для сплошного круглого стержня площадь поперечного сечения S рассчитывается по формуле: S = πd² / 4, где d – диаметр. В случае полых труб используется выражение: S = π(D² – d²) / 4, где D – внешний, d – внутренний диаметр. Эти различия критичны при определении прочностных характеристик, особенно при расчетах на сжатие, изгиб или кручение.
В гидравлике и пневматике выбор между использованием диаметра или сечения зависит от задачи. Например, расчет расхода жидкости осуществляется через площадь проходного сечения, а не через диаметр. Ошибки в интерпретации могут привести к некорректному подбору трубопроводов, фитингов и насосного оборудования.
При проектировании металлических конструкций, расчетах армирования или подборе кабельной продукции сечение определяет рабочие характеристики элемента. В то время как диаметр может быть удобен при визуальной оценке или подборе соединительных элементов, для прочностных расчетов оперируют исключительно площадью поперечного сечения.
Как рассчитать площадь сечения круглого элемента по диаметру

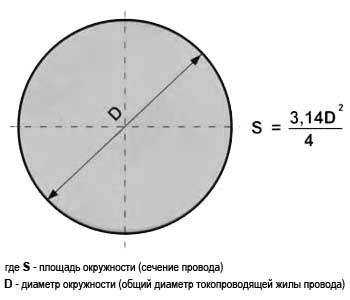
Площадь поперечного сечения круглого элемента рассчитывается по формуле: S = π × (d² / 4), где S – искомая площадь в квадратных миллиметрах или сантиметрах, d – диаметр элемента в тех же единицах, π ≈ 3,1416.
Для получения точного значения важно использовать диаметр в виде числа с десятичными знаками, если он измерен с высокой точностью. Например, если диаметр стального прута составляет 12,7 мм, то площадь его поперечного сечения будет равна: S = 3,1416 × (12,7² / 4) ≈ 126,68 мм².
Если задан не диаметр, а радиус, его необходимо удвоить для подстановки в формулу. Пренебрежение точным значением диаметра приводит к искажению расчетов, особенно при подборе сечений под допустимые нагрузки.
При инженерных расчетах рекомендуется указывать единицы измерения рядом с результатом. Например, «S = 126,68 мм²» – это важно для предотвращения ошибок при переводе данных в другие системы или при передаче на производство.
Также следует учитывать, что округление значения диаметра даже на 0,1 мм влечёт изменение площади сечения на несколько процентов, что может оказаться критичным при расчете несущей способности конструкции.
Влияние диаметра и сечения на прочностные характеристики материала
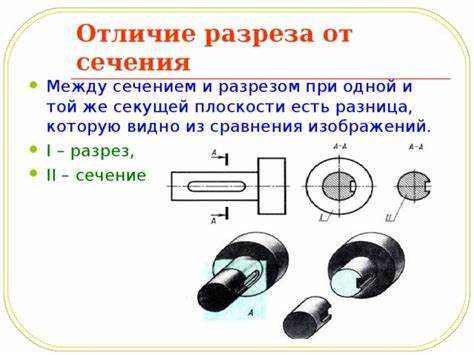
Прочностные характеристики материала напрямую зависят от геометрических параметров, таких как диаметр и площадь поперечного сечения. Эти параметры определяют устойчивость элемента к нагрузкам на растяжение, сжатие и изгиб.
При растяжении или сжатии прочность определяется по формуле:
σ = F / A,
где σ – напряжение, F – приложенная сила, A – площадь поперечного сечения. Чем больше сечение, тем меньшие напряжения возникают при той же нагрузке. Это критично при проектировании несущих конструкций и валов, передающих крутящий момент.
Для круглых элементов площадь сечения рассчитывается как:
A = π × (d² / 4),
где d – диаметр. Таким образом, увеличение диаметра даже на незначительное значение приводит к значительному увеличению площади и, следовательно, повышению несущей способности.
- Удвоение диаметра увеличивает площадь сечения в 4 раза, а это в 4 раза снижает удельное напряжение при одинаковой нагрузке.
- При изгибе момент инерции круглого сечения определяется как I = π × d⁴ / 64. Он возрастает в четвёртой степени от диаметра, что особенно важно для элементов, подверженных изгибу или кручению.
При подборе диаметра и сечения необходимо учитывать не только расчетные нагрузки, но и тип материала:
- Сталь требует меньшего сечения по сравнению с алюминием или пластиком для одинаковых нагрузок.
- Для хрупких материалов критично избегать концентрации напряжений – малые диаметры и острые переходы повышают риск разрушения.
Оптимизация диаметра и сечения позволяет сократить массу конструкции без потери прочности. Это особенно важно в машиностроении и авиации, где вес является критическим параметром.
Когда в расчетах использовать диаметр, а когда – площадь сечения
Площадь сечения применяется в расчетах, где требуется определить силовую нагрузку, распределенную по поперечному сечению. Это критично при вычислении нормальных напряжений по формуле σ = F/A, где F – осевая сила, A – площадь сечения. Без учета площади невозможно провести корректный расчет на растяжение, сжатие, сдвиг или устойчивость элемента. Площадь сечения также используется при подборе арматуры, расчете деформаций и проверке несущей способности элементов.
Если известно только значение диаметра круглого сечения, площадь можно вычислить по формуле A = π·d²/4. Это необходимо, когда исходные данные заданы через диаметр, но расчет требует площади. Противоположная ситуация возникает при работе с конечными элементами, когда сечение уже известно, а диаметр нужен только для сопоставления геометрии.
Таким образом, диаметр удобен для геометрических и технологических задач, тогда как площадь сечения – ключевой параметр для механических расчетов прочности, устойчивости и жесткости. Подход к выбору параметра всегда должен соответствовать характеру задачи и типу действующих нагрузок.
Преобразование диаметра в сечение при проектировании
При проектировании элементов круглого сечения расчет площади поперечного сечения на основе диаметра выполняется по формуле: S = π × (d² / 4), где S – площадь в мм² или м², d – диаметр в тех же единицах. Этот расчет обязателен при определении несущей способности, сопротивления изгибу или расчетах теплопередачи.
Например, если задан диаметр круглой стальной балки 40 мм, площадь сечения будет: π × (40² / 4) = π × 400 = 1256,64 мм². Эта величина используется в расчетах напряжений по формуле: σ = F / S, где F – приложенная сила.
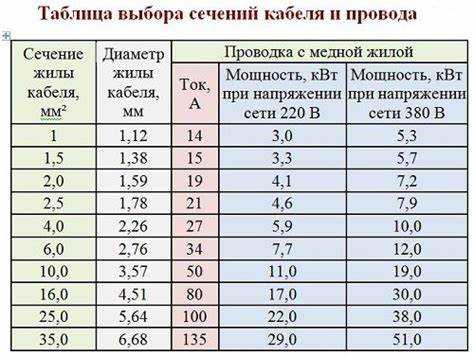
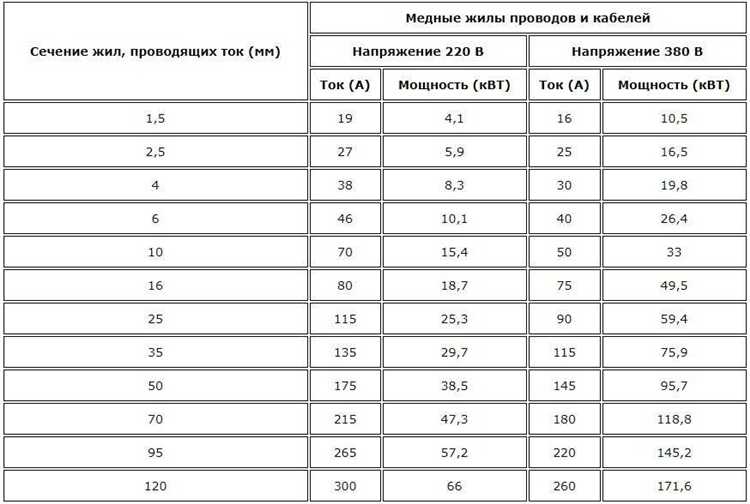
При расчете проводников и трубопроводов также используется площадь, а не диаметр напрямую. Для медного кабеля, рассчитанного на токовую нагрузку, переход от диаметра жилы к сечению необходим для подбора допустимой плотности тока. Ошибка в переводе может привести к перегреву и выходу из строя.
В инженерной практике важно сохранять точность: округление площади недопустимо, если элемент работает на предельных нагрузках. Следует использовать диаметр с точностью до десятых миллиметра и применять константу π не менее чем до четырёх знаков (3,1416).
Переход от диаметра к площади нужен не только в статике. В гидродинамике через площадь рассчитывается скорость потока: v = Q / S, где Q – объемный расход. От правильного пересчета зависит точность всей системы управления жидкостями или газами.
Ошибки при подмене понятий сечения и диаметра в инженерных чертежах
В инженерных чертежах подмена диаметра площадью поперечного сечения приводит к критическим просчётам. Наиболее распространённая ошибка – использование обозначения Ø (диаметр) вместо указания реальной площади сечения, особенно при расчётах на прочность, прогиб или гидравлическое сопротивление.
Если в расчётах нагрузки на вал указывается только диаметр без уточнения геометрии сечения, это может привести к недооценке допустимого крутящего момента. Например, полый вал и сплошной с тем же внешним диаметром имеют принципиально разные характеристики, так как момент инерции и модуль сечения существенно различаются.
В чертежах труб и профилей часто пренебрегают толщиной стенки, указывая только внешний диаметр. В результате проектировщик использует некорректную площадь при тепловых или механических расчётах. При вычислении теплопередачи или напряжений в таких случаях необходимо использовать реальное внутреннее сечение, а не внешние габариты.
Ошибка также возникает при передаче чертежей между подразделениями. Если на схеме проставлен только диаметр, а инженер-расчётчик принимает его за сечение, расчёт давления, потерь на трение или устойчивости конструкции будет искажен. Особенно это критично в гидравлике и аэродинамике, где сечение определяет скорость потока и энергию.
Чтобы исключить подобные ошибки, необходимо придерживаться строгой маркировки: использовать Ø только для обозначения диаметра и обязательно указывать, является ли он внутренним, внешним или номинальным. При ссылке на сечение предпочтительно прямо указывать его площадь в мм² с пояснением, как она получена – например, для кольцевого профиля: \( S = \pi (D^2 — d^2)/4 \).
Рекомендуется сопровождать каждый размер пояснительной надписью, особенно в случаях, когда конструкция содержит сложные геометрические переходы. Это исключает недопонимание между конструктором, технологом и инженером-расчётчиком.
Примеры применения сечения и диаметра в расчетах нагрузок и давления
При расчёте внутреннего давления в трубопроводах применяется наружный или внутренний диаметр в зависимости от метода. Например, для расчёта кольцевого напряжения по формуле Ламе учитывается внутренний диаметр трубы и толщина стенки. Ошибка в подстановке наружного диаметра вместо внутреннего может привести к недопустимому занижению результата и разрушению конструкции под давлением.
В гидравлических расчётах, например, при определении скорости потока жидкости по уравнению расхода \( Q = v \cdot A \), используется именно площадь поперечного сечения A, которая рассчитывается по формуле \( A = \frac{\pi d^2}{4} \). Подстановка диаметра напрямую в уравнение без преобразования к площади делает расчёт некорректным. Это критично при проектировании насосных систем, где отклонение даже на 5–10% может вызвать кавитацию или потерю давления в узлах.
В строительной механике при расчёте растянутых или сжатых элементов, таких как стальные стержни, используется площадь поперечного сечения для определения нормального напряжения: \( \sigma = \frac{F}{A} \). Подстановка диаметра вместо площади приводит к систематической ошибке. Например, при диаметре 20 мм площадь будет \( A = 314 \text{ мм}^2 \), тогда как ошибочная подстановка 20 вместо площади даёт завышенное напряжение в 15,7 раза.
При расчётах давления в гидроцилиндрах или пневматических системах сила определяется как \( F = P \cdot A \), где A – это площадь поперечного сечения поршня. Использование диаметра без пересчёта в площадь искажают значение силы в несколько раз. Особенно важно это при подборе клапанов, приводов и управляющих устройств.
В аэродинамике и расчётах сопротивления тел, движущихся в газах и жидкостях, площадь сечения играет ключевую роль в определении лобового сопротивления. Диаметр в таких случаях может использоваться только как вспомогательная величина, например, для вычисления \( A = \frac{\pi d^2}{4} \), но не как самостоятельная переменная в уравнении сопротивления.