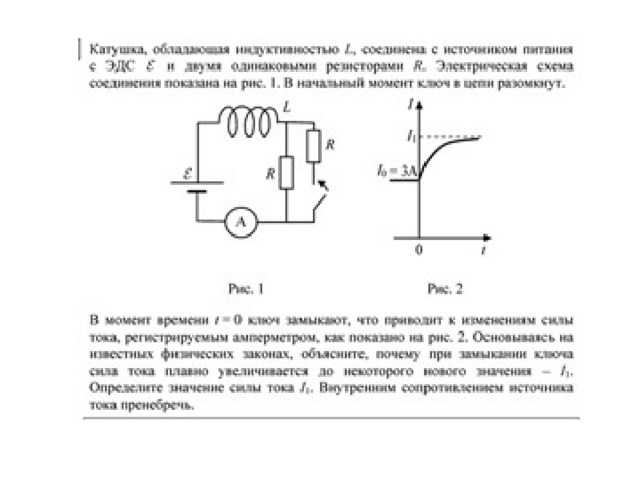
Самоиндукция – это процесс, при котором в проводнике возникает электродвижущая сила (ЭДС) в ответ на изменение собственного тока. В отличие от взаимной индукции, где ЭДС возникает во втором контуре, самоиндукция касается исключительно одного проводящего контура. Явление обусловлено тем, что любой изменяющийся ток порождает переменное магнитное поле, которое, в свою очередь, индуцирует ЭДС, противодействующую изменению тока.
Численно эффект самоиндукции описывается с помощью индуктивности L, измеряемой в генри (Гн). Индуктивность зависит от геометрии проводника, его длины, сечения, числа витков в катушке и магнитной проницаемости среды. Например, катушка с ферромагнитным сердечником имеет существенно большую индуктивность по сравнению с воздушной катушкой при равных размерах.
Формула ЭДС самоиндукции записывается как ε = -L(dI/dt), где ε – индуцированная ЭДС, L – индуктивность, dI/dt – скорость изменения тока. Знак минус отражает правило Ленца: индуцированная ЭДС всегда направлена против причины её возникновения. Это приводит к замедлению нарастания или спадания тока в цепях с катушками, что критично для проектирования трансформаторов, фильтров, импульсных источников питания и дросселей.
При практическом расчёте следует учитывать паразитную индуктивность в печатных платах и соединительных проводниках, так как она может вызывать нежелательные переходные процессы, особенно в высокочастотной электронике. Для минимизации эффекта рекомендуется использовать проводники с минимальной петлей тока и катушки с экранировкой. В микросхемах с высокой плотностью интеграции применяются специальные архитектуры с подавлением самоиндуктивных выбросов.
Как изменение силы тока в катушке вызывает ЭДС самоиндукции
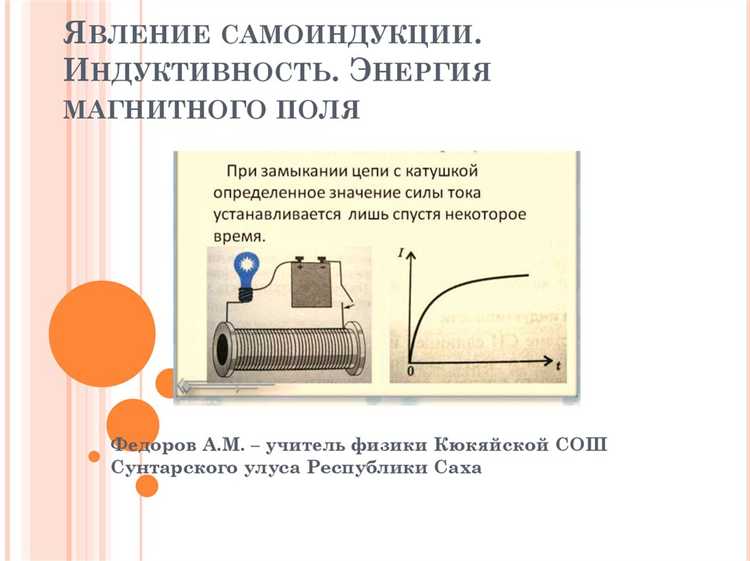
При изменении силы тока в замкнутой катушке происходит изменение магнитного потока через её витки. Согласно закону Фарадея, это изменение вызывает возникновение электродвижущей силы индукции. В случае замкнутой катушки без внешнего магнитного поля речь идёт о самоиндукции.
Если ток в катушке возрастает, увеличивается создаваемое ею магнитное поле, что приводит к росту магнитного потока. В ответ возникает индукционная ЭДС, направленная против увеличения тока – это проявление закона Ленца. При уменьшении тока магнитный поток убывает, и индуцируемая ЭДС стремится сохранить ток, возникая в том же направлении, что и убывающий ток.
Величина ЭДС самоиндукции определяется выражением: ε = -L (dI/dt), где L – индуктивность катушки, dI/dt – скорость изменения силы тока. Индуктивность зависит от геометрии катушки (число витков, длина, площадь поперечного сечения) и магнитной проницаемости сердечника.
Для минимизации ЭДС самоиндукции в чувствительных цепях рекомендуют использовать катушки с малым числом витков и без ферромагнитного сердечника. В импульсных схемах применяют диоды защиты от самоиндукции, шунтирующие ток при резком обрыве цепи, предотвращая повреждение компонентов скачком напряжения.
ЭДС самоиндукции – ключевое явление в трансформаторах, дросселях, индуктивных датчиках. Правильный учёт этого эффекта необходим при расчётах переходных процессов и выборе элементной базы в электротехнических системах.
Почему в цепях с индуктивностью возникает задержка нарастания тока
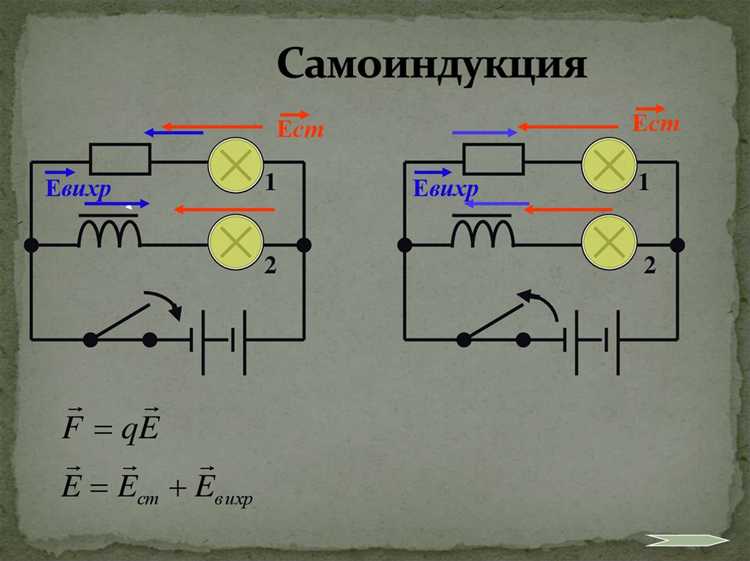
Когда в цепь с катушкой индуктивности подаётся напряжение, ток не достигает максимального значения мгновенно из-за противодействия, создаваемого ЭДС самоиндукции. Эта электродвижущая сила направлена противоположно изменению тока, вызывающему её появление, согласно закону Ленца.
Математически это описывается уравнением: \( V = L \frac{dI}{dt} + IR \), где \( V \) – приложенное напряжение, \( L \) – индуктивность, \( I \) – ток, \( R \) – сопротивление цепи. В момент включения тока \( I = 0 \), и вся энергия уходит на преодоление ЭДС самоиндукции, ограничивая скорость изменения тока \( \frac{dI}{dt} \).
Характерное время реакции цепи определяется постоянной времени \( \tau = \frac{L}{R} \). За время, равное одной \( \tau \), ток достигает примерно 63% от установившегося значения. При больших значениях \( L \) или малых \( R \) индуктивный эффект становится особенно заметным – ток нарастает медленно, что критично при проектировании импульсных источников питания и фильтров.
Для уменьшения задержки используют методы снижения индуктивности: минимизация количества витков катушки, применение магнитопроводов с низкой проницаемостью, а также корректный выбор конструкции и топологии проводников. В высокочастотных схемах дополнительно применяются ферритовые элементы для контроля и компенсации паразитной индуктивности.
Игнорирование эффекта задержки может привести к нарушению синхронизации и перегреву компонентов из-за неконтролируемых переходных процессов. Поэтому при моделировании цепей с индуктивными элементами обязательным является учёт дифференциальных характеристик на этапе анализа переходных процессов.
Как рассчитать ЭДС самоиндукции по закону Ленца и Фарадея
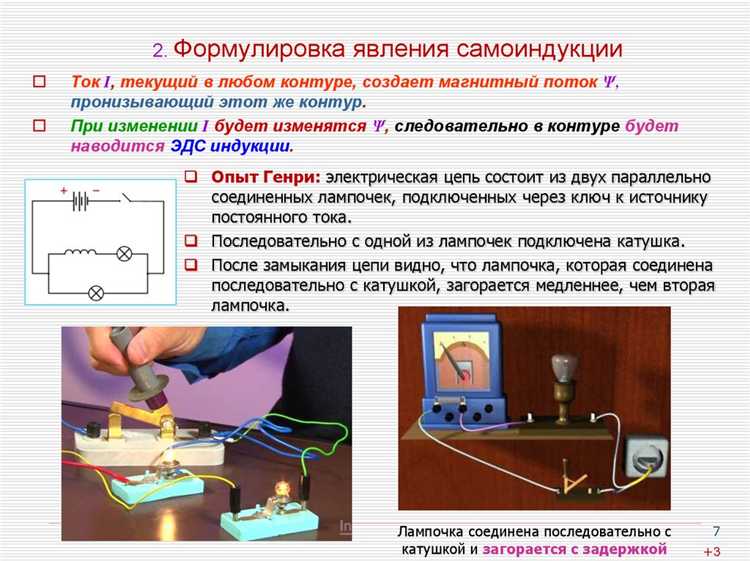
ЭДС самоиндукции возникает в проводнике при изменении тока, проходящего через него. Для её расчёта используется закон электромагнитной индукции Фарадея, с учётом направления по закону Ленца:
Формула:
𝓔 = -L · (dI/dt)
- 𝓔 – электродвижущая сила самоиндукции (в вольтах, В)
- L – индуктивность контура (в генри, Гн)
- dI/dt – скорость изменения тока во времени (А/с)
Знак минус в формуле отражает направление индукционного тока, противодействующее причине его возникновения, в соответствии с законом Ленца.
Для расчёта необходимы:
- Измерить или задать индуктивность катушки (например, с помощью прибора или расчётом по геометрии и числу витков).
- Определить, как быстро изменяется ток: найти производную силы тока по времени или рассчитать ΔI / Δt при линейном изменении.
- Подставить значения в формулу и учесть знак для определения направления ЭДС.
Пример: при L = 0.5 Гн, ток изменяется от 0 до 2 А за 0.01 с:
dI/dt = (2 — 0) / 0.01 = 200 А/с
𝓔 = -0.5 × 200 = -100 В
Полученное значение указывает, что индукционная ЭДС направлена против изменения тока.
Роль самоиндукции в работе реле и электромагнитов
Самоиндукция оказывает непосредственное влияние на характеристики коммутационных процессов в реле и электромагнитах. При размыкании цепи, содержащей катушку с током, возникает ЭДС самоиндукции, направленная против изменения тока. Эта ЭДС может достигать десятков или даже сотен вольт в зависимости от скорости изменения тока и индуктивности обмотки.
В реле это приводит к появлению высоковольтных импульсов, которые способны вызвать пробой изоляции, деградацию контактов и помехи в цепях управления. Для минимизации этих эффектов рекомендуется применять демпфирующие цепи: диоды Шоттки (в постоянных цепях), варисторы или RC-цепочки (в переменных). Установка обратного диода параллельно обмотке реле позволяет погасить ЭДС самоиндукции, преобразовав её в тепловую энергию.
В электромагнитах самоиндукция определяет скорость нарастания и спадания магнитного поля. При подаче напряжения ток в катушке возрастает не мгновенно, а по экспоненциальному закону, что задерживает развитие магнитного потока. Это критично в системах, где требуется быстрый отклик – например, в исполнительных механизмах автоматизированных устройств. Уменьшение времени срабатывания достигается снижением индуктивности обмотки или увеличением напряжения питания при кратковременной подаче.
Самоиндукция также способствует возникновению механических колебаний якоря, если отключение происходит без подавления ЭДС. Это снижает точность и ресурс устройства. Для исключения вибрации необходимо обеспечить быстрое гашение остаточного магнитного поля, что достигается применением ферромагнитных сердечников с высоким коэффициентом демагнетизации или активным управлением током через драйверы.
Понимание и контроль самоиндукции – ключевой фактор при проектировании надежных и долговечных реле и электромагнитных систем.
Как снизить влияние самоиндукции в электрических схемах

Для уменьшения эффекта самоиндукции в цепях постоянного и переменного тока применяются проверенные технические приёмы. Один из наиболее эффективных – использование шунтирующих диодов в цепях с индуктивной нагрузкой. Диод, подключённый параллельно катушке индуктивности в обратной полярности, ограничивает выброс напряжения при размыкании цепи, предотвращая повреждение компонентов.
При проектировании печатных плат важно минимизировать длину проводников, по которым протекает импульсный ток через индуктивные элементы. Длинные дорожки увеличивают паразитную индуктивность, способствуя появлению высокочастотных помех. Применение многослойных плат с плотной укладкой слоёв питания и земли дополнительно снижает помехи за счёт уменьшения замкнутой площади токов.
В цепях питания импульсных устройств рекомендуется устанавливать снабберные RC-цепочки, подключённые параллельно переключающим элементам. Они эффективно гасят перенапряжения, вызванные резким изменением тока через индуктивность. Параметры RC-снаббера подбираются экспериментально, исходя из характеристик нагрузки и коммутирующего транзистора.
Ещё один способ снижения самоиндукции – использование дросселей с ферритовым сердечником, имеющим высокую магнитную проницаемость. Такие сердечники позволяют уменьшить число витков и, следовательно, снизить индуктивность при сохранении необходимого сопротивления переменному току.
Для силовых схем целесообразно применять мягкое (двухступенчатое) выключение индуктивной нагрузки. Постепенное снижение тока снижает темп изменения магнитного потока и, как следствие, напряжение самоиндукции. Это реализуется, например, с помощью широтно-импульсной модуляции с понижающим коэффициентом заполнения на завершающей стадии коммутации.
Применение самоиндукции в импульсных источниках питания

Самоиндукция в импульсных источниках питания реализуется через катушки индуктивности, обеспечивающие стабилизацию тока и формирование заданных импульсов напряжения. Основная задача – минимизировать скачки тока при переключении ключевых элементов и снизить потери энергии.
Ключевые аспекты использования самоиндукции в таких системах:
- Формирование фронтов напряжения и ограничения пиков тока при включении и выключении транзисторов;
- Накопление и последующая отдача энергии, обеспечивающая повышение КПД устройства;
- Фильтрация высокочастотных помех, возникающих при быстром переключении;
- Снижение электромагнитных излучений за счет плавного изменения тока.
Практические рекомендации по выбору индуктивности:
- Расчет индуктивности производится с учетом требуемого времени нарастания тока и максимального допустимого пульсационного тока.
- Использовать ферритовые сердечники с высокой магнитной проницаемостью для уменьшения габаритов и повышения эффективности.
- Обеспечить допустимый ток насыщения сердечника, превышающий максимальный рабочий ток не менее чем на 20% для предотвращения потери индуктивности.
- Минимизировать сопротивление обмотки для снижения тепловых потерь и повышения стабильности параметров.
Типовые схемы импульсных источников питания – преобразователи типа buck, boost, buck-boost – требуют точного согласования индуктивности с частотой переключения и емкостью конденсаторов для достижения оптимального режима работы.
Без контроля параметров самоиндукции возможно возникновение перенапряжений, приводящих к повреждению ключевых компонентов и снижению надежности. Следовательно, грамотный выбор и расчет индуктивных элементов критичен для долговременной стабильности и эффективности ИИП.
Вопрос-ответ:
Что такое самоиндукция и как она связана с электромагнитной индукцией?
Самоиндукция — это процесс возникновения электродвижущей силы в проводнике из-за изменения тока, проходящего по нему. Это частный случай явления электромагнитной индукции, при котором изменение магнитного потока происходит внутри самого проводника, а не извне. Таким образом, самоиндукция — это реакция проводника на собственное изменение тока, приводящая к появлению противодействующего напряжения.
Почему в цепях с самоиндукцией возникает противоэлектродвижущая сила?
Противоэлектродвижущая сила возникает из-за того, что изменение тока в проводнике вызывает изменение магнитного поля вокруг него. Это изменение поля индуцирует напряжение, направленное так, чтобы препятствовать изменению тока. Такая реакция связана с законом Ленца, который указывает, что индуцированное напряжение всегда направлено против причины его возникновения, то есть против изменения тока.
Какие факторы влияют на величину коэффициента самоиндукции?
Коэффициент самоиндукции зависит от нескольких параметров: геометрии проводника (например, длины и формы катушки), количества витков в катушке, магнитной проницаемости среды вокруг проводника, а также от площади поперечного сечения катушки. Чем больше витков и чем выше магнитная проницаемость, тем выше коэффициент самоиндукции. Это связано с тем, что магнитное поле, создаваемое током, становится сильнее и изменяется интенсивнее.
Как проявляется эффект самоиндукции в цепях с переменным током?
При переменном токе сила тока непрерывно меняется, а значит, магнитное поле вокруг проводника тоже постоянно изменяется. Из-за этого в проводнике возникает напряжение самоиндукции, которое сдерживает изменения тока. Вследствие этого ток в цепи запаздывает по фазе относительно напряжения, что влияет на параметры цепи, например, вызывает появление индуктивного сопротивления. Это явление важно учитывать при проектировании электрических устройств.
Можно ли наблюдать самоиндукцию в обычных проводах или только в катушках?
Самоиндукция возможна в любом проводнике, по которому течёт переменный ток, так как любое изменение тока вызывает изменение магнитного поля и, соответственно, возникновение индуцированного напряжения. Однако в катушках самоиндукция проявляется намного сильнее из-за большого числа витков и концентрированного магнитного поля. В простых прямых проводах эффект очень слабый и обычно не влияет на работу цепи.






