Как найти силу тока в каждом проводнике

Определение силы тока в каждом элементе электрической цепи требует учёта конкретной схемы соединения: последовательной, параллельной или смешанной. Для последовательного соединения сила тока одинакова во всех участках цепи и вычисляется по закону Ома: I = U / R, где U – общее напряжение, R – суммарное сопротивление.

При параллельном соединении общий ток распределяется между ветвями обратно пропорционально их сопротивлениям. Формула для силы тока в конкретном проводнике: I_n = U / R_n, где R_n – сопротивление данного участка. Напряжение во всех ветвях одинаково, что упрощает расчёты при наличии нескольких параллельных ветвей.

В случае смешанных схем необходим поэтапный подход: сначала рассчитываются эквивалентные сопротивления участков, затем – токи в узлах с помощью правил Кирхгофа. Используется первое правило (сумма токов в узле равна нулю) и второе правило (сумма падений напряжений по замкнутому контуру равна суммарному ЭДС).

Для практического применения важно точно измерить сопротивления каждого проводника и напряжение источника. Расчёт токов в сложной цепи можно автоматизировать с помощью методов узлового анализа или методом контурных токов, особенно при наличии нескольких источников ЭДС и сопротивлений с различными значениями.

Как определить эквивалентное сопротивление сложной цепи

Для расчёта эквивалентного сопротивления сложной цепи необходимо поэтапно упрощать конфигурацию, заменяя участки с параллельным и последовательным соединением эквивалентными элементами. При последовательном соединении сопротивлений используется сумма: \( R_{\text{экв}} = R_1 + R_2 + \dots + R_n \). При параллельном – применяется формула: \( \frac{1}{R_{\text{экв}}} = \frac{1}{R_1} + \frac{1}{R_2} + \dots + \frac{1}{R_n} \).

Если соединения комбинированные, необходимо начинать с тех участков, где конфигурация однозначно определена – например, два резистора, подключённые к одной точке с обеих сторон. После расчёта эквивалентного сопротивления участка, он заменяется одним резистором, и схема пересматривается на предмет следующих однозначных соединений.

Особое внимание следует уделять узлам: при параллельном соединении важно убедиться, что начало и конец каждого элемента подключены к одним и тем же двум точкам. В противном случае соединение не является параллельным. Визуализация схемы помогает избежать ошибок: рекомендуется перерисовывать упрощённые участки после каждой итерации.

В случаях, когда схема не сводится к простой последовательности преобразований, применяется метод преобразования «треугольник–звезда» и обратно. Это позволяет сократить количество элементов между узлами и продолжить упрощение цепи до вычислимой структуры.

После полного упрощения схема должна свестись к одному эквивалентному резистору между двумя точками питания. Его значение и есть искомое эквивалентное сопротивление цепи.

Расчёт силы тока в резисторе при последовательном соединении

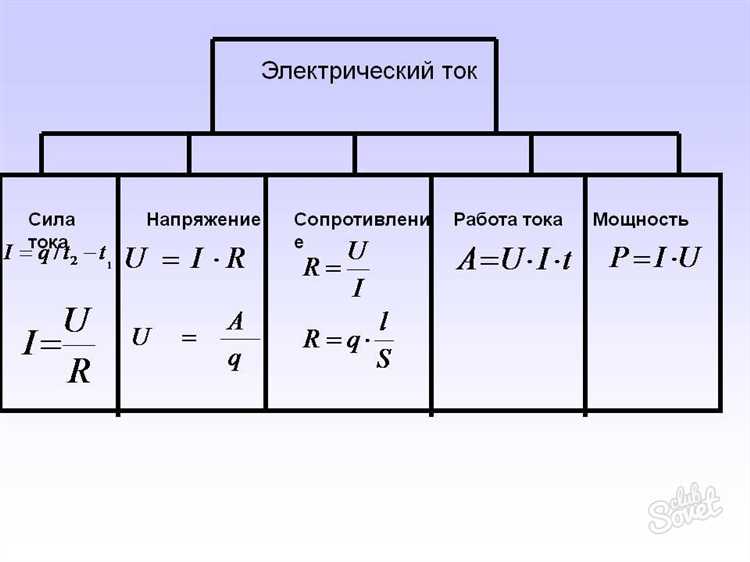
При последовательном соединении резисторов сила тока во всех участках цепи одинакова. Для расчёта тока в любом резисторе используется закон Ома: I = U / R, где I – сила тока (в амперах), U – общее напряжение источника (в вольтах), R – суммарное сопротивление цепи (в омах).

Сначала рассчитывается эквивалентное сопротивление всей цепи:

R_экв = R₁ + R₂ + … + R_n

Затем определяется сила тока:

I = U / R_экв

Например, если три резистора с сопротивлениями 5 Ом, 10 Ом и 15 Ом соединены последовательно и к ним приложено напряжение 12 В, расчёты будут следующими:

Сила тока в каждом резисторе будет равна 0,4 А независимо от номинала сопротивления. Распределение напряжения по каждому элементу зависит от его сопротивления, но ток везде одинаков.

Для точного измерения рекомендуется использовать цифровой мультиметр, подключённый последовательно с одним из резисторов. Важно учитывать, что обрыв любого элемента разрывает всю цепь и приводит к нулевому току.

Как найти силу тока в каждом ответвлении параллельной цепи

Для расчёта силы тока в каждом проводнике параллельной цепи необходимо учитывать, что напряжение на всех элементах одинаково. Основное уравнение: I = U / R, где I – сила тока, U – напряжение, R – сопротивление ветви.

1. Измерьте общее напряжение источника питания. Оно будет одинаковым для всех параллельных ветвей.
2. Определите сопротивление каждого ответвления. Если в ветви несколько резисторов, рассчитайте их эквивалентное сопротивление по формуле:
   • Для последовательного соединения: R_экв = R₁ + R₂ + … + Rₙ
   • Для параллельного внутри ветви: 1/R_экв = 1/R₁ + 1/R₂ + … + 1/Rₙ
3. Вычислите ток в каждой ветви по формуле: I_ветви = U / R_ветви.

Пример: напряжение источника – 12 В. Ветвь 1 имеет сопротивление 4 Ом, ветвь 2 – 6 Ом. Тогда:

• Ветвь 1: I₁ = 12 В / 4 Ом = 3 А
• Ветвь 2: I₂ = 12 В / 6 Ом = 2 А

Суммарный ток в цепи: I = I₁ + I₂ = 5 А. Проверка по закону Кирхгофа: сумма токов в ветвях равна току на входе параллельной цепи.

Если сопротивления неизвестны, но известна мощность P каждого элемента, используйте формулу: I = √(P / R) или I = P / U при известном напряжении.

Применение закона Ома для участка цепи

Для расчёта силы тока в проводнике используется формула I = U / R, где I – ток (А), U – напряжение на участке цепи (В), R – сопротивление проводника (Ом). Если известны два из этих параметров, третий можно определить напрямую.

Например, при напряжении 12 В и сопротивлении 4 Ом сила тока составит 3 А. Такой расчёт применяется при анализе однородных участков цепи с постоянным сопротивлением. Если проводник состоит из нескольких резисторов, соединённых последовательно, сопротивления складываются: R_общ = R₁ + R₂ + … + R_n. Тогда ток на всём участке будет одинаковым и рассчитывается через общее сопротивление.

При параллельном соединении используется обратная сумма сопротивлений: 1/R_общ = 1/R₁ + 1/R₂ + … + 1/R_n. В этом случае напряжение на каждом элементе одинаково, а токи в ветвях рассчитываются индивидуально по закону Ома для каждой линии. Сумма этих токов даёт общий ток в узле.

Перед применением закона Ома необходимо удостовериться, что цепь находится в стационарном режиме и отсутствуют нелинейные элементы, искажающие зависимость тока от напряжения. В цепях с переменным током при наличии реактивных элементов дополнительно учитывается комплексное сопротивление.

Использование правил Кирхгофа для расчёта токов

Для анализа сложных электрических цепей с несколькими ветвями и узлами применяются два правила Кирхгофа: первое – правило узлов, и второе – правило контуров. Эти законы основаны на законе сохранения заряда и энергии и позволяют точно определить силу тока в каждом проводнике.

Первое правило Кирхгофа формулируется как: сумма токов, входящих в узел, равна сумме токов, выходящих из него. Это позволяет записать уравнение баланса токов для каждого узла схемы. Например, если к узлу подключены три проводника с токами I₁, I₂ и I₃, и I₁ и I₂ входят в узел, а I₃ выходит, то уравнение будет: I₁ + I₂ = I₃.

Второе правило Кирхгофа утверждает, что алгебраическая сумма напряжений в любом замкнутом контуре равна нулю. Это включает ЭДС и падения напряжения на резисторах. Для расчёта необходимо обозначить направление обхода контура и следовать правилу знаков: если ток направлен по обходу, то падение напряжения на резисторе R обозначается как -IR; если против – +IR. ЭДС обозначается положительной, если её направление совпадает с обходом, и отрицательной – в противном случае.

Для определения токов во всех ветвях составляют систему линейных уравнений на основе обоих правил. Количество уравнений по первому правилу равно количеству узлов минус один, по второму – количеству независимых контуров. Решение системы с помощью метода подстановки, Крамера или матричного метода позволяет получить значения всех токов.

Для повышения точности при составлении уравнений важно соблюдать одно направление обхода во всех контурах и не допускать арифметических ошибок. Рекомендуется предварительно обозначить все токи и напряжения на схеме, а затем пошагово записывать уравнения без пропусков.

Как учесть внутреннее сопротивление источника при расчётах

Внутреннее сопротивление источника (обозначается как R_вн) необходимо включать в расчёт, чтобы получить точные значения силы тока. Его учитывают, добавляя к нагрузке дополнительный резистор, соединённый последовательно с внешней цепью.

Для расчёта полной силы тока в цепи используется закон Ома в виде:

I = \(\frac{E}{R_{вн} + R_{н}}\),

где E – ЭДС источника, R_н – сопротивление внешней нагрузки.

Игнорирование R_вн приводит к завышению силы тока, особенно при малых значениях R_н. Например, при E = 12 В, R_н = 2 Ом и R_вн = 0,5 Ом, точный ток будет I = 12 / (2 + 0,5) = 4,8 А, вместо 6 А при расчёте без учёта внутреннего сопротивления.

При последовательном соединении нескольких источников внутренние сопротивления суммируются, что также влияет на общий ток. В таких случаях суммируйте все R_вн и прибавляйте к суммарному сопротивлению нагрузки.

При анализе сложных цепей с несколькими ветвями внутреннее сопротивление следует включать в эквивалентную схему источника перед вычислением токов в каждой ветви.

Для точных измерений внутреннее сопротивление рекомендуется определять экспериментально методом короткого замыкания или по вольтамперной характеристике источника, что позволяет избежать ошибок при расчётах.

Расчёт токов в смешанных соединениях резисторов

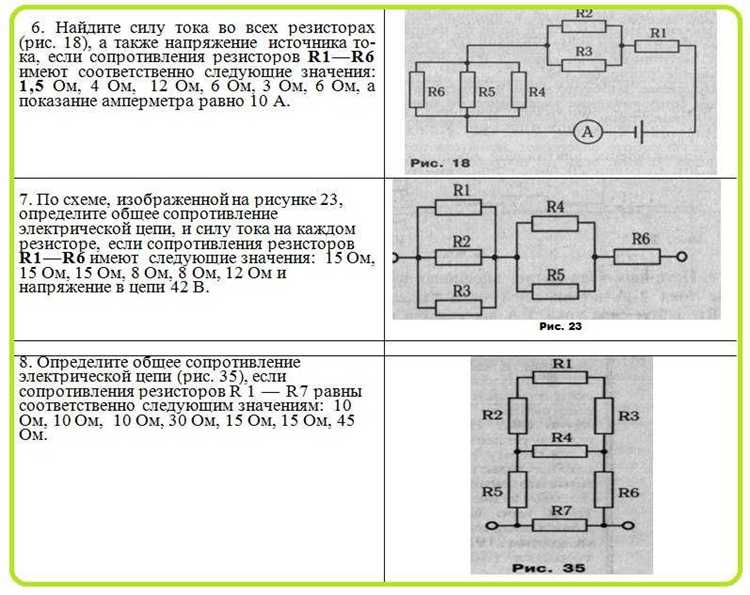
Смешанные соединения включают последовательное и параллельное объединение резисторов, что требует поэтапного анализа для определения токов в каждом проводнике.

1. Определить участки, соединённые последовательно и параллельно. Последовательное соединение характеризуется одинаковым током через все резисторы, параллельное – одинаковым напряжением на всех ответвлениях.
2. Рассчитать эквивалентное сопротивление для параллельных участков по формуле:
   1/R_экв = 1/R₁ + 1/R₂ + ... + 1/Rn. Для последовательных участков сопротивления суммируются:
   R_экв = R₁ + R₂ + ... + Rn.
3. Собрать эквивалентные сопротивления, последовательно сводя сложные участки, пока не получить общее сопротивление цепи.
4. По известному напряжению источника и общему сопротивлению найти полный ток цепи:
   I = U / R_экв.
5. Вернуться к разбиению цепи на исходные участки для вычисления токов в каждом проводнике:
   • В последовательной ветви ток одинаков для всех резисторов.
   • В параллельной ветви ток распределяется обратно пропорционально сопротивлениям:
     Iₖ = U_ветви / Rₖ, где U_ветви – напряжение на параллельном участке.
6. Проверить результаты, используя закон Кирхгофа: сумма токов на узле равна нулю, сумма падений напряжений в замкнутом контуре равна напряжению источника.

Рекомендуется использовать поэтапное упрощение схемы, избегая ошибок при вычислениях. При наличии сложных ветвлений эффективен метод контурных токов или узловых потенциалов.

Проверка расчётов с помощью баланса токов и напряжений

Для контроля точности расчётов тока в каждом проводнике необходимо применять закон Кирхгофа по току и напряжению. В узлах цепи сумма входящих токов должна равняться сумме исходящих. Проверка начинается с суммирования всех токов, подключенных к узлу, с учётом их направлений. Отклонение суммы от нуля не должно превышать 1–2% от максимального значения токов, что свидетельствует о корректности вычислений.

Для контуров цепи по второму закону Кирхгофа необходимо просуммировать напряжения всех элементов, включая источники и падения на сопротивлениях, следуя выбранному направлению обхода. Результат должен быть равен нулю с учётом погрешности измерений и вычислений не более 1%. При значительном расхождении проводится повторный анализ схемы и пересчёт параметров.

Практическая рекомендация – сначала выполнить расчёт токов, затем проверить узловой баланс, а после – контурный. Использование баланса напряжений подтверждает корректность направлений и величин токов. В сложных схемах с несколькими контурами рекомендуется проверять баланс по каждому контуру отдельно для выявления локальных ошибок.

Использование компьютерных симуляторов или программных средств расчёта помогает быстро выявлять нарушения баланса, однако понимание и самостоятельная проверка остаются обязательными для оценки достоверности результатов и исключения ошибок в исходных данных.

Вопрос-ответ:

Как определить силу тока в каждом проводнике сложной электрической цепи с несколькими ветвями?

Для вычисления силы тока в каждом проводнике необходимо применить закон Ома и правила Кирхгофа. Сначала составляют уравнения по первому закону Кирхгофа (закон сохранения тока), записывая сумму токов в узлах цепи. Затем применяют второй закон Кирхгофа (закон напряжений), составляют уравнения по замкнутым контурам. Решив систему уравнений, получают значения токов в каждом проводнике.

Почему сила тока в разных частях одной цепи может отличаться?

Если цепь имеет разветвления, ток делится между ними в зависимости от сопротивления каждого пути. Чем меньше сопротивление, тем большая часть тока проходит по этому проводнику. В последовательной цепи сила тока везде одинакова, но в параллельных ветвях она распределяется по-разному.

Можно ли вычислить силу тока в проводнике, не зная сопротивление других элементов цепи?

Нет, для точного расчёта силы тока в конкретном проводнике необходимо знать параметры всей цепи, так как ток зависит от общего сопротивления и конфигурации цепи. Без информации о других сопротивлениях и источниках напряжения определить ток нельзя.

Как влияет изменение сопротивления одного из проводников на ток в остальных частях цепи?

Изменение сопротивления одного из проводников влияет на распределение токов в цепи. В параллельных ветвях уменьшение сопротивления приводит к увеличению тока по этому пути и снижению токов в других ветвях. В последовательной цепи изменение сопротивления влияет на общий ток, меняя значения силы тока во всех элементах.

Какие методы упрощения электрических цепей используют для облегчения расчёта токов в проводниках?

Для упрощения часто используют замены параллельных и последовательных сопротивлений эквивалентными. Также применяют преобразование звезда-треугольник. Эти методы позволяют свести сложную цепь к более простой и рассчитать токи с меньшим количеством уравнений.

Как определить силу тока в каждом проводнике сложной электрической цепи с несколькими ветвями?

Для расчёта силы тока в каждом проводнике сложной цепи обычно применяют законы Кирхгофа: первый закон для определения суммарных токов в узлах и второй — для вычисления напряжений по замкнутым контурам. Сначала составляют уравнения на основе этих законов, учитывая сопротивления всех элементов. Решая полученную систему уравнений, получают значения токов в каждом участке цепи. Такой подход позволяет учесть влияние всех ответвлений и элементов на распределение токов.

Какие методы расчёта тока подходят для цепей с переменным током и как они отличаются от расчётов в цепях постоянного тока?

В цепях с переменным током для вычисления тока в проводниках используют методы, учитывающие комплексные сопротивления (импедансы), включающие активную и реактивную составляющие. Вместо простого закона Ома применяют комплексные формы выражений, где учитываются фазы напряжения и тока. Часто используются диаграммы векторных величин и комплексные числа. В отличие от цепей постоянного тока, здесь важна амплитуда и сдвиг по фазе, что требует применения более сложных математических инструментов.