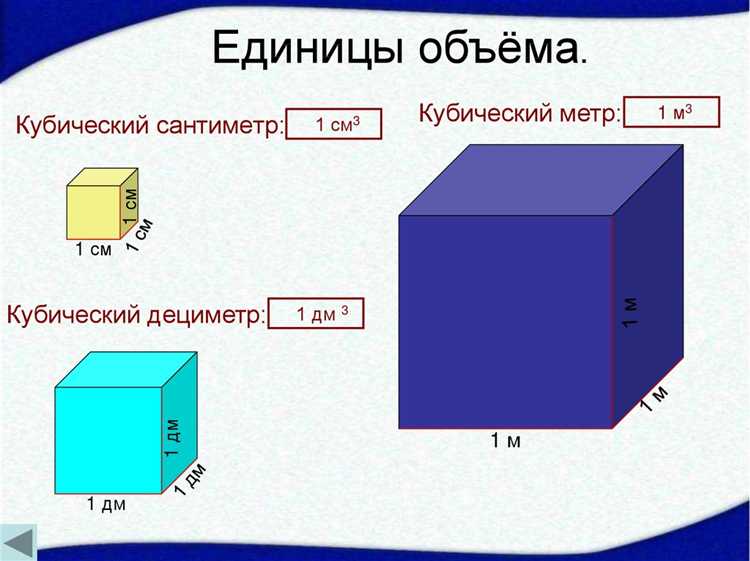
Объём в три кубических метра означает, что пространственная величина занимает 3 м³. При этом в вопросе «сколько метров в трёх кубических метрах» важно понимать, что метры – это единица длины, а кубические метры – единица объёма.
Если требуется узнать длину стороны куба с объёмом 3 м³, то длина будет равна корню кубическому из 3. Это примерно 1,442 метра. Такой подход применим только при равенстве всех измерений.
При вычислениях объёма важно учитывать форму и размеры объекта, так как объём может быть результатом произведения различных длины, ширины и высоты. Для практических задач с объёмом 3 м³ полезно использовать точные формулы и измерения, чтобы избежать ошибок в расчётах.
Что означает измерение в кубических метрах
Объём в кубических метрах важен при расчетах грузоподъёмности, объёма жидкостей, строительных материалов, а также для определения вместимости помещений и контейнеров. Для примера, 3 кубических метра – это объём трёх таких кубов, каждый со стороной 1 метр.
При пересчёте в метры линейные показатели теряют смысл, так как кубический метр – это не длина, а пространство. Поэтому вопрос «сколько метров в трёх кубических метрах» требует уточнения, в каком измерении или контексте необходимо получить результат.
Для точных расчетов объёма важно использовать все три измерения и помнить, что объем – произведение длины, ширины и высоты, выраженных в метрах. Это помогает избежать ошибок при планировании и оценке физических характеристик объектов.
Как перевести кубические метры в метры линейные
Формула объема прямоугольного параллелепипеда: V = длина × ширина × высота. Если известен объем и две из трёх линейных мер, то третью можно найти через деление:
Линейная мера = Объем (м³) ÷ (Известная линейная мера 1 × Известная линейная мера 2)
Например, при объеме 3 м³ и известных размерах основания 1 м на 0,5 м:
Высота = 3 ÷ (1 × 0,5) = 6 метров.
Если объект имеет форму куба, все стороны равны, значит:
Сторона = кубический корень из объема. Для 3 м³ это примерно 1,442 м.
Без дополнительных данных о форме или размерах объекта напрямую перевести кубические метры в линейные невозможно.
Роль формы объекта при расчёте длины из объёма
Объём выражается в кубических единицах и учитывает три измерения: длину, ширину и высоту. Чтобы определить длину по известному объёму, необходимо учитывать форму объекта. Например, если объект – куб, длина ребра вычисляется как кубический корень из объёма. Для объёма 3 м³ длина ребра будет примерно 1,442 м, так как ∛3 ≈ 1,442.
Если объект – прямоугольный параллелепипед с известными двумя сторонами, длину можно найти, разделив объём на произведение этих сторон. Например, при объёме 3 м³ и ширине 1 м, высоте 0,5 м длина равна 3 / (1 × 0,5) = 6 м.
Для цилиндров длина высоты рассчитывается как объём, делённый на площадь основания. При радиусе основания 0,5 м и объёме 3 м³ высота равна 3 / (π × 0,5²) ≈ 3,82 м.
Форма определяет формулу расчёта длины. Без точного знания формы невозможно корректно определить длину по объёму. Рекомендация – сначала чётко определить геометрию объекта, затем использовать соответствующую формулу для вычисления линейного размера.
Пример расчёта длины стороны куба из трёх кубометров
Объём куба равен произведению длины стороны на себя трижды: V = a³. Для объёма 3 м³ уравнение выглядит так: a³ = 3.
Чтобы найти длину стороны a, нужно извлечь кубический корень из 3:
a = ∛3 ≈ 1,442 м.
Это значит, что куб с объёмом 3 кубических метра имеет длину стороны около 1,442 метра.
Для точности измерений рекомендуется использовать калькулятор с функцией извлечения корней или специализированное ПО.
Как определить длину трубы из заданного объёма
Для расчёта длины трубы по известному объёму необходимо учитывать внутренний диаметр трубы. Формула объёма цилиндра:
V = π × r² × L,
где V – объём трубы, r – внутренний радиус, L – длина.
Для нахождения длины выразим её из формулы:
L = V / (π × r²).
- Измерьте внутренний диаметр трубы (d).
- Вычислите радиус: r = d / 2.
- Подставьте значение радиуса и объём (в кубических метрах) в формулу.
- Вычислите длину L в метрах.
Пример: задан объём 3 м³, диаметр трубы 0,3 м.
- r = 0,3 / 2 = 0,15 м
- L = 3 / (3.1416 × 0,15²) ≈ 3 / (3.1416 × 0,0225) ≈ 3 / 0,0707 ≈ 42,45 м
Таким образом, длина трубы с внутренним диаметром 0,3 м и объёмом 3 м³ составит примерно 42,45 метра.
Особенности перевода объёма в длину для прямоугольных объектов
Объём прямоугольного параллелепипеда рассчитывается по формуле V = длина × ширина × высота. Чтобы определить длину при известном объёме, необходимо фиксировать или задавать значения ширины и высоты.
Если известен объём, например, 3 м³, и заданы ширина и высота, длина находится как L = V / (ширина × высота). При ширине 0,5 м и высоте 0,6 м длина будет L = 3 / (0,5 × 0,6) = 10 м.
Без конкретных данных о двух других размерах определить длину однозначно невозможно, поскольку объём – трёхмерная характеристика, а длина – одномерная.
Для точного перевода объёма в длину рекомендуется использовать фиксированные параметры с точностью не менее миллиметра, чтобы избежать значительных ошибок, особенно при малых габаритах.
При расчётах важно учитывать единицы измерения: если объём задан в кубических метрах, все размеры должны быть в метрах для корректности вычислений.
При необходимости перехода от объёма к длине для объектов с переменной толщиной или шириной стоит применять усреднённые значения, полученные экспериментально или из технических условий.
Как использовать плотность материала для расчёта длины по объёму
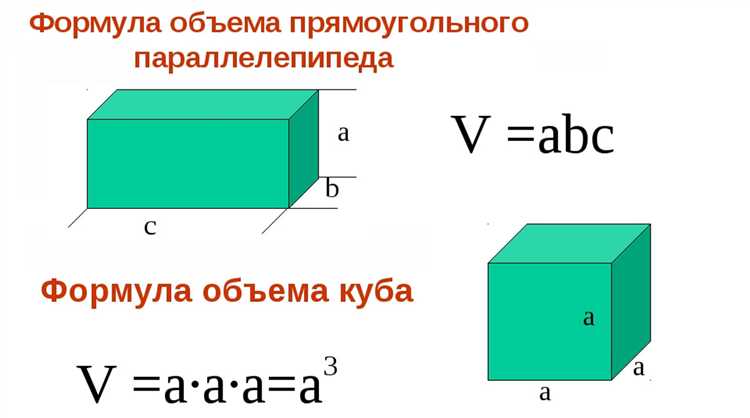
Для вычисления длины объекта при известном объёме и плотности необходимо учитывать форму и сечение материала. Объём (V) равен произведению площади поперечного сечения (S) на длину (L): V = S × L. Если площадь сечения известна, длину можно найти как L = V / S.
Плотность (ρ) связана с массой (m) и объёмом формулой ρ = m / V. Зная массу и плотность, можно определить объём: V = m / ρ.
Комбинируя формулы, при известной массе и площади сечения длина вычисляется так: L = m / (ρ × S). Это позволяет определить длину, исходя из массы и свойств материала.
Например, если масса металлической полосы равна 10 кг, плотность стали около 7850 кг/м³, а площадь сечения 0,002 м², длина будет: L = 10 / (7850 × 0,002) ≈ 0,64 м.
В случае отсутствия точных данных по площади сечения следует измерить её или использовать стандартизированные размеры для данного типа материала.
Важно учитывать, что точность результата зависит от точности измерений массы, площади и плотности, а также от однородности материала.
Практические задачи: измерение длины из объёма в строительстве и ремонте
Объём материалов часто измеряется в кубических метрах, но для расчётов нужны линейные размеры. Чтобы перевести объём в длину, необходимо учитывать форму и площадь поперечного сечения объекта.
Основные формулы и подходы:
- Если известен объём V (м³) и площадь сечения S (м²), длина L (м) вычисляется по формуле: L = V / S.
- Для прямоугольных конструкций площадь сечения – произведение ширины на высоту.
- Для круглых труб или стержней площадь сечения – π × (радиус)².
Примеры задач:
- Необходимо определить длину бетонного блока объёмом 3 м³, если площадь его поперечного сечения 0,5 м²: L = 3 / 0,5 = 6 м.
- Расчёт длины металлической трубы при объёме 3 м³ и внутреннем радиусе 0,1 м: S = π × 0,1² ≈ 0,0314 м²; L = 3 / 0,0314 ≈ 95,54 м.
Рекомендации при работе с объёмами и длинами:
- Точно измеряйте площадь сечения перед вычислениями – малейшая ошибка увеличивает погрешность длины.
- Учитывайте особенности материала: например, для сыпучих материалов полезно знать плотность и степень уплотнения.
- При сложных формах используйте разбиение на простые геометрические фигуры для более точного расчёта площади сечения.
- Для ремонта, где длина влияет на расход отделочных материалов, рекомендуется применять данные расчёты для контроля затрат и планирования.
Вопрос-ответ:
Что означает измерение в кубических метрах, и как оно связано с длиной в метрах?
Кубический метр — это единица объёма, которая описывает пространство в трёх измерениях: длине, ширине и высоте. Один кубический метр — это объём куба со сторонами по одному метру. Метры, в свою очередь, — это длина, измеряемая в одном измерении. Поэтому просто сказать, сколько метров в кубических метрах, нельзя без указания конкретного направления или преобразования в длину по одной из сторон.
Можно ли напрямую перевести три кубических метра в метры? Если нет, почему?
Нет, напрямую перевести объём в метры длины нельзя, потому что кубический метр — это объём, а метр — это длина. Чтобы получить длину из объёма, нужно знать, как распределён этот объём. Например, если у нас куб с объёмом 3 кубических метра, длина его стороны будет равна кубическому корню из 3, то есть примерно 1,44 метра. Без дополнительной информации просто число «3 кубических метра» не даёт длину.
Если у меня есть 3 кубических метра воды, как можно определить длину одной из сторон ёмкости, в которой она хранится?
Для определения длины стороны ёмкости, нужно знать форму и размеры других сторон. Если ёмкость — куб, то длина стороны будет равна кубическому корню из объёма: кубический корень из 3 приблизительно 1,44 метра. Если форма другая, например, прямоугольная призма, то длину можно найти, разделив объём на произведение других двух измерений. Например, если ширина и высота по 1 метр, длина будет 3 метра.
Как понять, почему объём измеряется в кубических метрах, а длина — в метрах?
Объём — это пространство, занимаемое предметом, и выражается через три измерения: длину, ширину и высоту. Если каждое из этих измерений измеряется в метрах, то объём получается в кубических метрах (м³), что означает умножение трёх длины. Длина — это только одно измерение, поэтому её измеряют в метрах. Разница в единицах отражает разницу между одномерной и трёхмерной величинами.
Можно ли представить 3 кубических метра как длину, если изменить форму объекта?
Да, если известна форма объекта, то можно выразить длину одной из сторон, исходя из объёма. Например, если взять длинный прямоугольный параллелепипед, у которого ширина и высота очень малы, а объём 3 м³, то длина будет очень большой, поскольку объём равен произведению всех трёх измерений. Если форма меняется, длина тоже меняется, но объём остаётся 3 м³. Таким образом, длина и объём связаны через форму и размеры объекта.