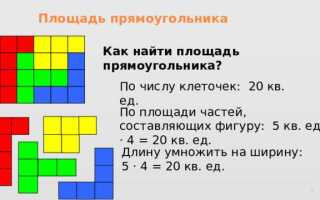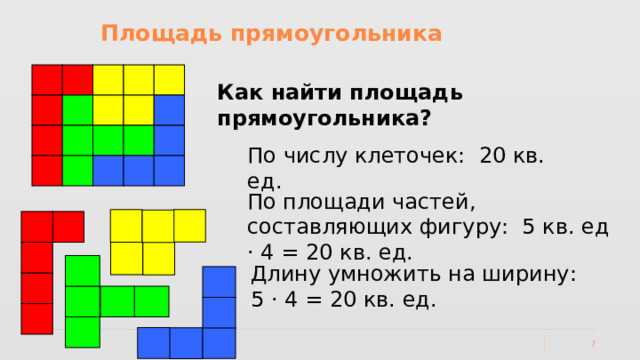
Для прямоугольных и квадратных поверхностей расчет площади сводится к простому умножению длины на ширину. Если длина составляет 5 метров, а ширина – 3 метра, площадь вычисляется как 5 × 3 = 15 м². Этот метод применим ко всем объектам с прямыми углами – от комнат до участков земли.
Перед расчетом необходимо убедиться, что обе величины указаны в одинаковых единицах. Если длина задана в метрах, а ширина – в сантиметрах, необходимо привести их к одной системе: 1 м = 100 см. Например, длина 4 м и ширина 250 см преобразуются в 4 м и 2,5 м. Площадь будет 4 × 2,5 = 10 м².
При использовании нестандартных единиц, таких как дюймы или футы, нужно сначала перевести их в метры или другую удобную величину. Один фут равен 0,3048 метра, один дюйм – 2,54 сантиметра. После перевода применяется та же формула.
Если измерения проводятся вручную, точность имеет значение. Лучше использовать рулетку с миллиметровой шкалой и фиксировать размеры до одного знака после запятой. При проектировании помещений допустимая погрешность обычно не превышает 1 см на 10 м.
Формула вычисления площади прямоугольника

Площадь прямоугольника определяется по формуле: S = a × b, где a – длина, b – ширина. Оба значения должны быть выражены в одной системе единиц (например, в метрах).
Если длина прямоугольника составляет 5 метров, а ширина – 3 метра, то площадь равна: 5 × 3 = 15 м². При работе с сантиметрами, результат будет в квадратных сантиметрах: 500 см × 300 см = 150 000 см².
При измерении с помощью рулетки фиксируйте длину и ширину с точностью до миллиметра, затем переводите значения в метры перед подстановкой в формулу. Это обеспечит корректный итог в квадратных метрах.
Если один из параметров неизвестен, вычисление невозможно. Обязательно наличие двух величин – длины и ширины.
Формула применима только к фигурам с прямыми углами. Для других форм используется иной подход.
Как измерить длину и ширину комнаты рулеткой
Перед началом измерений освободите пространство вдоль стен от мебели и предметов, которые могут мешать точному замеру.
- Возьмите рулетку с фиксатором полотна. Длина полотна должна быть не менее 5 метров для стандартных помещений.
- Выберите одну из длинных стен комнаты. Один человек удерживает нулевую отметку рулетки в углу у стены на уровне пола, второй протягивает полотно до противоположной стены, удерживая его строго горизонтально.
- Приложите край рулетки как можно ближе к стене, избегая изгибов и провисания. Измерение считывается в месте соприкосновения полотна с противоположной стеной. Запишите полученное значение с точностью до миллиметра.
- Повторите процедуру для широкой стороны комнаты. При необходимости произведите измерение в нескольких точках, если стены неровные. Фиксируйте наименьшее значение.
- Если комната имеет нишу или выступ, измерьте каждую часть отдельно и суммируйте полученные длины или ширины.
Не полагайтесь на визуальные оценки – даже незначительное отклонение может привести к неправильному расчёту площади.
Что делать, если длина и ширина даны в разных единицах
Для точного расчёта площади необходимо привести длину и ширину к одной системе измерения. Игнорирование этого шага приведёт к неверному результату. Например, если длина указана в метрах, а ширина в сантиметрах, то одна из величин должна быть преобразована.
Преобразование выполняется через соотношения: 1 м = 100 см, 1 см = 10 мм, 1 м² = 10 000 см². Если длина 3 м, а ширина 250 см, то длину переводим в сантиметры: 3 м × 100 = 300 см. После этого площадь рассчитывается: 300 см × 250 см = 75 000 см².
Если данные указаны в дюймах и метрах, используем конвертацию: 1 дюйм = 2,54 см, 1 м = 39,37 дюйма. При длине 5 футов и ширине 2 м: 5 футов × 30,48 = 152,4 см; 2 м = 200 см. Площадь: 152,4 см × 200 см = 30 480 см².
Единицы площади зависят от выбранной системы. Если преобразование выполнено в метры, результат получится в м². Если в сантиметры – в см². Нельзя складывать разные единицы в одном выражении – всегда приводите всё к одной.
При использовании калькулятора убедитесь, что единицы указаны корректно. Многие онлайн-инструменты автоматически конвертируют значения, но лучше проверять вручную, особенно при нестандартных величинах, таких как ярды, дюймы или футы.
Как рассчитать площадь участка неправильной формы через разбиение на прямоугольники

Для начала нанесите границы участка на бумагу или в графическом редакторе, сохранив масштаб. Разбейте фигуру на несколько прямоугольников так, чтобы каждый из них охватывал часть территории без перекрытий.
Измерьте длину и ширину каждого прямоугольника. Для точности используйте лазерный дальномер или рулетку. Запишите размеры всех прямоугольников, полученных при разбиении.
Рассчитайте площадь каждого прямоугольника по формуле: площадь = длина × ширина. Например, если один из фрагментов имеет размеры 5 м на 8 м, его площадь будет 40 м².
Сложите площади всех прямоугольников: Sобщ = S1 + S2 + S3 + … + Sn, где n – количество участков. Результат даст общую площадь исходного участка.
Для контроля сверяйте итоговую форму с исходной схемой. Если участок остался неучтенным, разбейте его на дополнительные прямоугольники и пересчитайте.
Точность расчёта зависит от правильности разбиения: чем ближе форма фрагментов к прямоугольникам и меньше их число, тем выше точность и меньше погрешность.
Подсчёт площади с округлением до нужной точности

Для вычисления площади прямоугольной поверхности необходимо перемножить длину и ширину: S = длина × ширина. Например, при длине 5,784 м и ширине 3,267 м площадь составит 18,910728 м².
Чтобы округлить результат, определите требуемую точность. При округлении до двух знаков после запятой используйте правило математического округления. В приведённом примере: 18,910728 округляется до 18,91 м².
Если требуется округлить до целых, результат – 19 м². Для округления до тысячных: 18,911 м². Используйте формат округления, соответствующий контексту задачи: для инженерных расчётов – до трёх или четырёх знаков, для бытовых нужд – один или два.
При работе с миллиметрами предварительно переведите значения в метры (например, 5784 мм = 5,784 м), иначе получите площадь в мм², что затруднит последующее округление.
Для автоматизации используйте формулу в электронных таблицах: =ОКРУГЛ(длина * ширина; n), где n – число знаков после запятой. Это исключает ручные ошибки и обеспечивает точность.
Расчёт площади в квадратных метрах для закупки материалов
Для точного расчёта количества строительных и отделочных материалов необходимо знать площадь помещения или отдельного элемента. Используется формула: длина × ширина = площадь в м².
- Если нужно покрыть пол: измерьте длину и ширину комнаты по внутренним стенам. Например, комната 5,2 м × 3,8 м = 19,76 м².
- Для стен: измерьте высоту и длину каждой стены, умножьте и сложите площади всех стен. Вычтите площадь дверей и окон.
- При закупке ламината, плитки или ковролина учитывайте запас 5–10 % на подрезку и брак.
- Для фасадных или кровельных материалов уточняйте, измеряется ли полезная площадь листа или общая. Например, профнастил 1,1 м шириной имеет полезную ширину 1 м – при расчёте это критично.
- Сначала выполните точные замеры рулеткой, записывая значения до сантиметра.
- Рассчитайте площадь по каждой поверхности отдельно: стены, потолок, пол.
- Сложите результаты и добавьте процент на запас в зависимости от материала.
- Проверьте единицы измерения – площадь должна быть в квадратных метрах, упаковка материалов может указываться в м², погонных метрах или штуках.
Если форма помещения нестандартная, разбивайте её на простые прямоугольники и рассчитывайте каждый участок отдельно, затем суммируйте. Для укладки кафеля в нишах или углах учтите дополнительный запас до 15 %.
Как найти площадь в квадратных сантиметрах для мелких объектов
Для измерения площади небольших предметов, таких как монеты, кнопки или детали ручной работы, потребуется линейка с миллиметровой шкалой или штангенциркуль. Важно измерять с точностью до миллиметра, так как даже небольшая погрешность может существенно повлиять на результат.
Если объект имеет прямоугольную форму, используйте формулу:
Площадь (см²) = Длина (см) × Ширина (см)
Пример: если длина объекта 2,3 см, а ширина 1,5 см, то:
Площадь = 2,3 × 1,5 = 3,45 см²
Для круглых предметов используется формула:
Площадь (см²) = π × (Диаметр / 2)²
Пример: диаметр монеты – 1,8 см. Тогда:
Площадь = 3,14 × (0,9)² ≈ 2,54 см²
Если форма сложная, разбейте объект на геометрические фигуры и вычислите площадь каждой отдельно, затем сложите полученные значения.
Рекомендуется производить измерения на твердой поверхности, плотно прижимая объект к линейке. Измеряйте несколько раз для минимизации погрешностей и используйте среднее значение.
Распространённые ошибки при вычислении площади по длине и ширине

Ошибка в единицах измерения – одна из самых частых. Если длина указана в метрах, а ширина в сантиметрах, результат будет некорректным. Перед вычислением приведите все значения к одной системе: либо метры, либо сантиметры.
Неверное понимание формулы. Некоторые пользователи по ошибке складывают длину и ширину, а затем умножают результат на два, принимая эту формулу за определение площади. Правильное вычисление: площадь = длина × ширина.
Округление данных до расчёта. Преждевременное округление длины или ширины может привести к значительной погрешности. Используйте исходные значения с максимальной точностью, округляя результат только на финальном этапе.
Пренебрежение реальными размерами. В строительстве или при заказе материалов часто указываются номинальные размеры, которые могут отличаться от фактических. Используйте только реальные размеры, измеренные вручную.
Игнорирование особенностей формы объекта. Прямоугольная формула подходит только для объектов с прямыми углами. Если форма нестандартная (трапеция, треугольник, окружность), применяйте соответствующие формулы, иначе площадь будет рассчитана неверно.
Неправильный порядок действий. Иногда при автоматизированных расчётах (например, в Excel) забывают расставить скобки, из-за чего нарушается логика вычислений. Убедитесь, что формула прописана правильно: =A1*A2, а не =(A1+A2)*2.
Вопрос-ответ:
Как узнать площадь, если известны только длина и ширина?
Если у вас есть длина и ширина, то площадь можно найти, перемножив эти два значения. Формула простая: площадь = длина × ширина. Например, если длина комнаты 5 метров, а ширина — 3 метра, то площадь будет 5 × 3 = 15 квадратных метров.
Можно ли использовать эту формулу для измерения площади дачного участка?
Да, если участок имеет прямоугольную или квадратную форму, то формула длина × ширина подойдет. Например, если участок 20 метров в длину и 10 метров в ширину, площадь будет 200 квадратных метров. Если участок имеет неправильную форму, стоит разбить его на прямоугольные части, посчитать их площади отдельно и сложить.
А как перевести полученную площадь в другие единицы измерения?
Чтобы перевести площадь, например, из квадратных метров в квадратные сантиметры, нужно умножить результат на 10 000 (поскольку в одном квадратном метре 10 000 см²). Для перевода в квадратные километры — делите на 1 000 000. Аналогично работает перевод и в другие единицы, главное — знать соотношение между ними.
Что делать, если длина и ширина указаны в разных единицах?
В таком случае сначала нужно привести обе величины к одним и тем же единицам. Например, если длина указана в метрах, а ширина — в сантиметрах, ширину нужно перевести в метры, разделив на 100. Только после этого можно использовать формулу для расчета площади. Иначе результат получится некорректным.
Если у помещения есть ниша или выступ, как учесть их при расчете площади?
В этом случае удобнее всего разделить помещение на несколько прямоугольных участков. Посчитайте площадь каждого участка отдельно, затем сложите результаты. Например, если есть основная часть комнаты 4×5 метров и ниша 1×2 метра, сначала получаем 20 м², потом 2 м². Общая площадь — 22 м². Такой способ позволяет учитывать сложные формы без потери точности.