Как найти силу тока в цепи переменного тока

Определение силы тока в цепях переменного тока требует учета не только сопротивления, как в постоянных цепях, но и таких параметров, как индуктивность и емкость. Эти элементы создают реактивное сопротивление, которое влияет на фазовый сдвиг между напряжением и током. Для расчета используется полное сопротивление Z, определяемое как векторная сумма активного R и реактивного сопротивления X, где X = X_L — X_C.

Формула для расчета силы тока имеет вид: I = U / Z, где I – сила тока в амперах, U – действующее значение напряжения в вольтах, Z – модуль полного сопротивления в омах. При наличии индуктивности и емкости Z = √(R² + (X_L — X_C)²). Здесь X_L = 2πfL – индуктивное сопротивление, X_C = 1 / (2πfC) – емкостное сопротивление, f – частота, L – индуктивность, C – емкость.

Рассматривая бытовую сеть с частотой 50 Гц и напряжением 220 В, подключение катушки индуктивности с L = 0.1 Гн и отсутствием активного сопротивления приведет к X_L ≈ 31.4 Ом. Тогда I = 220 / 31.4 ≈ 7 А. Добавление параллельного конденсатора с C = 100 мкФ уменьшит реактивное сопротивление, так как X_C ≈ 31.8 Ом, что почти компенсирует X_L, приводя Z к минимуму и увеличивая ток.

Для точного расчета необходимо учитывать фазовый угол между напряжением и током, особенно в цепях с комбинированной нагрузкой. Использование комплексных чисел и векторных диаграмм позволяет не только вычислить силу тока, но и определить активную, реактивную и полную мощность цепи. Это критично при проектировании и диагностике электроустановок с переменным током.

Как определить амплитуду тока при известном напряжении и сопротивлении

Для расчета амплитуды тока в цепи переменного тока требуется знать амплитудное значение напряжения и активное сопротивление участка цепи. Используется формула:

I_м = U_м / R,

где I_м – амплитуда тока в амперах, U_м – амплитуда напряжения в вольтах, R – сопротивление в омах.

Если известно только действующее значение напряжения, необходимо сначала определить амплитуду напряжения по формуле:

U_м = √2 × U_д,

где U_д – действующее (эффективное) значение напряжения. Например, при напряжении 220 В амплитуда составит около 311 В.

Подставляя полученное значение в первую формулу, можно точно рассчитать амплитуду тока. Например, при U_д = 220 В и R = 100 Ом:

I_м = (√2 × 220) / 100 ≈ 3,11 А.

Важно учитывать, что указанный подход применим только к цепям с чисто активной нагрузкой. При наличии индуктивности или ёмкости сопротивление следует заменить на полное (импеданс).

Расчет тока в цепи с активным, индуктивным и емкостным сопротивлениями

Для расчета тока в цепи переменного тока с активным (R), индуктивным (L) и емкостным (C) сопротивлениями необходимо определить полное сопротивление цепи – полную комплексную величину, называемую импедансом (Z). Импеданс рассчитывается по формуле: Z = √(R² + (X_L — X_C)²), где X_L = ωL – индуктивное сопротивление, X_C = 1 / (ωC) – емкостное сопротивление, ω = 2πf – круговая частота, f – частота тока в Гц.

После определения импеданса, ток I в цепи находится как I = U / Z, где U – действующее значение напряжения источника. Важно учитывать фазовый сдвиг между током и напряжением, который определяется разностью X_L и X_C. При X_L > X_C ток отстает по фазе, при X_L < X_C – опережает.

Пример: при R = 20 Ом, L = 0,1 Гн, C = 100 мкФ и f = 50 Гц: ω = 2π × 50 ≈ 314 рад/с, X_L = 31,4 Ом, X_C ≈ 31,8 Ом. Z = √(20² + (31,4 — 31,8)²) ≈ √(400 + 0,16) ≈ 20,004 Ом. При U = 220 В ток составит I ≈ 220 / 20,004 ≈ 11 А.

Для уменьшения реактивного сопротивления и повышения коэффициента мощности применяют компенсацию: подбором конденсаторов или катушек добиваются X_L ≈ X_C, минимизируя мнимую часть импеданса и увеличивая активную мощность.

Определение мгновенного значения тока по уравнению синусоиды

Мгновенное значение тока в цепи переменного тока рассчитывается по уравнению:

i(t) = I_m · sin(ωt + φ)

Где: I_m – амплитуда тока (максимальное значение), ω – циклическая частота (рад/с), t – время в секундах, φ – начальная фаза (в радианах).

Для получения точного результата подставляют известные значения. Например, при I_m = 5 А, f = 50 Гц (следовательно, ω = 2πf = 314 рад/с), φ = 0 и t = 0,01 с, расчет выглядит так:

i(0,01) = 5 · sin(314 · 0,01) = 5 · sin(3,14) ≈ 5 · 0,0016 ≈ 0,008 А

Если начальная фаза не равна нулю, ее необходимо учитывать. Например, при φ = π/2 мгновенное значение тока будет сдвинуто по фазе:

i(t) = I_m · sin(ωt + π/2) = I_m · cos(ωt)

В этом случае удобно использовать косинус вместо синуса. Подстановка данных проводится аналогично.

Для высокоточной работы важно, чтобы все значения были приведены к согласованным единицам измерения (амперы, секунды, радианы). Ошибки округления и некорректный учет фазы приводят к искажению расчета.

Как рассчитать ток в цепи с резонансом напряжений

Резонанс напряжений возникает в последовательной RLC-цепи при совпадении частоты источника с собственной частотой контура. В этом режиме реактивные сопротивления индуктивности и емкости компенсируют друг друга, и суммарное сопротивление цепи минимально – равно активному сопротивлению R.

Чтобы точно рассчитать ток при резонансе, следуйте следующему алгоритму:

Определите параметры цепи: сопротивление R (в Омах), индуктивность L (в Генри), емкость C (в Фарадах).
Вычислите резонансную частоту по формуле:
f₀ = 1 / (2π√(LC))
Убедитесь, что частота источника переменного тока совпадает с f₀. Только в этом случае наступает резонанс.
Вычислите полное сопротивление цепи:

Z = R (поскольку X_L = X_C и их сумма равна нулю)
Рассчитайте силу тока по закону Ома:

I = U / R, где U – действующее значение напряжения источника.

Дополнительные рекомендации:

При резонансе ток достигает максимального значения, поэтому важно учитывать тепловые потери и допустимый ток элементов.
Индуктивная и емкостная реактивности должны быть точно подобраны. Малейшее отклонение от расчетной частоты уменьшит ток в цепи.
Если известна добротность контура Q, то ток можно также выразить как:

I = Q·I_рез, где I_рез – ток на резонансной частоте при заданном напряжении.

Использование комплексных чисел для расчета тока в цепи переменного тока

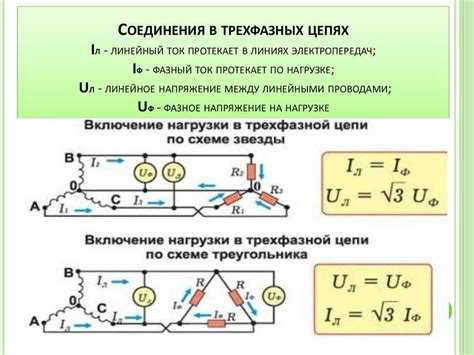
В цепях переменного тока напряжение и ток описываются синусоидальными функциями, отличающимися по фазе. Для удобства анализа вводится понятие комплексного сопротивления (импеданса), обозначаемого как Z = R + jX, где R – активное сопротивление, X – реактивное, j – мнимая единица.

Расчет тока осуществляется по аналогии с законом Ома: I = U / Z, где U – комплексное напряжение, Z – комплексное сопротивление. Если, например, U = 230∠0° В, а Z = 10 + j5 Ом, то I = 230∠0° / √(10² + 5²)∠arctg(5/10) = 230∠0° / 11.18∠26.57° = 20.57∠−26.57° А.

Комплексный ток содержит как амплитуду, так и фазовый сдвиг, что позволяет точно определить активную и реактивную составляющие мощности. Для этого используется формула S = U × I*, где I* – комплексно-сопряженный ток. При этом активная мощность P = Re(S), реактивная – Q = Im(S).

Важный момент: при расчете цепей с несколькими элементами необходимо складывать импедансы алгебраически. Например, для последовательного соединения катушки (Z_L = jωL) и резистора (R) общее сопротивление Z = R + jωL. При параллельном соединении используется формула 1/Z = 1/Z₁ + 1/Z₂.

Использование комплексных чисел позволяет применять методы векторной алгебры, упрощая расчет фазовых соотношений и амплитуд в цепях с различными элементами. Это особенно важно при проектировании фильтров, согласующих цепей и в системах с несинусоидальными сигналами, где требуется спектральный анализ с применением преобразования Фурье.

Расчет силы тока при наличии трансформатора в цепи

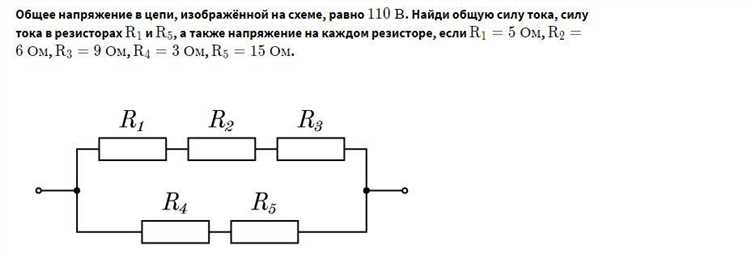
Для расчета силы тока на стороне трансформатора необходимо учитывать соотношение напряжений и токов первичной и вторичной обмоток. Если известна мощность нагрузки S (в вольт-амперах) и напряжение вторичной обмотки U₂, ток на вторичной стороне определяется по формуле:

I₂ = S / U₂

Ток на первичной стороне I₁ связан с током вторичной стороны через коэффициент трансформации, равный отношению напряжений k = U₁ / U₂:

I₁ = I₂ / k

Где U₁ – номинальное напряжение первичной обмотки. При практическом расчете важно учитывать, что токи изменяются обратно пропорционально напряжению, а мощность трансформатора сохраняется (за исключением потерь).

Если мощность задана в ваттах и известен коэффициент мощности нагрузки cos φ, активный ток рассчитывается как I = P / (U × cos φ). Для реактивных или сложных нагрузок необходимо дополнительно учитывать фазовый угол, используя комплексные числа.

При подключении трансформатора в цепь переменного тока рекомендуют предварительно замерить напряжение и учитывать допуски на потери в обмотках – обычно 1–3%. Это обеспечивает точность расчета силы тока и предотвращает перегрузки.

Как найти ток в параллельной цепи с разными типами сопротивлений

В параллельной цепи с переменным током каждая ветвь может содержать резисторы, индуктивности и емкости. Для точного расчёта тока важно учитывать комплексное сопротивление (импеданс) каждой ветви.

Определение импеданса ветви
- Резистор: \( Z_R = R \)
- Индуктивность: \( Z_L = j \omega L \), где \( \omega = 2 \pi f \)
- Емкость: \( Z_C = \frac{1}{j \omega C} \)
Вычисление полного импеданса ветви
Если ветвь содержит несколько элементов, соединённых последовательно, суммируйте их импедансы:

\( Z_{\text{ветви}} = Z_1 + Z_2 + … + Z_n \)
Определение токов в каждой ветви
Общее напряжение на всех ветвях одинаково и равно \( U \). Ток в ветви рассчитывается по формуле:

\( I_i = \frac{U}{Z_i} \), где \( Z_i \) – комплексный импеданс i-й ветви.
Расчёт полной силы тока цепи
Полный ток цепи находится как векторная сумма токов всех ветвей:

\( I_{\text{общий}} = \sum I_i \)
Практические рекомендации
- Используйте комплексные числа для вычисления импедансов и токов.
- При частоте 50 или 60 Гц рассчитывайте \( \omega \) соответственно.
- При наличии нескольких ветвей с реактивными элементами обязательно учитывайте фазовый сдвиг токов.
- Проверяйте результат с помощью закона Кирхгофа для токов: сумма токов в узле равна нулю.

Проверка правильности расчета силы тока с помощью фазорных диаграмм

Фазорная диаграмма позволяет визуализировать соотношение между напряжением, током и реактивными составляющими цепи переменного тока. Для проверки расчетов силы тока необходимо построить фазоры напряжения (U), активного сопротивления (R), индуктивного (X_L) и емкостного (X_C) сопротивлений.

Расчетная величина силы тока I определяется по формуле:

I = U / Z, где Z = √(R² + (X_L — X_C)²)

После вычисления модуля тока строят фазор тока под углом φ, где φ = arctg((X_L — X_C) / R). Угол φ соответствует сдвигу фаз между напряжением и током.

Для проверки результата на фазорной диаграмме:

Постройте горизонтальный вектор напряжения U.
Нанесите вектор активного сопротивления R по направлению тока.
Отложите вектор реактивного сопротивления X = X_L — X_C перпендикулярно к R (вверх для индуктивной, вниз – для емкостной нагрузки).
Результирующий вектор Z – диагональ прямоугольного треугольника, построенного на R и X.
Вектор тока I должен быть направлен под углом φ к U, обратным по отношению к углу Z.

Если угол и модуль вектора I совпадают с расчетными значениями, вычисления корректны. Несовпадение указывает на ошибку в определении составляющих сопротивления или неверный учет фазовых сдвигов.

Практическое применение: при измерениях с помощью осциллографа или фазометра можно сопоставить экспериментальные данные с построенной диаграммой. Расхождение более 5% требует пересмотра исходных параметров.

Вопрос-ответ:

Как определить амплитудное значение тока в цепи переменного напряжения?

Амплитудное значение тока — это максимальное значение, которое ток достигает за один период колебания. Чтобы найти его, нужно знать мгновенное значение тока и использовать соответствующую формулу. В случае синусоидального тока амплитуда равна произведению максимального напряжения на проводимость цепи с учётом её сопротивления и реактивных элементов.

Почему для расчёта тока в цепи переменного тока учитывают не только сопротивление, но и реактивные элементы?

В цепях переменного тока присутствуют не только резисторы, но и конденсаторы с катушками индуктивности, которые создают реактивное сопротивление. Оно влияет на фазу тока относительно напряжения и изменяет общую величину тока. Поэтому для точного расчёта необходимо учитывать комплексное сопротивление, состоящее из активного и реактивного компонентов.

Какие методы используются для вычисления тока в сложных цепях с несколькими источниками и элементами?

Для расчёта тока в таких цепях применяют методы анализа переменного тока, например, метод комплексных сопротивлений, метод наложения, или вычисление с помощью фазорных диаграмм. Иногда применяют численные методы и программные средства для анализа, учитывающие все параметры элементов и их взаимное влияние.

Как влияет частота переменного напряжения на величину тока в цепи?

Частота влияет на реактивное сопротивление элементов: индуктивное сопротивление увеличивается с ростом частоты, а емкостное — уменьшается. Это меняет общее сопротивление цепи и, соответственно, величину тока. При высоких частотах индуктивные элементы могут сильно ограничивать ток, а при низких — роль емкостных становится менее заметной.