Какую способность диэлектрика в эл поле характеризует диэлектрическая проницаемость

Диэлектрическая проницаемость – ключевой параметр, определяющий реакцию вещества на внешнее электрическое поле. Этот показатель отражает способность материала поляризоваться, тем самым экранируя внутреннюю область от действия поля. Проницаемость обозначается как ε и входит в уравнение связи между напряжённостью поля E и электрическим смещением D: D = εE.

Абсолютная диэлектрическая проницаемость измеряется в фардах на метр (Ф/м) и зависит от молекулярной структуры вещества. Для вакуума она постоянна: ε₀ ≈ 8,854×10⁻¹² Ф/м. Относительная проницаемость определяется как ε_r = ε / ε₀ и варьируется от единицы (вакуум) до сотен (например, у титаната бария при комнатной температуре ε_r достигает 1000 и более).

Для практического применения материалов важно учитывать частотную зависимость проницаемости. В низкочастотном диапазоне поляризация возникает за счёт ориентации молекул и ионной подвижности. С ростом частоты эти механизмы ослабевают, и проницаемость уменьшается. Для высокочастотной техники применяются материалы с минимальной дисперсией, например фторопласт (ε_r ≈ 2.1).

Температурный фактор также влияет на ε: при повышении температуры подвижность диполей увеличивается, но при определённой границе поляризация разрушается, что ведёт к снижению проницаемости. Для стабильной работы в электронике применяют термостойкие диэлектрики с низким температурным коэффициентом проницаемости, например слюду и керамики на основе оксида алюминия.

Выбор диэлектрика по проницаемости должен учитывать как величину ε, так и потери, выраженные через тангенс угла диэлектрических потерь. Высокая проницаемость эффективна при создании компактных конденсаторов, но сопровождается ростом потерь, если не оптимизирован состав материала.

Как определить диэлектрическую проницаемость вещества в лабораторных условиях

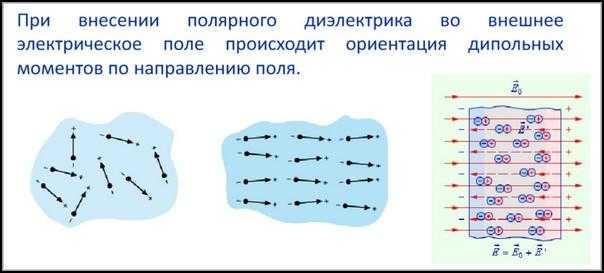
Определение диэлектрической проницаемости (ε) основывается на измерении емкости конденсатора с образцом диэлектрика между электродами и сравнении с емкостью без образца.

Подготовка образца:
- Изготовьте плоскую пластину из исследуемого материала с толщиной от 0,1 до 1 мм, обеспечив параллельность поверхностей.
- Очистите поверхность от загрязнений и обеспечьте плотный контакт с электродами.
Сборка измерительной схемы:
- Используйте конденсатор с плоскими параллельными электродами, расстояние между которыми равно толщине образца.
- Подключите измерительный прибор – мост переменного тока или LCR-метр, позволяющий измерять емкость с точностью не хуже 0,1%
Измерения:
- Измерьте емкость конденсатора без образца (C₀), чтобы получить эталонное значение.
- Установите образец между электродами и измерьте емкость (C).
- Для точности измерений контролируйте температуру и влажность, так как они влияют на результаты.
Расчет диэлектрической проницаемости:
- Используйте формулу ε = C / C₀, где C – емкость с диэлектриком, C₀ – емкость без диэлектрика.
- При необходимости учитывайте геометрические параметры конденсатора и образца для корректировки расчетов.

Для точных исследований применяют также метод импедансного анализа, позволяющий получить комплексную диэлектрическую проницаемость с учётом потерь и фазовых сдвигов. При работе с жидкими диэлектриками используют измерительные ячейки с калибровкой по стандартным образцам.

Связь между молекулярной поляризуемостью и диэлектрической проницаемостью

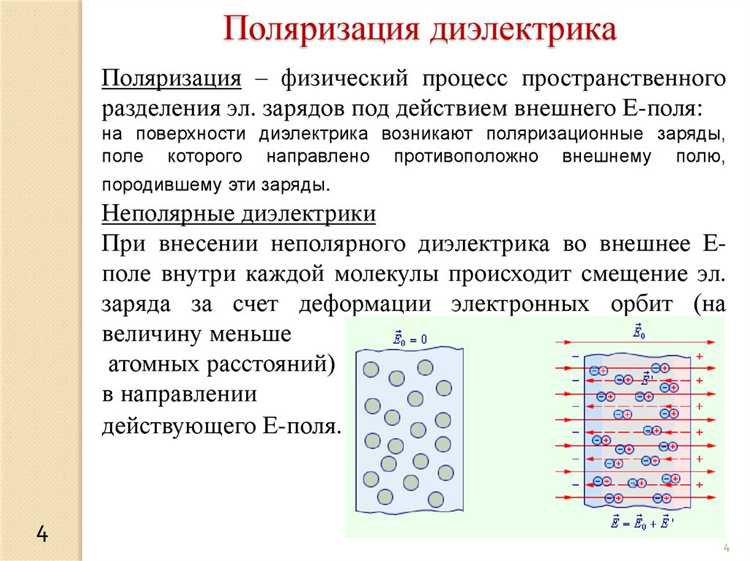
Диэлектрическая проницаемость вещества ε напрямую связана с микроскопической характеристикой – молекулярной поляризуемостью α. Связь между этими величинами описывается уравнением Клаузиуса – Моссотти:

(ε — 1) / (ε + 2) = (4πNα) / 3

Здесь N – число молекул в единице объема. Это выражение позволяет оценить диэлектрические свойства среды, зная поляризуемость её компонентов. При этом важно учитывать, что уравнение справедливо только для изотропных и разреженных сред, где взаимодействие между диполями минимально.

Молекулярная поляризуемость α зависит от электронной структуры молекулы и характеризует её способность деформироваться под действием внешнего электрического поля. Чем больше α, тем выше вклад каждой молекулы в макроскопическую поляризацию среды, а следовательно, и в ε.

Для расчёта α рекомендуется использовать квантово-химические методы, такие как теория функционала плотности (DFT), особенно при анализе сложных органических молекул и полимеров. Экспериментально α определяется по данным о преломлении и плотности с применением уравнения Лоренца – Лоренца.

В системах с высокой плотностью молекул необходимо учитывать коррекции на межмолекулярные взаимодействия. Игнорирование коллективных эффектов приводит к переоценке проницаемости. В таких случаях следует применять методы молекулярной динамики или модель локального поля.

Повышение диэлектрической проницаемости композита возможно путём подбора компонентов с высокой α и оптимальной ориентацией молекул. Практически это реализуется в материалах с упорядоченной структурой, например, в жидкокристаллических и ферроэлектрических средах.

Роль диэлектрической проницаемости в расчетах ёмкости конденсаторов

Ёмкость плоского конденсатора определяется формулой \( C = \varepsilon_0 \varepsilon_r \frac{S}{d} \), где \( \varepsilon_0 \) – электрическая постоянная (8,854×10⁻¹² Ф/м), \( \varepsilon_r \) – относительная диэлектрическая проницаемость, \( S \) – площадь обкладок, \( d \) – расстояние между ними. Именно параметр \( \varepsilon_r \) напрямую влияет на возможность увеличения ёмкости без изменения геометрии устройства.

Например, при использовании диэлектрика с \( \varepsilon_r = 10 \) ёмкость увеличивается в 10 раз по сравнению с вакуумом. В высокоёмкостных керамических конденсаторах применяют материалы с \( \varepsilon_r \) до 10 000, что позволяет существенно снизить размеры при сохранении нужной ёмкости.

При проектировании важно учитывать температурную стабильность \( \varepsilon_r \). У ферроэлектриков она резко меняется при переходе через точку Кюри, что критично в прецизионной электронике. В таких случаях предпочтение отдают материалам с минимальным температурным коэффициентом проницаемости.

Также следует учитывать частотную зависимость. При высоких частотах \( \varepsilon_r \) может снижаться, что уменьшает фактическую ёмкость. Поэтому в ВЧ-технике выбирают диэлектрики с низкой диэлектрической дисперсией, например, PTFE или кварц с \( \varepsilon_r \approx 2 \).

В импульсных цепях предпочтительны материалы с высокой пробивной прочностью и малым тангенсом угла потерь, чтобы избежать перегрева и снижения эффективности. Подбор диэлектрика должен базироваться не только на значении \( \varepsilon_r \), но и на совокупности его электрических, температурных и механических свойств.

Как выбрать материал с нужной проницаемостью для радиотехнических применений

При выборе диэлектрика для радиотехнических устройств необходимо учитывать диэлектрическую проницаемость (ε), стабильность параметров в диапазоне рабочих частот и температур, а также потери (tg δ). Для ВЧ и СВЧ-диапазонов предпочтительны материалы с ε в пределах 2–10 и минимальными потерями – tg δ менее 10⁻³.

В антеннах и радиопрозрачных покрытиях важна низкая ε – от 2 до 4. Это снижает искажения волнового фронта и уменьшает отражения. Распространённые материалы: политетрафторэтилен (ε ≈ 2,1), полистирол (ε ≈ 2,5), пенополиэтилен (ε ≈ 1,6–1,9).

Для СВЧ-резонаторов и фильтров, наоборот, выбирают керамики с высокой ε – от 10 до 100. Это уменьшает размеры компонентов. Примеры: титант бария (ε ≈ 1200), титанат магния (ε ≈ 17), цирконат-станнат бария (ε ≈ 30–40).

Для подложек печатных плат применяются стеклотекстолиты (ε ≈ 4,5), Rogers (ε ≈ 2,2–10), керамики (ε ≈ 6–100). Выбор зависит от частоты, точности согласования и тепловых характеристик. Для частот выше 10 ГГц предпочтительны материалы с термостабильной ε и tg δ ниже 0,001.

Нельзя полагаться только на паспортные данные. Реальные параметры могут отличаться в зависимости от партии, влажности и метода обработки. Рекомендуется проводить ВЧ-измерения на образцах в условиях, близких к рабочим.

Влияние температуры и влажности на изменение проницаемости диэлектриков

Диэлектрическая проницаемость материалов чувствительна к внешним условиям, в частности к температуре и влажности. Эти параметры критически влияют на стабильность и надежность диэлектрических свойств, особенно в точной электронике и системах высокого напряжения.

Температура: С увеличением температуры усиливаются тепловые колебания молекул, что изменяет поляризуемость вещества. Для большинства полярных диэлектриков проницаемость ε увеличивается до определённого порога, после чего наблюдается спад вследствие термической деструкции структурных связей.
Для неполярных материалов, таких как политетрафторэтилен (ПТФЭ), ε практически не изменяется до температур выше 200 °C, после чего снижается из-за деградации молекулярной решётки.
У керамических диэлектриков на основе титаната бария (BaTiO₃) наблюдается пик проницаемости вблизи точки Кюри (~120 °C), за которым следует резкое падение ε, связанное с фазовым переходом из ферроэлектрического в параэлектрическое состояние.

Влажность: Гигроскопичные материалы, такие как эпоксидные компаунды, активно поглощают влагу из воздуха. В результате образуются проводящие каналы, что увеличивает кажущуюся проницаемость и одновременно снижает сопротивление изоляции.
Увлажнение может привести к ионизации примесей внутри структуры диэлектрика, особенно при напряжениях выше 1 кВ, что ускоряет старение материала и приводит к пробою.
Для предотвращения влияния влажности рекомендуется использовать влагонепроницаемую упаковку, применять осушители в корпусах и избегать хранения диэлектриков при относительной влажности выше 60 %.

Практическая рекомендация: при проектировании систем, работающих в широком температурном диапазоне или во влажной среде, необходимо учитывать температурный коэффициент проницаемости и влагостойкость используемого материала. Регулярное тестирование ε при различных условиях позволяет выявить отклонения до начала деградации изоляции.

Методы измерения относительной диэлектрической проницаемости в промышленности

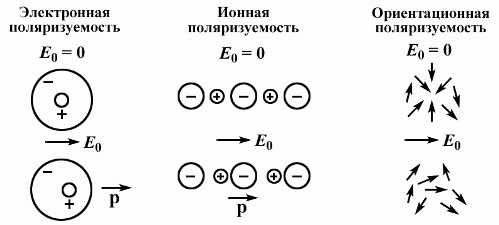
В промышленной практике для определения относительной диэлектрической проницаемости (ε_r) применяются приборы и методики, обеспечивающие точность в диапазоне от 1,001 до 10⁴ в зависимости от типа материала. Наиболее распространены три метода: мостовой, резонансный и коаксиально-волноводный.

Мостовой метод основан на применении измерительных мостов переменного тока. Используется в диапазоне частот до 1 МГц. Пример – мост Шеринга, позволяющий определить ε_r твердых и жидких диэлектриков с погрешностью до ±1%. Образец размещается между плоскими электродами, образующими конденсатор, емкость которого сравнивается с эталонной.

Резонансный метод применяется для высокочастотных измерений (от 1 МГц до 30 ГГц). В основе – измерение сдвига резонансной частоты полости при внесении образца. Метод обеспечивает высокую чувствительность (до ±0,1%) и применяется для керамик, полимеров и покрытий в диапазоне 2–100 ε_r. Важным фактором является геометрическая стабильность образца.

Коаксиально-волноводный метод используется при частотах от 1 ГГц и выше, особенно для тонких пленок и диэлектрических покрытий. Метод основан на измерении коэффициента отражения и пропускания электромагнитной волны через материал, помещённый в измерительную линию. Используется анализатор цепей (VNA) и специализированная калибровка (TRL или SOLT). Погрешность метода составляет 1–5% в зависимости от частоты и свойств материала.

Для повышения достоверности результатов в условиях производства рекомендуется:

Проводить калибровку оборудования перед каждой серией измерений.
Контролировать влажность и температуру образцов, особенно для гигроскопичных материалов.
Применять образцы строго установленной геометрии.
Проводить измерения в диапазоне частот, соответствующем области применения материала.

Ошибки при интерпретации значений проницаемости и как их избежать

Ошибка 1: Принятие относительной диэлектрической проницаемости за постоянную. Во многих справочниках указывается значение ε_r при частоте 1 кГц и температуре 20 °C. Однако при изменении частоты и температуры значение ε_r может существенно меняться. Например, для диэлектрика типа ПВХ ε_r может снижаться на 30–40 % при повышении частоты до 1 МГц. Учитывайте рабочие условия: частотный диапазон, температурный режим и наличие внешних полей.

Ошибка 2: Игнорирование потерь в материале. При расчётах часто используют только значение ε_r, забывая о наличии мнимой части комплексной проницаемости (ε = ε′ – jε″). Особенно в ВЧ-диапазоне потери (ε″) становятся критичными. Так, керамика типа Y5V при 100 кГц имеет ε′ ≈ 10 000, но при этом тангенс угла потерь достигает 0,1, что делает её непригодной для точных схем. В расчётах обязательно используйте комплексное представление проницаемости.

Ошибка 3: Использование табличных значений без учёта технологических допусков. Производственные отклонения могут достигать ±20 % для одних и тех же марок материалов. Например, для фторопласта ε_r в разных партиях варьируется от 2,0 до 2,2. При критичных приложениях (СВЧ, прецизионная электроника) необходимо проводить индивидуальные измерения проницаемости образцов из каждой партии.

Ошибка 4: Пренебрежение анизотропией материалов. В слоистых композиционных диэлектриках, таких как стеклотекстолит или ориентированные полимеры, ε_r в плоскости слоя и перпендикулярно ему может различаться на 15–50 %. При проектировании СВЧ-структур или печатных плат всегда уточняйте направление измерения и используйте данные, соответствующие конкретной геометрии поля.

Рекомендации: Используйте данные измерений, выполненных в условиях, максимально приближенных к рабочим. При работе в переменных температурных и частотных режимах применяйте модели, учитывающие дисперсию ε. При необходимости рассчитывайте ε экспериментально с помощью мостовых или резонансных методов. Избегайте слепого копирования справочных значений без контекста применения.