Частота резонанса определяется параметрами конкретной системы – массой, жесткостью и демпфированием. В механических системах с одной степенью свободы она рассчитывается по формуле f = (1/2π)·√(k/m), где k – коэффициент жесткости, m – масса. При изменении этих величин резонансная частота смещается, что влияет на устойчивость и безопасность конструкции.
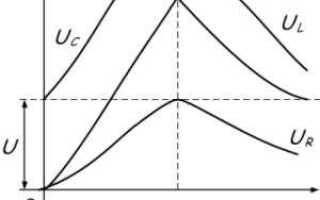
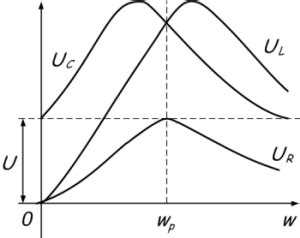
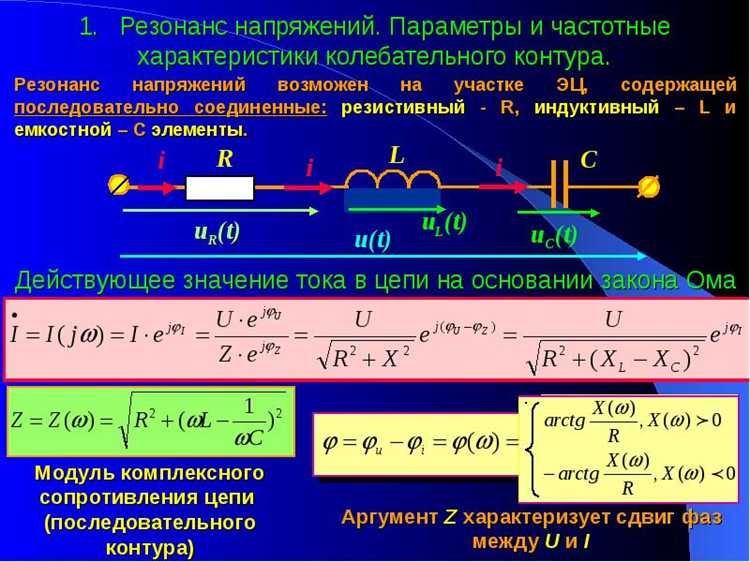
В электрических цепях резонанс возникает при равенстве реактивных сопротивлений индуктивности и емкости: ω₀ = 1/√(LC). Здесь L – индуктивность, C – емкость. Точный расчет и настройка параметров критичны для минимизации потерь и повышения качества сигнала.
Для систем с несколькими степенями свободы резонансные частоты образуют спектр, соответствующий собственным колебаниям. Оптимизация конструкции требует учета всех значимых мод, что позволяет избегать нежелательных вибраций и повреждений.
Практическая рекомендация – использовать методы экспериментального определения резонанса, такие как анализ частотной характеристики, в сочетании с численным моделированием. Это обеспечивает более точное понимание динамики и позволяет контролировать влияние изменений параметров на рабочие характеристики систем.
Определение резонансной частоты в механических колебательных системах
Резонансная частота механической системы определяется как частота, при которой амплитуда вынужденных колебаний достигает максимума. Для классической модели гармонического осциллятора с массой m и жесткостью пружины k резонансная частота ω₀ вычисляется по формуле:
ω₀ = √(k / m).
В системах с демпфированием резонансная частота смещается и может быть найдена как:
ω_r = √(k / m — (c / 2m)²),
где c – коэффициент вязкого трения. Для точного определения резонансной частоты рекомендуется использовать спектральный анализ колебаний или метод частотного сканирования с фиксацией амплитуды.
В многозвенных системах резонансные частоты вычисляются через собственные значения матриц жесткости и масс. Для практических задач целесообразно применять численные методы, например, метод конечных элементов или модальный анализ, чтобы получить спектр собственных частот и выявить резонансные режимы.
Важно учитывать влияние внешних факторов, таких как изменение массы, жесткости и демпфирования, на сдвиг резонансной частоты. Рекомендуется проводить экспериментальную калибровку для повышения точности расчетов и предотвращения нежелательных вибраций в конструкциях.
Расчёт частоты резонанса в электрических цепях с индуктивностью и ёмкостью
Частота резонанса в цепях, содержащих индуктивность (L) и ёмкость (C), определяется формулой:
f₀ = 1 / (2π √(L·C)), где f₀ – резонансная частота в герцах (Гц), L – индуктивность в генри (Гн), C – ёмкость в фарадах (Ф).
Для точного вычисления необходимо учитывать реальное значение индуктивности и ёмкости, измеренные с помощью LCR-метра, поскольку номиналы компонентов могут отличаться от паспортных. При проектировании рекомендуется учитывать допуски компонентов для оценки возможного диапазона резонансной частоты.
В случае параллельного или последовательного соединения индуктивности и ёмкости резонанс возникает, когда реактивные сопротивления взаимно компенсируются. В последовательной цепи это соответствует минимальному импедансу, в параллельной – максимальному.
При расчёте учитывайте влияние сопротивления катушки и утечек в конденсаторе, что влияет на добротность и может смещать частоту резонанса. Для повышения точности применяйте комплексный анализ цепи с учётом потерь.
Для практических задач рекомендуется проводить моделирование в специализированных программах (например, SPICE), что позволяет учесть нелинейности и паразитные эффекты, недоступные при простом аналитическом расчёте.
Влияние демпфирования на резонансную частоту в пружинно-массовых системах
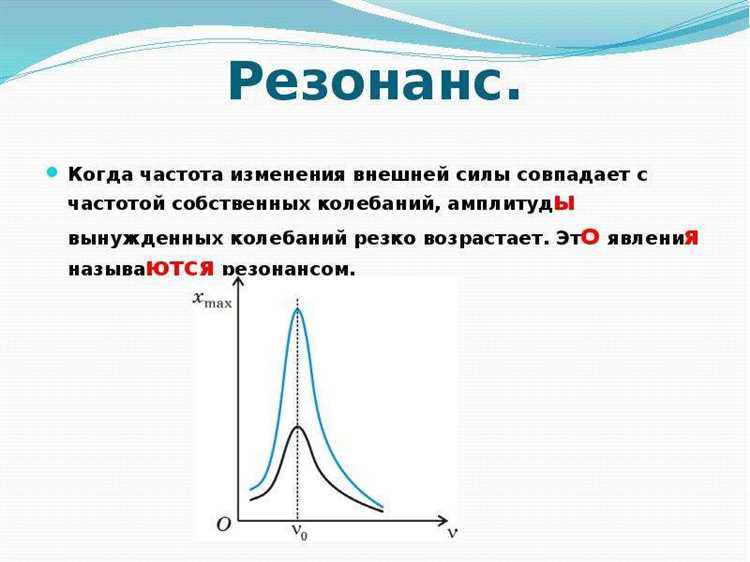
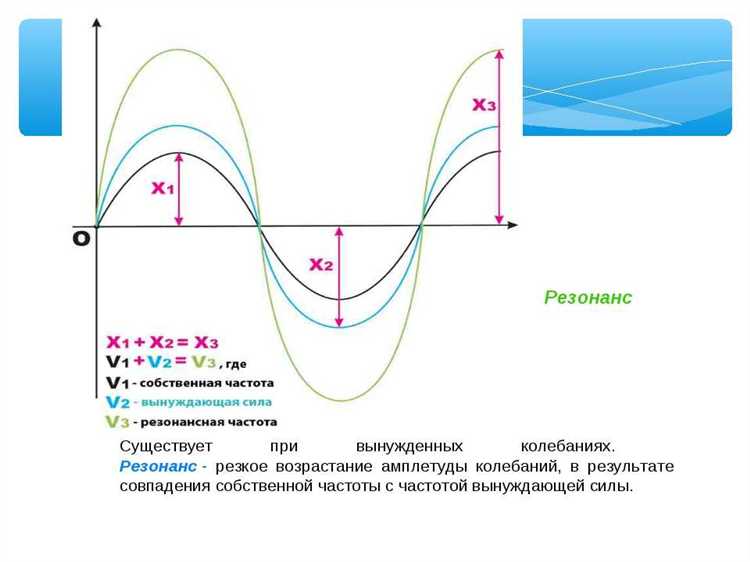
В пружинно-массовой системе с демпфированием резонансная частота смещается относительно собственной частоты без затухания. Её можно определить по формуле: ω_r = ω_0 √(1 — 2ζ²), где ω_0 – собственная частота системы, ζ – коэффициент демпфирования. При малых значениях ζ смещение резонансной частоты незначительно, однако при ζ > 0,1 наблюдается заметное снижение ω_r.
Демпфирование уменьшает амплитуду колебаний на резонансе, снижая нагрузку на конструктивные элементы. Для практического расчёта оптимального ζ рекомендуется исходить из допустимого уровня вибраций и требований к быстродействию системы. Значения ζ от 0,05 до 0,2 часто обеспечивают баланс между амплитудой и скоростью затухания.
При проектировании систем с активным управлением демпфированием важно учитывать, что увеличение ζ ведёт к понижению резонансной частоты и изменению фазового сдвига между силой и откликом. Это влияет на точность синхронизации и эффективность передачи энергии.
В системах с нелинейными характеристиками пружины или демпфера изменение ζ может вызывать дополнительные эффекты, включая появление побочных резонансов и изменение спектра частот. В таких случаях расчет резонансной частоты требует численных методов и экспериментальной валидации.
Для снижения влияния демпфирования на резонансную частоту при сохранении гашения колебаний применяют комбинации пассивных и активных демпферов, позволяющих поддерживать стабильные характеристики системы в широком диапазоне нагрузок.
Частота резонанса в акустических системах и её практическое применение
Частота резонанса в акустических системах определяется параметрами колебательной среды, включая геометрию резонатора и свойства материала. Для открытых труб она рассчитывается по формуле f = v / (2L), где v – скорость звука в среде, L – длина трубы. В закрытых трубах частота резонанса определяется формулой f = v / (4L).
В акустических колонках резонанс влияет на качество звука, особенно в области низких частот. Корпус с резонансной частотой ниже 40 Гц помогает улучшить басы, однако чрезмерное усиление резонансных пиков ведёт к искажениям. Для подавления нежелательных резонансов применяются демпфирующие материалы и фазоинверторные порты, которые изменяют параметры резонатора.
В архитектурной акустике учёт резонансных частот позволяет избежать нежелательных стоячих волн, вызывающих резонансные провалы и пики в спектре помещения. Для этого проводят расчёты и измерения частот с использованием методов импульсного отклика и корректируют конструкции с помощью звукопоглощающих панелей и диффузоров.
В музыкальных инструментах резонанс обеспечивает усиление определённых гармоник, что формирует характерный тембр. Например, в струнных инструментах корпус настроен на частоты от 200 до 1000 Гц для оптимального звучания. В духовых инструментах изменение длины воздушного столба изменяет резонансные частоты, что используется для настройки нот.
Практическое применение частоты резонанса включает проектирование звуковых фильтров, настройку микрофонов и громкоговорителей, а также контроль вибраций в помещениях и оборудованиях. Точный расчёт и корректировка резонансных параметров позволяют повысить качество передачи и восприятия звука.
Изменение резонансной частоты в системах с переменной массой или жёсткостью

Резонансная частота колебательной системы определяется формулой \( f_0 = \frac{1}{2\pi} \sqrt{\frac{k}{m}} \), где \(k\) – коэффициент жёсткости, \(m\) – масса. При изменении массы или жёсткости происходит смещение резонансной частоты.
В системах с переменной массой увеличение \(m\) приводит к уменьшению частоты, пропорционально корню из обратного значения массы. Например, удвоение массы снижает резонансную частоту примерно на 29%. Для точного расчёта учитывают динамическое распределение массы, особенно если изменение происходит неравномерно.
Изменение жёсткости оказывает более прямое влияние: рост \(k\) увеличивает частоту по корню из значения жёсткости. Удвоение жёсткости повышает частоту примерно на 41%. В инженерных конструкциях жёсткость может меняться вследствие температурных воздействий, износа материалов или изменения нагрузки, что требует постоянного мониторинга.
В системах с одновременно изменяющейся массой и жёсткостью рекомендуется использовать численные методы для оценки резонансных характеристик, так как аналитические решения становятся сложными. Метод конечных элементов и анализ собственных значений позволяют выявить новые частоты и моды колебаний.
Для управления резонансной частотой в таких системах применяют регулируемые демпферы, изменяемые механические компоненты или активные системы адаптации параметров. Это снижает риск возникновения резонансных перегрузок и улучшает стабильность работы.
Методы измерения резонансной частоты в вибрационном анализе оборудования
Для определения резонансной частоты в вибрационных системах применяют следующие методы:
- Анализ спектра вибрации – запись вибрационного сигнала с помощью акселерометров и последующий анализ частотного спектра с помощью БПФ (быстрого преобразования Фурье). Максимумы амплитуды указывают на резонансные частоты.
- Импульсное воздействие – короткий удар по корпусу оборудования с фиксацией отклика вибрации. Этот метод позволяет выделить собственные частоты и режимы колебаний без длительного нагружения.
- Синусоидальное воздействие – применение вибратора с плавным изменением частоты (частотный скан). По величине амплитуды отклика выявляют резонанс.
- Анализ переходной характеристики – измерение отклика системы на ступенчатое воздействие, что позволяет выявить частоты, на которых наблюдается значительное увеличение амплитуды.
- Определение частот методом случайного возбуждения – регистрация отклика при случайных или промышленно-неизбежных вибрациях, с последующим спектральным анализом.
Рекомендуется применять комбинированный подход для повышения точности. Для оборудования с известной конструкцией предпочтителен импульсный или синусоидальный методы, обеспечивающие контроль параметров возбуждения. В случаях сложных систем с несколькими степенями свободы целесообразен анализ случайного возбуждения с продвинутой обработкой сигналов.
Критично правильно закрепить датчики и обеспечить минимальный уровень шума. Частотный диапазон регистрации должен превышать ожидаемую резонансную частоту минимум в 1,5 раза для выявления близких гармоник.
Применение резонансной частоты для диагностики дефектов в механизмах
Резонансная частота служит ключевым параметром при выявлении механических повреждений и износа в деталях оборудования. Изменение резонансных характеристик указывает на изменение физических свойств конструкции – массы, жесткости, демпфирования.
В вибродиагностике измеряют собственные частоты колебаний узлов и элементов. Появление дополнительных резонансных пиков или сдвиг главной резонансной частоты на 5–10% свидетельствует о растрескивании, ослаблении креплений или дефектах подшипников. Например, при проверке валов смещение частоты более чем на 3 Гц от эталонного значения требует немедленного анализа.
Методика основана на воздействии контролируемых вибраций с переменной частотой и регистрации амплитуды отклика. Для точной диагностики используют спектральный анализ с разрешением не менее 0,1 Гц. Важен учет температуры и эксплуатационных условий, так как они влияют на частотные характеристики.
Рекомендации для внедрения диагностики:
- Регулярный мониторинг резонансных частот позволяет отслеживать динамические изменения состояния оборудования.
- Использование портативных виброметров с функцией FFT ускоряет выявление аномалий.
- Определение базовых частот при заводских испытаниях обеспечивает точную привязку для последующего сравнения.
- Комбинирование данных резонанса с другими методами (ультразвук, тепловизор) повышает точность диагностики.
Таким образом, анализ резонансной частоты обеспечивает раннее обнаружение дефектов, снижая риск аварий и увеличивая ресурс механизмов.
Особенности резонансных частот в биологических системах и медицинских приборах
Резонансные частоты в биологических тканях зависят от плотности, вязкости и электромеханических свойств клеток. Это используется при диагностике и терапии, включая МРТ, УЗИ и электромагнитную стимуляцию.
- В МРТ основная резонансная частота зависит от гиромагнитного отношения протонов: при напряжённости магнитного поля 1,5 Тл частота составляет около 63,87 МГц, при 3 Тл – 127,74 МГц.
- При ультразвуковом исследовании применяются частоты от 2 до 15 МГц. Более высокие значения дают лучшее разрешение, но снижают глубину проникновения, что важно при исследовании сосудов, щитовидной железы, мягких тканей.
- Тканевая импедансная томография учитывает частотный отклик клеточных мембран: в диапазоне 10 кГц – 10 МГц различаются здоровые и патологические структуры по диэлектрическим свойствам.
- В нейростимуляции и терапии боли (TENS, rTMS) применяются частоты от 1 до 100 Гц. Для подавления корковой активности – 1 Гц, для стимуляции – 10–20 Гц. Эти параметры подбираются с учётом типа ткани и цели воздействия.
- Микроволновая диатермия использует частоты 915 МГц и 2,45 ГГц, обеспечивая локальный нагрев тканей. Резонанс возникает при совпадении длины волны с размером структур, повышая эффективность поглощения.
При разработке медицинских приборов необходимо учитывать резонансные свойства тканей, чтобы избежать перегрева, искажения сигнала или неэффективного воздействия.
- Определять диапазоны резонансных частот конкретных тканей в заданных условиях (температура, влажность, давление).
- Использовать частотную модуляцию для обхода нежелательных резонансов в соседних структурах.
- Проверять взаимодействие с имплантами и металлическими конструкциями, которые могут смещать резонансные пики.
Игнорирование этих факторов может привести к диагностическим ошибкам или повреждению тканей при терапии.