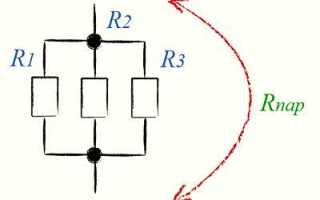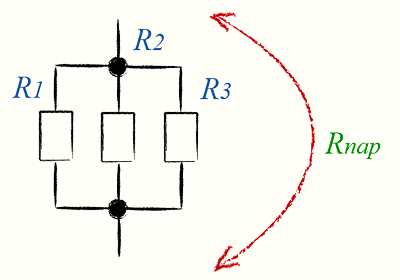
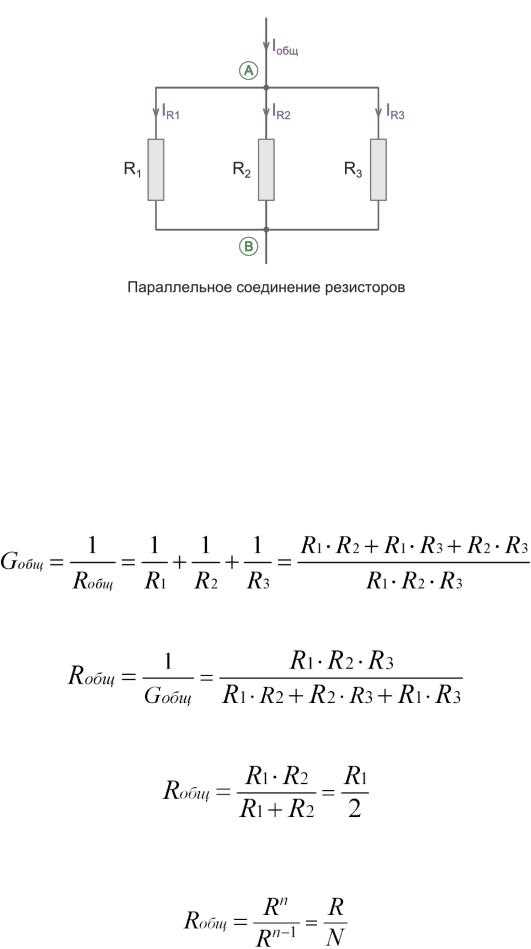
При параллельном соединении резисторов общее сопротивление рассчитывается по специальной формуле, которая отличается от расчета в случае последовательного соединения. Важно понимать, что при параллельном соединении резисторы создают пути для тока, и каждый из них влияет на общую проводимость цепи. Для расчета сопротивления нужно учитывать, что общее сопротивление всегда будет меньше, чем сопротивление любого из включенных элементов.
Основная формула для расчета общего сопротивления при параллельном соединении нескольких резисторов выглядит следующим образом:
1/Rобщ = 1/R1 + 1/R2 + … + 1/Rn,
где Rобщ – общее сопротивление, а R1, R2, …, Rn – сопротивления отдельных резисторов. При таком подходе важно помнить, что если резистор в цепи имеет низкое сопротивление, то его вклад в общее сопротивление будет максимальным, то есть оно будет значительно уменьшаться.
Для расчета сопротивления двух резисторов в параллели можно использовать упрощенную формулу:
Rобщ = (R1 * R2) / (R1 + R2)
Этот метод позволяет быстро вычислить сопротивление для двух элементов. При большем числе резисторов расчет становится более сложным, но метод всегда остается одинаковым: сумма обратных сопротивлений всех элементов.
Основные принципы параллельного соединения резисторов
При параллельном соединении резисторов все они подключаются к одному и тому же источнику напряжения. Разница потенциалов на каждом резисторе остаётся одинаковой, в отличие от последовательного соединения, где напряжение делится. Ток, проходящий через каждый резистор, зависит от его сопротивления, и общий ток системы будет суммой токов через каждый элемент.
Общее сопротивление при параллельном соединении рассчитывается по формуле:
1 / Rобщ = 1 / R1 + 1 / R2 + … + 1 / Rn
Таким образом, общее сопротивление всегда меньше сопротивления наименьшего резистора в цепи. Это важное отличие от последовательного соединения, где общее сопротивление увеличивается.
Важно помнить, что увеличение количества резисторов в параллельном соединении снижает общее сопротивление. Например, если два резистора с сопротивлениями 6 Ом и 12 Ом подключены параллельно, общее сопротивление можно найти по формуле:
1 / Rобщ = 1 / 6 + 1 / 12 = 1 / 4
Следовательно, Rобщ = 4 Ом.
Кроме того, при параллельном соединении ток, проходящий через каждый резистор, будет зависеть от его сопротивления. Резистор с меньшим сопротивлением будет пропускать больший ток, а резистор с большим сопротивлением – меньший. Это следует учитывать при проектировании цепей с параллельным соединением, чтобы избежать перегрузки отдельных элементов.
Рекомендация: Для эффективной работы цепи важно, чтобы общее сопротивление подходило к требуемым характеристикам устройства, а также чтобы резисторы с различным сопротивлением были правильно подобраны для обеспечения безопасного и стабильного тока.
Формула расчета общего сопротивления для двух резисторов
Для расчета общего сопротивления двух резисторов, соединенных параллельно, используется следующая формула:
1/Rобщ = 1/R1 + 1/R2
Где:
- Rобщ – общее сопротивление параллельного соединения;
- R1 – сопротивление первого резистора;
- R2 – сопротивление второго резистора.
Если сопротивления резисторов одинаковы (R1 = R2), формулу можно упростить до:
Rобщ = R1 / 2
В случае, если нужно рассчитать сопротивление трех или более резисторов, аналогично добавляются новые слагаемые в правую часть уравнения:
1/Rобщ = 1/R1 + 1/R2 + 1/R3 + ...
После вычисления выражения для 1/Rобщ, результат инвертируется, чтобы получить значение общего сопротивления Rобщ:
Rобщ = 1 / (1/R1 + 1/R2 + 1/R3 + ...)
Важно помнить, что общее сопротивление параллельной схемы всегда будет меньше сопротивления любого из резисторов, участвующих в соединении. Это связано с тем, что путь для тока увеличивается, что снижает общее сопротивление.
Как использовать обратные величины при параллельном соединении
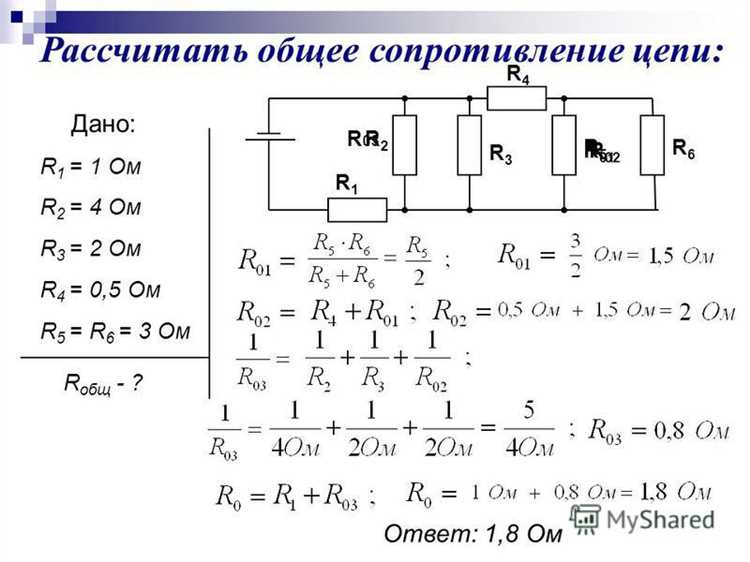
При параллельном соединении резисторов общее сопротивление рассчитывается с использованием обратных величин каждого из сопротивлений. Это связано с тем, что в параллельной схеме ток разделяется между компонентами, и их сопротивления не складываются напрямую. Вместо этого используется формула для обратных величин сопротивлений.
Для двух резисторов с сопротивлениями R1 и R2 общее сопротивление Rtotal можно вычислить по формуле:
1 / Rtotal = 1 / R1 + 1 / R2
Если резисторов больше, то формула для общего сопротивления будет выглядеть так:
1 / Rtotal = 1 / R1 + 1 / R2 + 1 / R3 + ... + 1 / Rn
После того как обратные величины всех сопротивлений сложены, необходимо найти обратную величину суммы, что и будет искомым общим сопротивлением:
Rtotal = 1 / (1 / R1 + 1 / R2 + 1 / R3 + ... + 1 / Rn)
Этот метод упрощает расчет в случае сложных схем с множеством резисторов, так как он исключает необходимость в сложении дробей с разными знаменателями. Также важно помнить, что общее сопротивление всегда будет меньше, чем наименьшее из сопротивлений в цепи.
При расчетах важно корректно учитывать единицы измерения сопротивлений, чтобы результат был получен в нужных единицах (обычно омы). При необходимости можно использовать калькуляторы или специализированные программные средства для упрощения вычислений, но важно понимать сам принцип работы с обратными величинами.
Параллельное соединение резисторов с разными значениями сопротивлений
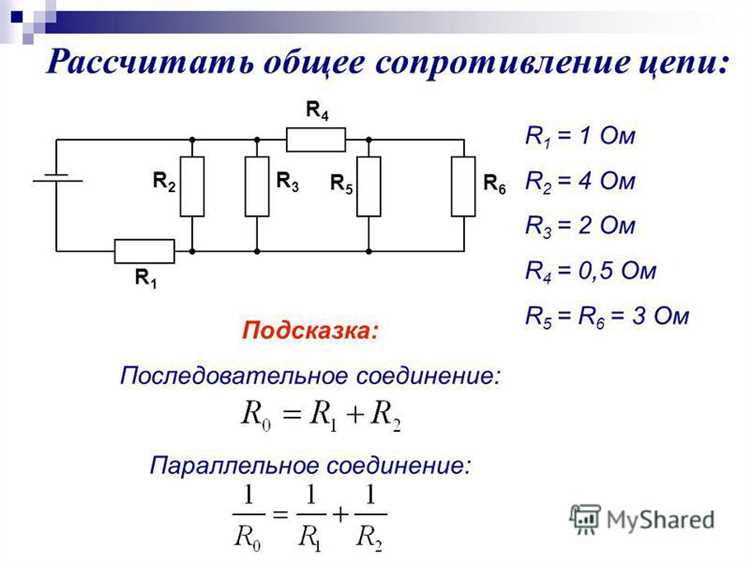
При параллельном соединении резисторов общее сопротивление рассчитывается по формуле:
1 / R_общ = 1 / R1 + 1 / R2 + 1 / R3 + ...
Где R_общ – это общее сопротивление, а R1, R2, R3 – сопротивления отдельных резисторов. Важно понимать, что при добавлении резисторов параллельно общее сопротивление уменьшается.
Чтобы наглядно объяснить это на примере, рассмотрим параллельное соединение трех резисторов:
- R1 = 10 Ом
- R2 = 20 Ом
- R3 = 30 Ом
Подставим эти значения в формулу:
1 / R_общ = 1 / 10 + 1 / 20 + 1 / 30
Вычисления дают следующее:
1 / R_общ = 0.1 + 0.05 + 0.0333 = 0.1833
Отсюда:
R_общ = 1 / 0.1833 ≈ 5.46 Ом
Таким образом, при параллельном соединении резисторов с сопротивлениями 10 Ом, 20 Ом и 30 Ом общее сопротивление составит 5.46 Ом.
Некоторые важные моменты при расчете:
- Если один из резисторов имеет низкое сопротивление (например, 1 Ом), его влияние на общее сопротивление будет доминирующим.
- При увеличении количества резисторов в параллельной цепи, общее сопротивление всегда будет меньше наименьшего сопротивления в сети.
- Параллельное соединение идеально подходит для создания цепей с необходимым ограничением тока или для уменьшения сопротивления в случаях, когда каждый резистор имеет достаточно высокое сопротивление.
Для сложных цепей с большим числом резисторов использовать подобную формулу вручную может быть неудобно. В таких случаях целесообразно воспользоваться калькуляторами или специализированными программами для быстрого расчета.
Как изменить сопротивление при добавлении дополнительных резисторов
При добавлении резисторов в параллельное соединение общее сопротивление уменьшается. Это связано с тем, что каждый новый резистор предоставляет дополнительный путь для тока. Формула для расчета общего сопротивления в параллельном соединении двух резисторов: 1/Rобщ = 1/R1 + 1/R2. При добавлении более резисторов, эта формула расширяется аналогично: 1/Rобщ = 1/R1 + 1/R2 + … + 1/Rn.
Чем меньше сопротивление отдельного резистора, тем больше влияние на общее сопротивление. Например, если в цепь добавляется резистор с низким сопротивлением, то общее сопротивление сильно снизится, поскольку дополнительный ток будет проходить через этот резистор. В то время как добавление высокоомного резистора окажет меньшее влияние на общий результат.
Для правильного расчета важно учитывать точное значение сопротивлений. Если требуется поддержание определенного общего сопротивления, нужно тщательно выбирать номиналы добавляемых резисторов. В случае, когда добавляются резисторы с одинаковым сопротивлением, общее сопротивление будет уменьшаться пропорционально количеству резисторов. Например, два резистора по 10 Ом в параллельном соединении дадут 5 Ом, а три – около 3,33 Ом.
Невозможно достичь бесконечно малого сопротивления, даже если добавлять все больше резисторов. Существует предел, который зависит от минимального сопротивления каждого отдельного элемента, что важно учитывать при проектировании схем.
Ошибки при расчете общего сопротивления и как их избежать
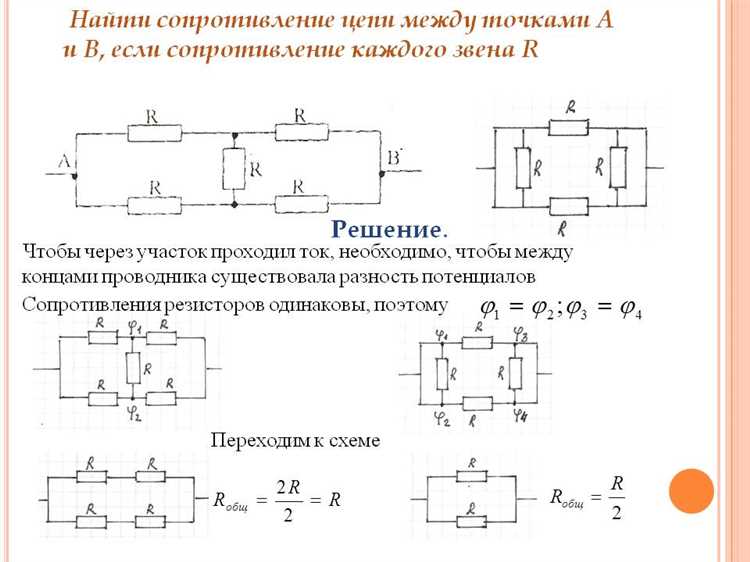
Другая распространенная ошибка – это игнорирование точности исходных данных. Если сопротивления резисторов имеют погрешности, расчет общего сопротивления без учета этих погрешностей может привести к существенным отклонениям. Для повышения точности расчетов следует учитывать допустимые погрешности каждого из элементов.
Также часто допускают ошибку при перерасчете единиц измерения. Например, если одно сопротивление задано в омах, а другое – в киломах, важно привести все сопротивления к единой единице измерения перед расчетом. Неправильная конвертация может искажать результаты.
Не следует забывать о том, что при параллельном соединении резисторы с очень большим или очень маленьким сопротивлением могут оказывать минимальное влияние на общее сопротивление. Например, если один из резисторов в параллельной цепи имеет сопротивление 10^6 Ом, его вклад в общий расчет может быть практически нулевым при наличии других резисторов с низким сопротивлением. В таких случаях можно упростить расчет, исключив несущественные элементы.
Нередко при решении задач упускают важный момент, связанный с изменениями температуры. Резисторы могут изменять свое сопротивление в зависимости от внешних условий, например, при повышении температуры. Это стоит учитывать, особенно в тех случаях, когда температура резисторов отличается от стандартных условий (20°C).
Наконец, важно помнить, что если один из резисторов в параллельном соединении имеет нулевое сопротивление (например, идеальный проводник), общее сопротивление всей цепи будет стремиться к нулю. Такой случай часто забывают учитывать, что приводит к ошибочному расчету сопротивления цепи.
Примеры практических задач для закрепления расчетов сопротивления
Задача 1: Рассчитайте общее сопротивление цепи, если в ней подключены три резистора с сопротивлениями 6 Ом, 12 Ом и 18 Ом параллельно.
Решение: Для параллельного соединения сопротивление можно вычислить по формуле: 1/R_общ = 1/R1 + 1/R2 + 1/R3. Подставим значения:
1/R_общ = 1/6 + 1/12 + 1/18 = 0,1667 + 0,0833 + 0,0556 = 0,3056.
R_общ = 1 / 0,3056 = 3,27 Ом.
Ответ: Общее сопротивление цепи составит 3,27 Ом.
Задача 2: В цепи подключены два резистора с сопротивлениями 10 Ом и 20 Ом. Рассчитайте общее сопротивление, если один из резисторов подключен в цепь параллельно другому, а затем оба резистора подключены последовательно с третьим резистором сопротивлением 15 Ом.
Решение: Сначала находим общее сопротивление первых двух резисторов, подключенных параллельно:
1/R_параллельное = 1/10 + 1/20 = 0,1 + 0,05 = 0,15.
R_параллельное = 1 / 0,15 = 6,67 Ом.
Теперь добавляем третий резистор, соединенный последовательно:
R_общ = 6,67 + 15 = 21,67 Ом.
Ответ: Общее сопротивление цепи составит 21,67 Ом.
Задача 3: В цепи из трех резисторов сопротивлениями 4 Ом, 8 Ом и 16 Ом два из них соединены параллельно, а затем результат этого соединения подключен последовательно к третьему. Рассчитайте общее сопротивление.
Решение: Сначала вычислим сопротивление параллельного соединения двух резисторов:
1/R_параллельное = 1/4 + 1/8 = 0,25 + 0,125 = 0,375.
R_параллельное = 1 / 0,375 = 2,67 Ом.
Теперь добавим сопротивление третьего резистора, подключенного последовательно:
R_общ = 2,67 + 16 = 18,67 Ом.
Ответ: Общее сопротивление цепи составит 18,67 Ом.
Задача 4: В цепи три резистора с сопротивлениями 5 Ом, 10 Ом и 15 Ом соединены параллельно. Найдите общее сопротивление.
Решение: Используем формулу для параллельного соединения:
1/R_общ = 1/5 + 1/10 + 1/15 = 0,2 + 0,1 + 0,0667 = 0,3667.
R_общ = 1 / 0,3667 = 2,73 Ом.
Ответ: Общее сопротивление цепи составит 2,73 Ом.
Задача 5: В цепи два резистора сопротивлением 3 Ом и 6 Ом соединены параллельно, а затем этот блок подключен последовательно с резистором 9 Ом. Рассчитайте общее сопротивление цепи.
Решение: Сначала вычислим сопротивление параллельного соединения:
1/R_параллельное = 1/3 + 1/6 = 0,3333 + 0,1667 = 0,5.
R_параллельное = 1 / 0,5 = 2 Ом.
Теперь добавляем сопротивление последовательно подключенного резистора:
R_общ = 2 + 9 = 11 Ом.
Ответ: Общее сопротивление цепи составит 11 Ом.
Вопрос-ответ:
Почему при параллельном соединении резисторов общее сопротивление всегда меньше минимального сопротивления из всех подключенных резисторов?
Это происходит из-за того, что параллельное соединение увеличивает путь для тока. Каждое дополнительное сопротивление в параллельной цепи дает току еще один путь, по которому он может двигаться. Таким образом, ток в цепи становится более свободным, что снижает общее сопротивление. Чем больше резисторов параллельно, тем легче электрическому току проходить через систему, и общее сопротивление уменьшается.
Как влияет добавление еще одного резистора в параллельное соединение на общее сопротивление?
Добавление нового резистора в параллельное соединение всегда уменьшает общее сопротивление. Это объясняется тем, что появляется дополнительный путь для тока, и электрический ток может протекать через новый резистор. Чем больше резисторов подключено параллельно, тем легче току двигаться, что снижает общее сопротивление цепи.