Магнитный поток через поверхность равен нулю, если вектор магнитной индукции B перпендикулярен нормали к этой поверхности или если модуль B равен нулю. Это может происходить как в результате геометрического расположения проводника, так и при отсутствии магнитного поля в области наблюдения.
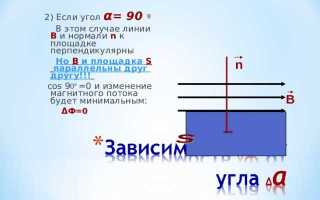
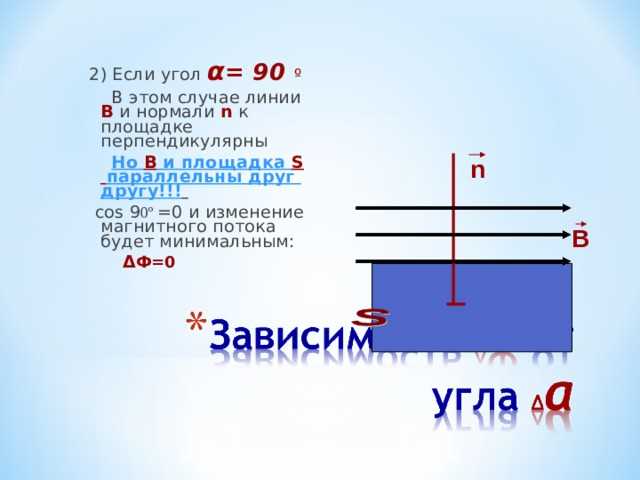
Один из типичных случаев – замкнутый контур, расположенный в плоскости, перпендикулярной направлению магнитных силовых линий. Если поле однородное и направлено параллельно плоскости контура, скалярное произведение B·S·cos(θ) даёт ноль при угле θ = 90°, что исключает появление потока.
Также магнитный поток равен нулю, если площадь поверхности, пронизанной полем, стремится к нулю. Это важно при анализе локальных изменений магнитного поля, особенно в контексте дифференциальной формы закона Фарадея. Любые искажения ориентации контура или изменение направления поля нарушают условие нулевого потока.
В приложениях, например, при проектировании катушек и датчиков Холла, соблюдение условий нулевого потока критично для снижения наводок и ложных срабатываний. Практически это реализуется за счёт симметричной компоновки элементов или экранирования от внешнего магнитного влияния.
Когда площадь контура перпендикулярна вектору магнитной индукции
Магнитный поток определяется как скалярное произведение вектора магнитной индукции B и вектора площади S: Φ = B·S·cos(θ), где θ – угол между ними. Если площадь замкнутого контура расположена строго перпендикулярно к вектору магнитной индукции, то угол θ равен 90°.
При θ = 90° значение cos(θ) становится равным нулю. Следовательно, магнитный поток через такой контур также равен нулю: Φ = B·S·cos(90°) = 0. Это ключевое условие, при котором даже при наличии магнитного поля поток не возникает.
Такое положение может быть достигнуто, например, если рамка с током или датчик размещены в магнитном поле таким образом, что их нормаль к площади лежит в плоскости силовых линий. В этом случае линии магнитной индукции проходят вдоль плоскости рамки, не «пересекают» её, и, следовательно, не создают магнитного потока.
На практике это важно при настройке катушек, датчиков Холла и измерительных систем. Например, чтобы минимизировать паразитный сигнал в катушке, её размещают так, чтобы ось витков была перпендикулярна направлению магнитного поля. Это исключает индуцирование ЭДС и снижает помехи.
Для подтверждения перпендикулярности полезно использовать векторный анализ или провести измерения с помощью чувствительных датчиков, которые фиксируют изменения при незначительном повороте. Это позволяет точно определить конфигурацию, при которой магнитный поток отсутствует.
Как изменение угла между полем и контуром влияет на поток
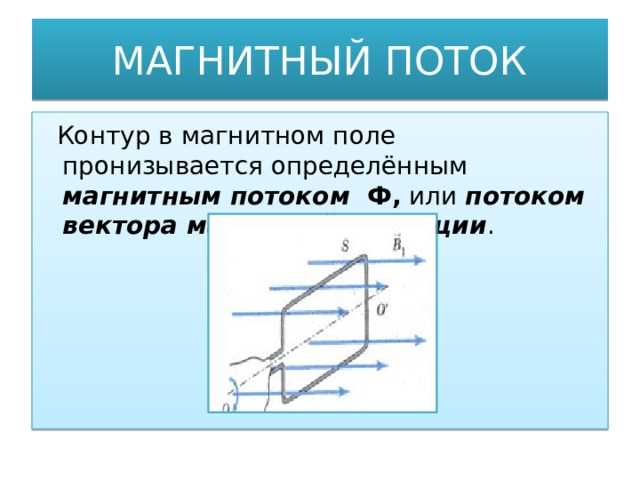
Магнитный поток через поверхность контура определяется выражением Φ = B·S·cos(θ), где B – модуль вектора магнитной индукции, S – площадь поверхности, θ – угол между вектором B и нормалью к поверхности. Именно значение угла θ напрямую влияет на величину потока.
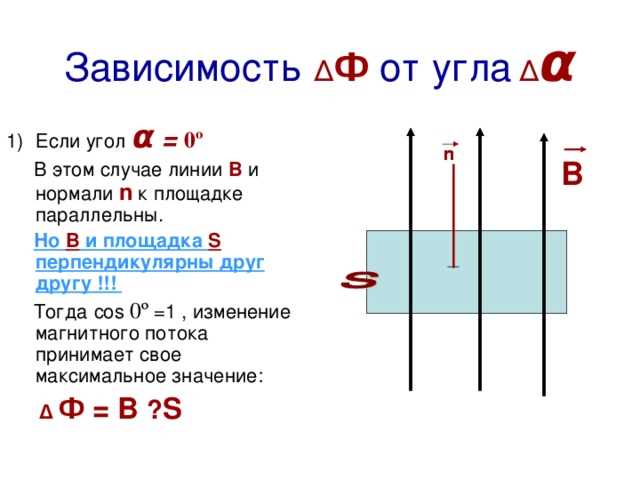
- При θ = 0° (вектор B совпадает с направлением нормали к поверхности) cos(θ) = 1, и магнитный поток достигает максимума.
- При θ = 90° (вектор B лежит в плоскости поверхности) cos(θ) = 0, поток через контур становится равным нулю.
- При θ = 180° (вектор B направлен противоположно нормали) cos(θ) = -1, поток также максимален по модулю, но с противоположным знаком.
Таким образом, малейшее изменение угла между магнитным полем и контуром приводит к изменению значения потока. Особенно важно учитывать это при расчетах, если требуется достичь условия Φ = 0. Тогда необходимо, чтобы поле располагалось строго в плоскости контура или чтобы сумма потоков от разных участков компенсировала друг друга.
Для достижения нулевого потока на практике:
- Поверните контур так, чтобы он оказался строго параллелен линиям поля.
- Используйте подвижные держатели катушек в экспериментах для точной установки угла.
- При моделировании учитывайте, что даже отклонение в 1–2 градуса может существенно повлиять на результат.
Контроль угла между вектором магнитной индукции и нормалью к площади – ключевой параметр при анализе условий равенства магнитного потока нулю.
Почему при отсутствии магнитного поля поток равен нулю
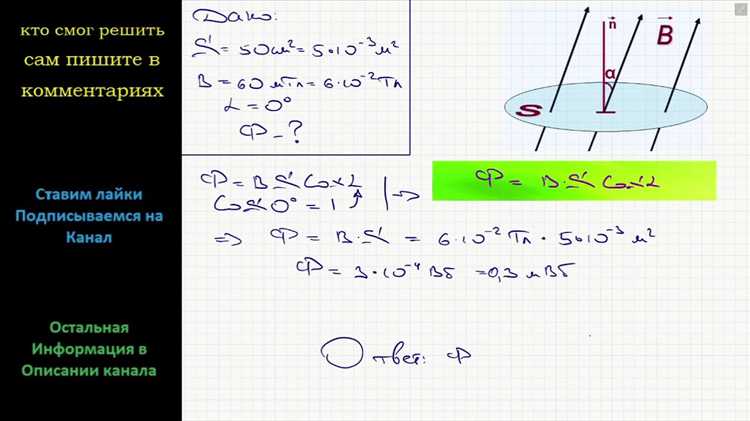
Магнитный поток определяется как скалярное произведение вектора магнитной индукции 𝐁 и вектора площади 𝐒 контура: Φ = B·S·cos(θ). При полном отсутствии магнитного поля модуль вектора 𝐁 равен нулю, то есть B = 0 Тл.
Подстановка этого значения в формулу даёт: Φ = 0·S·cos(θ) = 0. Независимо от ориентации контура и его площади, произведение с нулевым вектором магнитной индукции всегда даёт нулевой результат.
Это условие реализуется в экранированных зонах, внутри сверхпроводников в состоянии Мейснера, а также в вакууме вдали от источников магнитного поля. В этих случаях поток через любой замкнутый контур стремится к нулю, так как отсутствует сам носитель взаимодействия – магнитное поле.
Для практических измерений важно учитывать, что даже минимальное значение 𝐁 – например, от Земли (порядка 30–60 мкТл) – уже создаёт ненулевой поток. Поэтому полное отсутствие магнитного поля требует создания контролируемых лабораторных условий с экранированием внешних источников.
Что происходит при замыкании или разрыве контура
Магнитный поток определяется через интеграл по площади замкнутого контура. При этом наличие самого контура – обязательное условие. Если цепь разомкнута, площадь, ограниченная ею, считается неопределённой, и, следовательно, понятие потока теряет физический смысл.
В случае разрыва контура:
- площадь, охватываемая контуром, исчезает как замкнутая геометрическая величина;
- интеграл по поверхности становится невозможен из-за отсутствия границ;
- магнитный поток приравнивается к нулю не как результат вычислений, а по определению.
При замыкании контура:
- восстанавливается замкнутая геометрическая форма, позволяющая задать площадь интегрирования;
- если в области существует магнитное поле, то поток через контур будет отличен от нуля, при условии неперпендикулярности поля и поверхности;
- возникает возможность учитывать динамические изменения потока и, соответственно, индукцию ЭДС.
Для анализа явлений электромагнитной индукции наличие замкнутого проводящего контура – обязательное условие. Без замкнутости невозможно корректное определение ни потока, ни индуцированного напряжения.
Как геометрические параметры контура влияют на поток
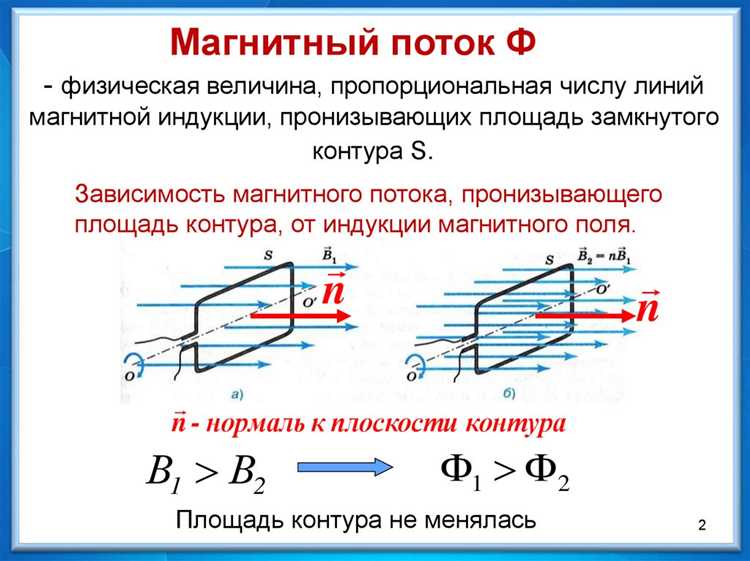
Магнитный поток определяется произведением вектора магнитной индукции на площадь проекции контура, перпендикулярную этому вектору. Следовательно, форма и размеры контура прямо влияют на величину потока.
При фиксированной величине магнитной индукции, увеличение площади контура приводит к пропорциональному увеличению потока. Например, при удвоении площади плоского прямоугольного витка в однородном поле поток удваивается.
Форма влияет на распределение потока, особенно в неравномерном поле. Круглый контур в центре симметричного поля воспринимает поток иначе, чем вытянутый эллипс при том же значении площади.
Число витков также влияет: если контур многовитковый, суммарный поток пропорционален числу витков. Один виток и катушка с десятью одинаковыми витками в одинаковых условиях дают разное значение потока – во втором случае оно в десять раз больше.
Положение и ориентация площади относительно вектора магнитной индукции также связаны с геометрией. Даже при одинаковой площади, повернутый под углом контур может давать нулевой поток, если его нормаль параллельна полю.
В каких случаях результирующий поток компенсируется
Результирующий магнитный поток компенсируется, когда суммарное значение потоков, проходящих через контур, равно нулю. Такое происходит при наложении нескольких магнитных полей, создающих потоки противоположного направления и равной величины.
Компенсация возникает, если векторные компоненты магнитной индукции, пересекающие площадь контура, ориентированы так, что положительные и отрицательные потоки взаимно уравновешивают друг друга. Например, при равенстве по модулю и противоположном направлении потоков через части контура.
Практический случай компенсации наблюдается в системах с симметрично расположенными источниками поля, где токи или магниты создают поля, которые взаимно гасят общий поток в определённых зонах.
Для достижения компенсации потока следует учитывать площадь контура, угол между вектором магнитной индукции и нормалью к поверхности, а также распределение магнитных полей вокруг контура.
Если суммарное интегральное значение магнитной индукции по поверхности контура равно нулю, результирующий поток компенсируется полностью, что подтверждается равенством
Φ = ∫ B · dS = 0,
где B – вектор магнитной индукции, dS – элемент площади с направлением нормали.
Компенсация потока может быть достигнута как стационарно (постоянные поля), так и динамически – при изменении конфигурации поля или ориентации контура относительно источников.
Когда переменное поле даёт нулевой средний поток
Средний магнитный поток через контур равен нулю, если интеграл магнитной индукции по площади контура за полный период переменного поля равен нулю. Это происходит при периодическом изменении вектора магнитной индукции с симметричной амплитудой относительно нулевого значения.
Для гармонического поля 𝑩(𝑡) = 𝑩₀·sin(ω𝑡) средний поток определяется как интеграл от B(t)·S·cos(α) по времени, где S – площадь контура, α – угол между нормалью к контуру и вектором поля. При полном периоде среднее значение sin(ω𝑡) равно нулю, следовательно, средний поток тоже равен нулю.
Если поле изменяется негармонично, условие нулевого среднего потока сохраняется при наличии равновесия положительных и отрицательных вкладов поля по времени. Несимметричные формы сигнала, постоянные сдвиги по уровню или фазовые искажения могут привести к ненулевому среднему значению потока.
Важную роль играет ориентация контура. При повороте контура так, что угол α колеблется с периодом или принимает значения, при которых косинус угла меняет знак, средний поток может стать близким к нулю независимо от амплитуды поля.
Для практического анализа рекомендуется вычислять средний поток по формуле:
| Параметр | Обозначение | Описание |
|---|---|---|
| Магнитный поток | Φ(t) | Φ(t) = B(t) · S · cos(α) |
| Средний поток | Φ_avg | Φ_avg = (1/T) ∫₀ᵀ Φ(t) dt |
| Период | T | Время полного цикла изменения поля |
| Угол между вектором и нормалью | α | Константа или функция времени |
При отсутствии постоянной составляющей и симметричном изменении поля средний поток будет равен нулю. В системах с переменным магнитным полем рекомендуется проверять наличие постоянных сдвигов, влияющих на итоговое значение.
Роль симметрии в обнулении магнитного потока

Симметрия контура и распределения магнитного поля напрямую влияет на значение магнитного потока. При наличии осевой или центральной симметрии поток через замкнутую поверхность может суммироваться к нулю за счёт компенсации вкладов противоположных участков контура.
Если магнитное поле и контур обладают зеркальной симметрией относительно плоскости, то магнитные потоки через части контура по разные стороны этой плоскости равны по модулю, но противоположны по знаку, что приводит к их взаимной компенсации.
В случае периодически изменяющихся магнитных полей с пространственной симметрией, интеграл магнитной индукции по поверхности контура может быть равен нулю из-за равенства положительных и отрицательных вкладов в разные области.
Для точного определения условий нулевого потока важно анализировать векторное распределение магнитной индукции и геометрию контура с учётом симметрий, включая поворотные и отражательные. Несоблюдение симметрии обычно приводит к ненулевому суммарному потоку.
При проектировании устройств и контуров, требующих нулевого магнитного потока, рекомендуется выбирать конфигурации с чётко выраженными симметриями, чтобы минимизировать ошибочные индуцированные токи и улучшить стабильность работы систем.
Вопрос-ответ:
При каких условиях магнитный поток через замкнутый контур становится равным нулю?
Магнитный поток равен нулю, если вектор магнитной индукции направлен перпендикулярно поверхности контура, либо если магнитные поля компенсируют друг друга так, что суммарный поток через контур исчезает. Кроме того, симметрия поля и геометрии контура может приводить к взаимному уничтожению вкладов, дающих нулевой итоговый поток.
Как влияет ориентация поверхности контура относительно вектора магнитной индукции на величину магнитного потока?
Магнитный поток рассчитывается как скалярное произведение вектора магнитной индукции на вектор площади контура. Если площадь контура повернута так, что её вектор нормали совпадает с направлением магнитного поля, поток максимален. При повороте угол между этими векторами увеличивается, и поток уменьшается, достигая нуля, когда площадь становится перпендикулярной полю.
Можно ли считать магнитный поток равным нулю, если поле внутри контура меняется во времени?
Если магнитное поле переменное, средний магнитный поток за полный период может равняться нулю, если положительные и отрицательные значения потока компенсируются. Однако в конкретный момент времени поток может быть отличен от нуля. Для устойчивого нулевого потока необходима не только временная компенсация, но и пространственное распределение поля с учетом контура.
Какая роль симметрии контура и магнитного поля в обнулении магнитного потока?
Симметричные конфигурации поля и контура часто приводят к взаимному уничтожению вкладов в магнитный поток. Например, если контур расположен так, что поле с одной стороны создает поток, равный по модулю и противоположный по знаку потоку с другой стороны, общий поток становится равен нулю. Это часто используется в практических задачах для снижения влияния внешних магнитных полей.
Почему при отсутствии магнитного поля магнитный поток через контур всегда равен нулю?
Магнитный поток определяется интегралом магнитной индукции по поверхности контура. Если магнитное поле отсутствует, вектор магнитной индукции равен нулю во всех точках поверхности, и интеграл соответственно равен нулю. Таким образом, без поля поток не может иметь ненулевого значения.