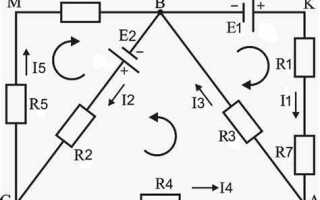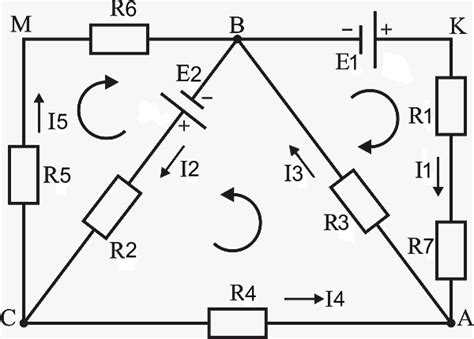
Второй закон Кирхгофа позволяет составлять уравнения для замкнутых контуров электрических цепей, отражающих баланс напряжений. Число таких уравнений не произвольно: оно зависит от топологии схемы, в частности от количества независимых контуров. Именно эти уравнения необходимы для полной математической модели цепи при расчёте токов и напряжений методом контурных токов.
Для плоской схемы с b ветвями и n узлами количество независимых уравнений по второму закону Кирхгофа определяется как k = b — (n — 1). Это значение соответствует числу фундаментальных (независимых) контуров, каждый из которых позволяет составить одно уравнение. Все остальные уравнения, записанные по другим контурам, будут линейно зависимыми от этих базовых.
При анализе сложных цепей важно правильно выбрать контуры, чтобы исключить избыточность уравнений. Использование избыточных уравнений приводит к громоздкой системе с излишними переменными, а иногда – к противоречиям при наличии ошибок. Поэтому при практическом решении задач применяют топологический подход с построением графа цепи и выделением дерева и фундаментальных контуров.
Для ускорения расчётов в символьной или численной форме рекомендуется заранее определить минимальное число необходимых уравнений и соответствующим образом оптимизировать порядок их записи. Это особенно критично в схемах с большим числом элементов, где каждый лишний контур увеличивает вычислительную нагрузку и сложность анализа.
Как определить количество независимых контуров в электрической схеме
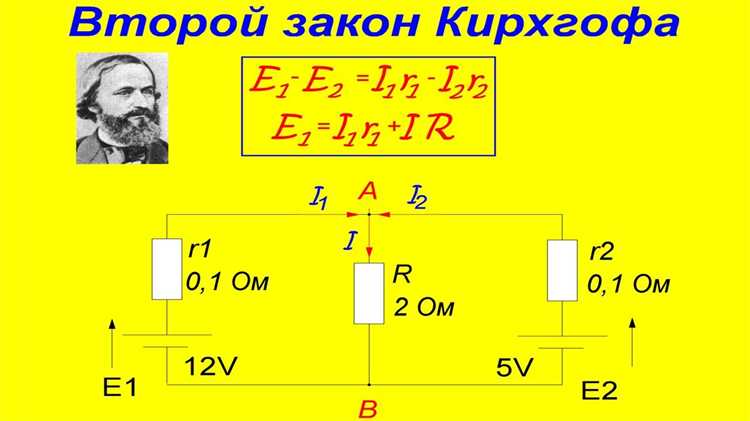
Количество независимых контуров в электрической цепи определяется с помощью топологических свойств схемы и рассчитывается по формуле:
L = R — N + 1,
где L – число независимых контуров, R – число ветвей, N – число узлов в схеме. Эта формула применяется к связной схеме, в которой все элементы соединены электрически.
Чтобы определить параметры для формулы, необходимо последовательно выполнить следующие действия:
1. Подсчитать общее количество ветвей – это все отрезки цепи, включающие элементы, соединённые между двумя узлами (например, резисторы, источники, конденсаторы).
2. Определить число узлов – это точки соединения трёх и более ветвей. Каждый уникальный узел учитывается один раз.
3. Убедиться, что схема связная. Если есть изолированные фрагменты, для каждого из них формула применяется отдельно, а затем результаты суммируются.
Количество независимых контуров соответствует числу уравнений, которые можно записать по второму закону Кирхгофа. Каждый контур должен содержать хотя бы одну ветвь, не входящую в другие независимые контуры. Это условие исключает линейную зависимость между уравнениями и обеспечивает корректность расчётов.
Для сложных схем рекомендуется использовать методы графической топологии, например, построение остовного дерева схемы. Независимые контуры определяются добавлением к остовному дереву тех ветвей, которые формируют замкнутые петли – именно они и дают нужное количество уравнений по второму закону Кирхгофа.
Что влияет на количество уравнений по второму закону Кирхгофа
Количество уравнений по второму закону Кирхгофа напрямую зависит от количества независимых контуров в электрической схеме. Под независимыми контурами понимаются такие замкнутые пути, для которых нельзя получить уравнение, складывая другие уравнения контуров схемы. Их число определяет, сколько уникальных уравнений можно составить на основе закона напряжений.
Основной параметр, влияющий на число независимых контуров, – это топология схемы. В расчетах используется формула: k = l — n + 1, где k – число независимых контуров, l – количество ветвей, n – количество узлов. Эта формула применима к связной схеме без изолированных фрагментов.
Число ветвей определяется количеством участков цепи с единственным путем прохождения тока, а узлы – точками соединения трех и более проводников. Если схема содержит источники ЭДС в разных ветвях, их расположение также влияет на необходимость введения дополнительных уравнений для учета всех напряжений.
Дополнительные элементы, такие как диоды, трансформаторы, зависимые источники и операционные усилители, могут изменить структуру контура и потребовать пересмотра количества уравнений. В цепях с мостовыми соединениями или с параллельными ветвями важно учитывать возможное дублирование уравнений при неправильном выборе контуров.
Правильный выбор базиса контуров позволяет избежать линейно зависимых уравнений и оптимизировать систему для дальнейшего расчета токов и напряжений. Применение метода циклов или матричных методов (например, инцидентных и контурных матриц) упрощает определение необходимого количества уравнений при анализе сложных схем.
Связь между числом ветвей, узлов и контуров
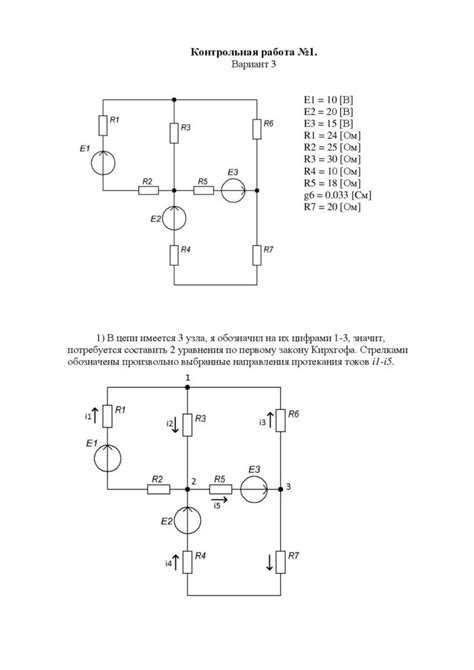
В анализе электрических цепей важную роль играет взаимосвязь между числом ветвей (B), узлов (N) и независимых контуров (L). Эта связь формализуется через топологическую формулу: L = B — N + 1. Она позволяет точно определить количество уравнений по второму закону Кирхгофа, необходимых для описания замкнутых токовых контуров в схеме.
Каждая ветвь – это участок цепи с единственным током, каждая точка соединения трёх и более ветвей считается узлом, а независимые контуры – это минимальное количество замкнутых путей, через которые можно выразить все возможные токи в цепи.
Для практического применения: если в цепи 10 ветвей и 5 узлов, то число независимых контуров составляет L = 10 — 5 + 1 = 6. Следовательно, необходимо составить 6 уравнений по второму закону Кирхгофа, чтобы получить полное описание токов по контурам.
При построении уравнений следует учитывать только независимые контуры, так как остальные можно выразить через комбинацию уже выбранных. Избыточные уравнения приведут к линейной зависимости и не повысят точность анализа.
Таким образом, правильное определение количества ветвей и узлов – обязательный шаг для корректного составления системы уравнений и дальнейшего расчета токов и напряжений в сложных электрических цепях.
Как построить уравнения для замкнутых контуров

Для построения уравнений по второму закону Кирхгофа необходимо выбрать независимые замкнутые контуры, охватывающие все элементы схемы. Количество таких контуров рассчитывается по формуле: k = b — n + 1, где k – число независимых контуров, b – число ветвей, n – число узлов.
Каждое уравнение составляется на основе правила: сумма падений напряжений и ЭДС по замкнутому контуру равна нулю. Следует зафиксировать направление обхода (по часовой стрелке или против), придерживаться его во всех расчетах и согласовать полярности всех ЭДС и направлений токов.
При прохождении через резистор знак напряжения определяется направлением обхода относительно тока: если обход идет по направлению тока, напряжение считается со знаком минус; в противном – со знаком плюс. Для ЭДС знак зависит от направления обхода относительно полярности источника: обход от минуса к плюсу – плюс, от плюса к минусу – минус.
В каждом уравнении должны быть учтены все элементы, входящие в контур, включая резисторы, источники ЭДС и, при наличии, другие пассивные и активные компоненты. Коэффициенты при токах определяются сопротивлениями, а слагаемые с ЭДС – по указанным правилам знаков.
После составления системы уравнений производится их алгебраическое упрощение и дальнейшее решение – обычно методом подстановки, Гаусса или через матрицы. Корректность системы проверяется сопоставлением количества уравнений с числом неизвестных токов.
Примеры расчёта числа уравнений для типовых схем
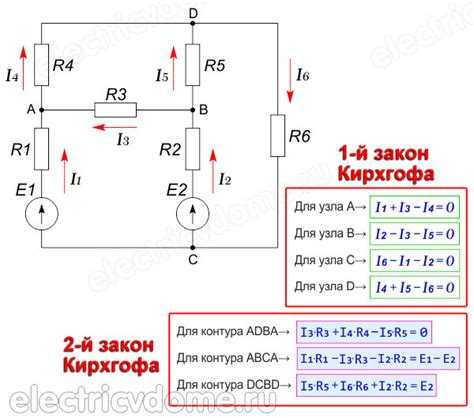
Для анализа электрических цепей по второму закону Кирхгофа важно уметь определять количество независимых уравнений. Это количество соответствует числу независимых замкнутых контуров, которое можно вычислить по формуле:
L = B — N + 1,
где:
- L – число независимых контуров (и, соответственно, уравнений по второму закону Кирхгофа);
- B – число ветвей;
- N – число узлов.
Ниже приведены конкретные примеры расчётов для разных типов схем.
Пример 1. Треугольник из трёх резисторов
- Ветви: 3
- Узлы: 3
- L = 3 — 3 + 1 = 1
В этой схеме возможен только один независимый контур, и, соответственно, одно уравнение по второму закону Кирхгофа.
Пример 2. Замкнутый четырёхугольник с диагональю
- Ветви: 5 (четыре стороны и одна диагональ)
- Узлы: 4
- L = 5 — 4 + 1 = 2
В этой схеме два независимых контура: один по трём сторонам, другой по двум сторонам и диагонали.
Пример 3. Две ячейки, соединённые последовательно
- Ветви: 7
- Узлы: 4
- L = 7 — 4 + 1 = 4
Для такой схемы необходимо составить четыре независимых уравнения по второму закону Кирхгофа – по числу минимальных замкнутых контуров, не выражаемых друг через друга.
Пример 4. Полный граф с четырьмя узлами
- Ветви: 6 (все возможные соединения между четырьмя узлами)
- Узлы: 4
- L = 6 — 4 + 1 = 3
Три уравнения описывают независимые петли, каждая из которых включает отдельное соединение между узлами.
Для сложных схем важно не только формально применять формулу, но и уметь выделять именно независимые контуры. Избыточные уравнения не увеличивают точность анализа, но могут привести к линейной зависимости в системе.
Когда возникает линейная зависимость между уравнениями
- Если сумма напряжений по одному замкнутому контуру может быть выражена через сумму напряжений по другим контурам, уравнения оказываются неявно связаны.
- При избыточном числе контуров, превышающем количество независимых циклов схемы, уравнения повторяют друг друга или сводятся к линейной комбинации других.
- Наличие мостовых или параллельных ветвей, которые создают дополнительные контуры без увеличения независимых циклов.
- Использование контуров, содержащих общие ветви с другими контурами, при неправильном выборе базиса контуров.
Рекомендации для предотвращения линейной зависимости уравнений:
- Определять количество независимых контуров по формуле: Число независимых контуров = Число ветвей − Число узлов + 1.
- Выбирать базис контуров с учётом минимального пересечения ветвей между ними.
- Избегать повторного использования контуров, являющихся линейными комбинациями уже выбранных.
- Проверять уравнения на линейную зависимость с помощью алгебраических методов, например, с помощью ранга матрицы коэффициентов.
Игнорирование этих правил приводит к избыточности системы уравнений и усложняет её решение, снижая эффективность расчёта электрических цепей.
Можно ли сократить количество уравнений без потери точности
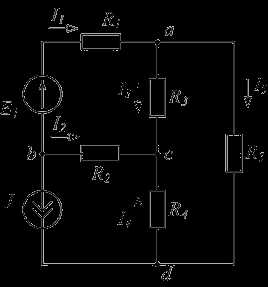
Количество уравнений по второму закону Кирхгофа определяется числом независимых контуров в электрической схеме, что равно разности числа ветвей и узлов плюс один (m — n + 1). Попытка сократить число уравнений ниже этого значения ведёт к потере полноты системы и неточности решения.
Однако в ряде случаев возможно исключение из рассмотрения контуров, линейно зависимых от других, без влияния на точность расчёта. Для этого проводится анализ линейной зависимости уравнений. Если одно уравнение может быть выражено через сумму других, его исключают, сохраняя только базовый набор независимых уравнений.
Практический метод сокращения – построение минимального набора независимых контуров с помощью графовых алгоритмов (например, поиск остовного дерева). Это исключает избыточные уравнения и сохраняет полноту модели.
При сложных схемах с большим числом ветвей и узлов численное решение уравнений зачастую оптимизируют за счёт предварительного упрощения схемы: замена параллельных или последовательных элементов эквивалентными, что уменьшает количество контуров и, соответственно, уравнений.
Итог: сокращение количества уравнений возможно только путём удаления линейно зависимых или эквивалентных контуров, при этом количество независимых уравнений остаётся неизменным, что гарантирует сохранение точности расчетов.
Ошибки при составлении уравнений и как их избежать
Частая ошибка – выбор контуров с линейно зависимыми уравнениями. Это приводит к избыточности и усложнению решения. Чтобы избежать, необходимо внимательно проверять, что каждый контур добавляет уникальное уравнение. Используйте метод определения независимых контуров, исходя из формулы число контуров = число ветвей — число узлов + 1.
Неправильное направление обхода контура или полярности напряжений ведёт к знаковым ошибкам. Рекомендуется строго придерживаться единого направления обхода (обычно – по часовой стрелке) и фиксировать полярность каждого источника и падения напряжения на элементах. Используйте схему с проставленными знаками для контроля.
Игнорирование источников ЭДС или внутренних сопротивлений приводит к неполным уравнениям. Каждый источник в контуре должен учитываться с учётом своего внутреннего сопротивления и знака ЭДС. Отсутствие этого шага снижает точность расчетов и нарушает баланс напряжений.
Ошибка при записи суммирования напряжений – пропуск знаков минус или плюс у падений напряжений на элементах. Для предотвращения этой ошибки рекомендуется вести уравнения с чёткой фиксацией направления тока и напряжений, используя обозначения и схемы, а затем сверять с правилами Кирхгофа.
Составление уравнений без предварительного анализа схемы часто приводит к неправильному выбору контуров и ветвей. Обязательно выполняйте предварительный разбор схемы на узлы и ветви, фиксируйте токи и направления, чтобы обеспечить корректность формулировок.
Применение стандартных шаблонов без учета особенностей конкретной схемы вызывает ошибки. Каждая схема уникальна, поэтому уравнения по второму закону Кирхгофа нужно формулировать с учётом специфики компонентов и связей между ними.
Использование автоматических инструментов для составления уравнений без проверки корректности приводит к ошибкам. Всегда перепроверяйте результаты, используя баланс узлов и контрольные вычисления, чтобы избежать накопления системных ошибок.
Вопрос-ответ:
Как определяется количество уравнений по второму закону Кирхгофа для электрической цепи?
Количество уравнений, записываемых по второму закону Кирхгофа, равно числу независимых замкнутых контуров в электрической схеме. Этот параметр вычисляется как разность между числом ветвей и числом узлов, увеличенной на единицу: количество контуров = число ветвей — число узлов + 1. Каждое уравнение отражает баланс напряжений по одному из таких контуров.
Почему нельзя записывать уравнения по второму закону Кирхгофа для всех возможных контуров одновременно?
Если составить уравнения для всех контуров, часть из них будет линейно зависимой и не даст новой информации. Избыточные уравнения приводят к избыточности и усложнению расчетов без увеличения точности. Поэтому выбирают только набор независимых контуров, обеспечивающий минимальное количество уравнений, необходимых для решения схемы.
Какая связь между количеством уравнений по второму закону Кирхгофа и структурой электрической схемы?
Структура схемы определяет число ветвей и узлов, а значит, и количество независимых контуров. Сложные схемы с большим числом ветвей обычно имеют больше контуров, а значит, и больше уравнений по второму закону Кирхгофа. Изменение структуры — например, добавление ветвей или узлов — влияет на количество уравнений, что отражает закономерности топологии схемы.
Как избежать ошибок при составлении уравнений по второму закону Кирхгофа?
Внимательно выбирайте независимые контуры, чтобы исключить линейную зависимость уравнений. Правильно определяйте направление обхода контуров и учитывайте знаки напряжений. Проверяйте корректность подключения элементов и напряжений, особенно источников. Важно сверять итоговые уравнения с топологией схемы и логикой её работы.
Можно ли уменьшить количество уравнений, не потеряв точность расчёта по второму закону Кирхгофа?
Да. Уменьшение количества уравнений достигается за счёт выбора минимального набора независимых контуров. Это не снижает точность, так как зависимые уравнения не добавляют новую информацию. Такой подход упрощает решение системы и ускоряет вычисления, сохраняя полную достоверность результатов.