Кривизна параболического зеркала – это важный параметр, который определяет его фокусные свойства и позволяет точно моделировать его геометрию. В физике и инженерии для описания кривизны часто используется несколько единиц измерения, каждая из которых имеет свои особенности и области применения. Одной из наиболее распространенных единиц является радиус кривизны, который характеризует степень изгиба поверхности зеркала. Радиус кривизны можно рассматривать как радиус сферы, на которой можно вписать данное зеркало.
Другой важной единицей является параметр кривизны, который определяется как обратная величина радиуса кривизны. Параметр кривизны дает возможность более компактно представлять информацию о геометрии зеркала и часто используется в теоретических расчетах. Для параболического зеркала этот параметр напрямую связан с фокусным расстоянием и может быть использован для определения фокусной кривизны, что является важным аспектом при проектировании оптических систем.
При проектировании оптических приборов, например, телескопов или лазерных систем, также может использоваться сфера кривизны, которая представляет собой сферу с радиусом, равным расстоянию от фокуса до зеркала. Эта величина позволяет точно контролировать дефекты формы и минимизировать аберрации, что особенно важно при работе с высокоточными оптическими инструментами.
Таким образом, выбор единицы измерения кривизны параболического зеркала зависит от целей проектирования и конкретных требований к точности и характеристикам отражающей поверхности. Правильный выбор и использование этих единиц обеспечивают надежность и эффективность работы оптических систем, минимизируя влияние искажений на качество изображения.
Что такое радиус кривизны и как его измерить для параболического зеркала?

Чтобы измерить радиус кривизны параболического зеркала, важно учитывать, что парабола, по сути, является аппроксимацией части сферы. Основное отличие состоит в том, что радиус кривизны для параболического зеркала зависит от его фокусного расстояния. Для параболы с фокусом в точке F, радиус кривизны можно найти, используя формулу, связывающую фокусное расстояние с радиусом кривизны:
R = 2f, где R – радиус кривизны, а f – фокусное расстояние параболы.
Таким образом, для параболического зеркала радиус кривизны всегда будет в два раза больше фокусного расстояния. Для практического измерения можно использовать метод, при котором измеряется фокусное расстояние зеркала. Для этого необходимо найти фокус и измерить расстояние от фокуса до поверхности зеркала. Эта величина и будет являться фокусным расстоянием, после чего по формуле можно рассчитать радиус кривизны.
Также можно использовать оптические приборы, такие как коллиматор, для более точного определения фокуса. Измерив точку фокуса и учитывая полученное значение, можно точно вычислить радиус кривизны зеркала, что важно для точности оптических систем.
Как использовать фокусное расстояние для расчёта кривизны параболического зеркала?
Для определения кривизны параболического зеркала важно понимать связь между его фокусным расстоянием и радиусом кривизны. Параболическое зеркало имеет форму параболы, и его кривизна зависит от того, как быстро меняется угловая поверхность, с которой световые лучи отражаются к фокусной точке. Радиус кривизны зеркала, в свою очередь, можно рассчитать, исходя из фокусного расстояния.
Формула для расчёта радиуса кривизны (R) параболического зеркала напрямую связана с фокусным расстоянием (f) и выглядит следующим образом:
R = 2f
Эта формула предполагает, что фокусное расстояние является половиной радиуса кривизны. Это свойство параболического зеркала объясняется геометрией параболы, где фокусная точка лежит на оси симметрии, а радиус кривизны равен расстоянию от фокуса до поверхности зеркала в любой его точке.
Зная фокусное расстояние, можно с высокой точностью определить кривизну зеркала. Например, если фокусное расстояние зеркала составляет 50 см, то радиус кривизны будет равен 100 см. Таким образом, для создания зеркала с конкретной кривизной достаточно контролировать его фокусное расстояние при производстве.
Этот метод широко используется в производстве и настройке параболических зеркал, применяемых в астрономии, оптике и других областях, где критична высокая точность фокусировки света. Понимание взаимосвязи между фокусным расстоянием и кривизной позволяет достигать нужных параметров зеркала, не прибегая к сложным расчетам или экспериментам.
Измерение кривизны параболы с помощью метода осевого отражения
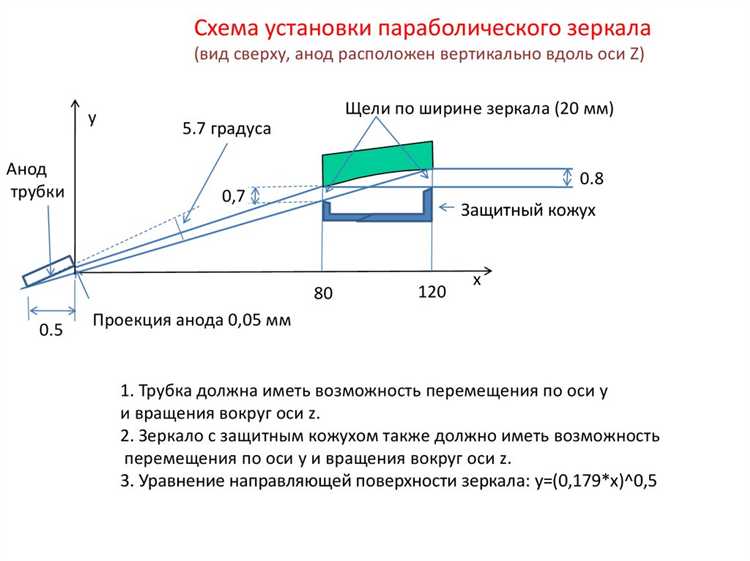
Метод осевого отражения используется для точного определения кривизны параболического зеркала. Этот метод основывается на принципе отражения света, где параболическая форма зеркала гарантирует, что все лучи, параллельные оси симметрии, будут отражаться в фокус. Для измерения кривизны важно установить несколько параметров: фокусное расстояние, положение фокуса и диаметр зеркала.
Шаг 1: Подготовка зеркала
Перед проведением измерений необходимо убедиться, что параболическое зеркало очищено от загрязнений, а его поверхность ровная. Установка зеркала должна быть строго вертикальной, а его ось симметрии – соосной с осью измерений. Параллельные лучи света можно получить с помощью лазера или специально настроенного источника света.
Шаг 2: Направление параллельных лучей
Луч света должен быть направлен параллельно оси симметрии зеркала. Для этого используется лазер или другие точечные источники, которые обеспечивают равномерное распределение лучей по оси. Лучи, направленные под углом к оси симметрии, могут привести к искажению данных.
Шаг 3: Регистрация отражённых лучей
После отражения лучей от поверхности зеркала они должны быть сфокусированы в одну точку. Местоположение фокуса зависит от кривизны зеркала и её точности. Для определения фокуса используют экраны или датчики, которые могут фиксировать точку пересечения лучей. Это значение непосредственно связано с фокусным расстоянием зеркала.
Шаг 4: Расчёт кривизны
Кривизна параболы определяется через фокусное расстояние. Измерив расстояние от фокуса до зеркала (точки, где пересекаются отражённые лучи), можно вычислить радиус кривизны. В идеальном случае радиус кривизны равен половине фокусного расстояния. Однако на практике может потребоваться корректировка в зависимости от точности установки и оборудования.
Шаг 5: Анализ результатов
Для подтверждения правильности измерений рекомендуется провести серию повторных замеров с использованием различных источников света и углов наклона. Несоответствия в данных могут указывать на дефекты зеркала или ошибки в настройке измерительной системы.
Как взаимосвязаны параметры кривизны и точность фокусировки?

Кривизна параболического зеркала напрямую влияет на его способность фокусировать свет, что важно для большинства оптических систем, включая телескопы и камеры. Параметры кривизны зеркала, такие как радиус кривизны и фокусное расстояние, определяют, насколько точно система может сфокусировать свет в одной точке – фокусе.
Радиус кривизны зеркала – это расстояние от вершины параболы до её фокуса. Чем меньше этот радиус, тем сильнее кривизна зеркала, и, следовательно, тем меньше фокусное расстояние. При этом чем меньше фокусное расстояние, тем более чувствительна система к погрешностям в точности формы зеркала. Небольшие отклонения от идеальной параболической формы приводят к значительному ухудшению фокусировки, так как лучи света могут не сходиться в одной точке, а создавать рассеянное пятно.
Точность фокусировки, в свою очередь, зависит от того, насколько близко отражённые лучи сходятся в фокусе. Если форма зеркала отклоняется от идеальной параболы, например, из-за дефектов в процессе производства или механических повреждений, это приводит к аберрациям, которые ухудшают чёткость изображения. Особенно критична такая погрешность для зеркал с небольшим фокусным расстоянием, где даже минимальные отклонения существенно снижают точность фокусировки.
Для достижения высокой точности фокусировки важно учитывать не только геометрические параметры зеркала, но и качество его поверхности. Для этого проводят высокоточную обработку и шлифовку зеркал, а также используют специальные методы контроля, такие как интерферометрия, для выявления микроскопических отклонений.
При проектировании зеркала для определённой задачи необходимо учитывать баланс между кривизной и необходимой точностью фокусировки. Чем больше кривизна, тем выше требования к точности изготовления, и наоборот. Например, для использования в астрономических телескопах требуются зеркала с минимальными отклонениями от идеальной формы, что обеспечивает резкость и чёткость изображения далёких объектов.
Практическое использование единиц измерения кривизны в оптических системах
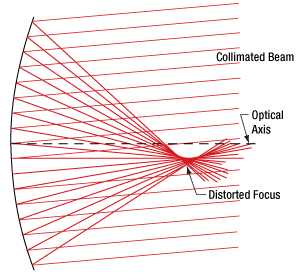
В практическом применении эти единицы измеряются и используются следующим образом:
- Радиус кривизны (R) – основной параметр, определяющий степень кривизны зеркала. Чем меньше радиус, тем сильнее кривизна, что влияет на фокусировку световых лучей. Радиус кривизны связан с фокусным расстоянием (f) через соотношение: f = R/2.
- Фокусное расстояние (f) является главным параметром при проектировании оптических систем с параболическими зеркалами. Оно определяет, на каком расстоянии от зеркала фокусируются лучи. Для точных измерений фокусное расстояние должно быть оптимизировано с учетом расстояния до объекта и требуемой разрешающей способности.
При проектировании телескопов или зеркальных микроскопов, где параболические зеркала используются для фокусировки света, правильный расчет кривизны позволяет достичь минимальных аберраций и максимальной четкости изображения. В таких системах крайне важно учитывать отклонения, вызванные неправильной кривизной зеркала, так как они могут привести к потерям резкости и искажению изображения.
Также кривизна зеркала влияет на фокусировку в системах с переменной фокусировкой, таких как камеры. Здесь правильный расчет радиуса кривизны необходим для точной настройки резкости на различных дистанциях.
- Оптимизация кривизны для камеры требует анализа условий съемки, таких как освещенность и удаленность объекта, для обеспечения идеальной фокусировки и минимизации хроматических аберраций.
- Кривизна поверхности параболического зеркала должна быть точной на уровне микрон для применения в высокоточных оптических системах, таких как спутниковые антенны и лазерные установки.
Для достижения наилучших оптических характеристик важно проводить калибровку и проверку геометрии зеркала в процессе его производства и эксплуатации. Даже незначительные отклонения от идеальной кривизны могут существенно повлиять на производительность системы.
Как поправки на материал зеркала влияют на расчёты кривизны?
При расчётах кривизны параболического зеркала важно учитывать физические свойства материала, из которого оно изготовлено. Параметры, такие как коэффициент термического расширения, механические свойства, а также оптические характеристики, напрямую влияют на форму зеркала в реальных условиях эксплуатации.
Материалы, из которых делают зеркала, имеют различные температурные коэффициенты расширения. Это означает, что при изменении температуры зеркало будет изменять свою форму, что, в свою очередь, влияет на его кривизну. Например, алюминий, обладая высоким коэффициентом расширения, при нагревании может существенно деформироваться, что повлияет на точность отражения. Это необходимо учитывать при проектировании зеркал для высокоточных оптических систем, например, в телескопах или лазерных установках.
Для компенсации этих деформаций в расчетах кривизны часто вводятся поправки на температурные изменения. Одним из решений является использование материалов с низким коэффициентом термического расширения, таких как кварц или стекло с добавками. Важно, что при использовании таких материалов поправки на тепловое расширение будут минимальными, что повышает стабильность отражающих свойств зеркала.
Ключевым аспектом также является механическая прочность материала. Зеркала, изготовленные из хрупких материалов, могут подвергаться микротрещинам при высоких механических нагрузках, что изменяет их кривизну и приводит к искажению изображений. Для таких зеркал необходимо учитывать влияние микротрещин и других дефектов на расчёты кривизны, а также применять подходы к усилению конструкции, чтобы предотвратить деформацию при воздействии внешних сил.
Оптические характеристики материала также играют свою роль. Например, в зеркалах для инфракрасных наблюдений важно, чтобы коэффициент отражения был стабильным на всех длинах волн, а материал не менял свои оптические свойства в зависимости от температуры или влажности. В таких случаях важно корректировать расчёты кривизны с учётом изменения оптических свойств зеркала при различных внешних условиях.
Итак, для точных расчётов кривизны параболического зеркала необходима интеграция поправок на температурные и механические изменения, а также точный учет оптических характеристик материала. Это позволяет минимизировать ошибки и обеспечить требуемое качество отражения.
Вопрос-ответ:
Что такое единица измерения кривизны параболического зеркала?
Единицей измерения кривизны параболического зеркала является радиус кривизны, который определяется как расстояние от фокуса зеркала до его вершины. Это значение напрямую связано с фокусным расстоянием зеркала и используется для оценки его геометрических свойств.
Как радиус кривизны влияет на фокусное расстояние параболического зеркала?
Радиус кривизны зеркала и его фокусное расстояние взаимосвязаны. Чем больше радиус кривизны, тем длиннее фокусное расстояние. Для параболического зеркала, фокусное расстояние равно половине радиуса кривизны, что означает, что изменение радиуса сразу меняет фокусное расстояние.
Как рассчитывается кривизна параболического зеркала?
Кривизна параболического зеркала рассчитывается как обратная величина радиуса кривизны. Это выражается формулой \( \kappa = \frac{1}{R} \), где \( \kappa \) — кривизна, а \( R \) — радиус кривизны. Для параболического зеркала эта величина играет ключевую роль в формировании его фокусирующих свойств.
Может ли кривизна параболического зеркала быть отрицательной?
Кривизна параболического зеркала обычно считается положительной, если зеркало выпуклое (то есть отражает свет от фокуса наружу). Однако, в некоторых контекстах, например, для гиперболического зеркала, кривизна может быть отрицательной, что означает иную форму зеркала, но для параболического зеркала этот параметр всегда положителен.
Зачем важно учитывать кривизну при проектировании параболического зеркала?
При проектировании параболического зеркала важно точно учитывать его кривизну, поскольку она влияет на точность фокусировки света. Если кривизна не соответствует требуемым параметрам, зеркало может не собирать свет в нужной точке, что снизит его эффективность. Это особенно важно в астрономии и оптике, где даже малые погрешности могут существенно повлиять на результаты наблюдений.






