Буква y в электротехнике чаще всего используется для обозначения проводимости (англ. admittance) – величины, обратной электрическому сопротивлению. Проводимость измеряется в сименсах (См) и рассчитывается по формуле y = 1 / Z, где Z – полное сопротивление цепи. Это обозначение особенно важно при анализе переменных токов, в которых сопротивление носит комплексный характер.
Комплексная проводимость y включает два компонента: активную проводимость (g) и реактивную (susceptance, b), выражается как y = g + jb. Здесь g – проводимость, обусловленная реальными потерями в цепи, а b – мера реактивных свойств, связанных с индуктивностями и ёмкостями. Такая запись упрощает расчёты в цепях переменного тока, особенно при использовании матриц проводимости в методах узлового анализа.
Применение обозначения y критично в схемотехнике, при проектировании усилителей, фильтров и систем передачи сигналов. Например, при анализе ВЧ-цепей используется параметр y в составе y-параметров, где каждая из четырёх составляющих матрицы описывает взаимосвязи токов и напряжений на входах и выходах двухполюсника. Это позволяет моделировать поведение сложных электронных компонентов и узлов с высокой точностью.
При расчётах важно учитывать частотную зависимость y: для идеального конденсатора y = jωC, а для катушки – y = 1 / (jωL). Эти выражения позволяют напрямую включать элементы в уравнения цепи, минуя промежуточные преобразования. Такая формализация существенно упрощает автоматизированное моделирование и повышает точность анализа высокочастотных и импульсных схем.
Что обозначает переменная y в уравнениях цепей переменного тока

Проводимость выражается в сименсах (См) и состоит из действительной части – проводимости g и мнимой части – сусцептанса b: y = g + jb, где j – мнимая единица.
Использование переменной y оправдано в задачах анализа параллельных цепей, где расчет токов и напряжений упрощается при переходе от импедансов к проводимостям. Например, для двух параллельных ветвей с проводимостями y₁ и y₂, эквивалентная проводимость цепи определяется как yэкв = y₁ + y₂.
В уравнениях переменного тока y применяется в комплексной форме, особенно при использовании метода узлового анализа. При этом уравнения токов записываются в виде:
I = Y·V
где I – вектор токов в узлах, V – вектор узловых напряжений, Y – матрица проводимостей, элементы которой содержат значения y между узлами цепи.
Для пассивных элементов значения y определяются так:
- Резистор: y = 1/R
- Конденсатор: y = jωC
- Катушка индуктивности: y = 1/(jωL)
Корректное использование y позволяет повысить точность расчетов, упростить численные процедуры в компьютерном моделировании и избежать ошибок при работе с параллельными структурами в частотной области.
Использование y для описания проводимости в комплексной форме
В электротехнике обозначение y применяется для представления комплексной проводимости – аналогичной импедансу величины, но в форме, удобной для параллельных схем. Комплексная проводимость определяется как обратная к комплексному импедансу: y = 1/z, где z – комплексное сопротивление цепи.
Проводимость y выражается в символической форме: y = g + jb, где g – активная (реальная) проводимость, b – susceptance, мнимая часть, характеризующая реактивную составляющую. Измеряются обе составляющие в сименсах (S). При этом знак b зависит от характера реактивного элемента: для индуктивности b < 0, для ёмкости – b > 0.
Для расчётов в высокочастотной технике и СВЧ-цепях представление через y удобно, так как позволяет проще анализировать поведение цепей с параллельными ветвями. При работе с матрицами проводимости (Y-матрицами) важна правильная интерпретация мнимых компонентов: они определяют фазовые соотношения токов и напряжений.
При анализе цепей с использованием метода контурных токов предпочтительна форма с z, тогда как при использовании метода узловых потенциалов – форма с y, поскольку она обеспечивает прямую зависимость тока от напряжения: I = Y·U.
При проектировании фильтров и согласующих цепей важно учитывать, что максимальная передача мощности достигается, когда проводимость нагрузки комплексно сопряжена с выходной проводимостью источника.
Отличие обозначения y от g и z в электрических схемах

Обозначение y в электротехнике соответствует комплексной проводимости, выражаемой в символьной форме: Y = G + jB, где G – активная проводимость, B – реактивная. Измеряется в сименсах (См) и применяется при анализе цепей в частотной области, особенно в методе контурных токов и при расчёте эквивалентных схем с использованием двухполюсников.
g – это реальная составляющая проводимости (активная проводимость), без учёта реактивного компонента. Используется в схемах постоянного тока и в тех случаях, когда индуктивные и ёмкостные параметры несущественны. В отличие от y, g не позволяет учитывать фазовые сдвиги и реактивные потери.
z обозначает комплексное сопротивление, противоположную величину по отношению к y: Z = R + jX. Применяется для описания противодействия току в цепи. В расчётах важно не путать: Z используется для определения падения напряжения, а Y – для расчёта токов в узловом анализе.
При проектировании схем высокой частоты рекомендуется применять y для удобства расчётов параллельных соединений. В схемах низкой частоты предпочтительнее z. Для оценки только потерь – g. При выборе обозначения необходимо учитывать характер анализа: узловой метод требует Y, контурный – Z.
Применение параметра y в методе уравнений Кирхгофа

Параметр y в электротехнике обозначает проводимость (обратную величину сопротивления: y = 1/R) и активно используется при применении метода уравнений Кирхгофа в форме по узлам, особенно в матричной записи. Это упрощает решение сложных цепей с множеством ветвей и узлов.
- При составлении уравнений по первому закону Кирхгофа (закону токов) для каждого узла суммируются токи, текущие в узел и из него. Ток через ветвь выражается как произведение проводимости и разности потенциалов: I = y·(V₁ — V₂).
- Векторное уравнение для узловой анализ схемы строится с использованием матрицы проводимостей Y, где элементы рассчитываются как сумма проводимостей, сходящихся в узел (диагональ) и со знаком минус – между узлами (вне диагонали).
- Определяются потенциалы всех узлов схемы, кроме одного, выбранного в качестве опорного (нулевого).
- Строится матрица Y размером (n−1)×(n−1) для n узлов.
- Составляется система линейных уравнений вида Y·V = I, где V – вектор напряжений узлов, I – вектор токов внешних источников.
- Решается система с использованием численных методов (например, метод Гаусса или LU-разложение).
Использование параметра y особенно эффективно при работе с параллельными ветвями: вместо сложения сопротивлений используется простая алгебраическая сумма проводимостей. Это ускоряет анализ и снижает вероятность ошибок.
Роль y-параметров в анализе двухполюсников
Матричное представление позволяет описать взаимосвязь токов и напряжений на входе и выходе двухполюсника: I₁ = y₁₁U₁ + y₁₂U₂, I₂ = y₂₁U₁ + y₂₂U₂. Эти параметры представляют собой:
- y₁₁ – входную проводимость при замкнутом выходе
- y₂₂ – выходную проводимость при замкнутом входе
- y₁₂ – обратную проводимость (влияние выходного напряжения на входной ток)
- y₂₁ – прямую проводимость (влияние входного напряжения на выходной ток)
При моделировании усилителей и ВЧ-фильтров y-параметры позволяют точно учитывать переходные эффекты и взаимные влияния между портами. В отличие от z- и h-параметров, они удобны для параллельных соединений и легко измеряются с помощью векторных анализаторов цепей в диапазоне СВЧ и выше.
Для корректного применения y-параметров важна их зависимость от частоты и условий возбуждения. Их использование оправдано при анализе малосигнального режима, когда цепь можно линеаризовать вблизи рабочей точки. В этом случае матрица y становится инструментом для быстрой оценки устойчивости, согласования и усиления каскадов.
При проектировании важно минимизировать y₁₂, чтобы исключить паразитную обратную связь, и оптимизировать y₂₁ для получения требуемого коэффициента передачи. Анализ y-параметров также облегчает переход к S-параметрам при необходимости описания цепей в терминах отражения и передачи мощности.
Пример расчета схемы с использованием y-параметров
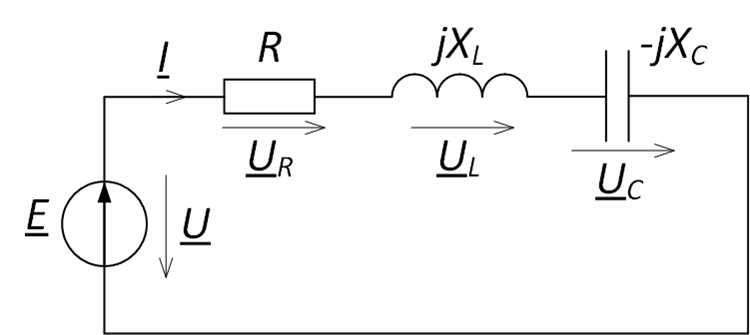
Рассмотрим двухпортовую сеть с заданными y-параметрами: y11 = 5 мСм, y12 = -1 мСм, y21 = -1 мСм, y22 = 4 мСм. На вход схемы подано напряжение U1 = 10 В, на выходе нагрузка с проводимостью YL = 2 мСм. Необходимо определить токи I1 и I2 в портах.
Запишем уравнения на основе определения y-параметров:
I1 = y11·U1 + y12·U2
I2 = y21·U1 + y22·U2
Нагрузочный ток на выходе связан с напряжением и проводимостью: I2 = YL·U2. Приравняем выражения для I2:
YL·U2 = y21·U1 + y22·U2
Отсюда выразим U2:
U2 = (y21·U1) / (YL — y22) = (-1 мСм × 10 В) / (2 мСм — 4 мСм) = (-10 мА) / (-2 мСм) = 5 В.
Подставим U2 в уравнение для I1:
I1 = 5 мСм × 10 В + (-1 мСм) × 5 В = 50 мА — 5 мА = 45 мА.
Определим I2 через нагрузку: I2 = YL × U2 = 2 мСм × 5 В = 10 мА.
Результаты: ток на входе I1 = 45 мА, на выходе I2 = 10 мА, выходное напряжение U2 = 5 В. Такой подход позволяет оперативно анализировать параметры цепей с использованием y-параметров без перехода к сложным эквивалентным схемам.
Интерпретация единиц измерения величины y
В электротехнике обозначение y часто связано с параметром проводимости или комплексной проводимостью. Единица измерения y – сименс (См), что эквивалентно обратному омму (Ом⁻¹). Значение y выражает способность элемента проводить электрический ток при заданном напряжении.
Для комплексной проводимости y = G + jB, где G – активная проводимость, измеряемая в сименсах и отражающая реальную часть тока, а B – емкостная или индуктивная составляющая, выраженная в сименсах и характеризующая реактивные свойства элемента. При анализе цепей важно учитывать фазу y, так как она влияет на соотношение между током и напряжением.
При измерении величины y необходимо применять приборы с точностью, обеспечивающей регистрацию малых значений conductance, особенно в высокочастотных цепях, где реактивная часть B может значительно превышать активную G. Рекомендуется использовать мостовые методы и сетевые анализаторы, способные выделять комплексные компоненты y.
Корректная интерпретация измерений y позволяет прогнозировать поведение элементов в реальных условиях, оптимизировать схемы с учетом потерь и реактивных эффектов, а также контролировать качество материалов и соединений в электротехнике.
Как определить y-параметры экспериментально на практике
Для измерения y-параметров (адмиттанс-параметров) двухпортового устройства необходимы точные измерения токов и напряжений при заданных условиях. Методика основана на поочередном замыкании и размыкании входных и выходных цепей с последующим измерением соответствующих токов и напряжений.
- Подготовка оборудования:
- Источник переменного напряжения с фиксированной частотой (часто 1 кГц или стандартная тестовая частота).
- Вольтметр и амперметр высокой точности или векторный анализатор параметров (VNA) для одновременного измерения комплексных значений.
- Нагрузочные резисторы с известным сопротивлением для создания граничных условий.
- Измерение y11 и y21:
- Закоротить выходные зажимы (порт 2) на землю.
- Подать напряжение U1 на вход (порт 1).
- Измерить токи I1 (на входе) и I2 (на выходе).
- Вычислить y11 = I1 / U1 при U2 = 0 и y21 = I2 / U1 при U2 = 0.
- Измерение y12 и y22:
- Закоротить входные зажимы (порт 1) на землю.
- Подать напряжение U2 на выход (порт 2).
- Измерить токи I1 (на входе) и I2 (на выходе).
- Вычислить y12 = I1 / U2 при U1 = 0 и y22 = I2 / U2 при U1 = 0.
- Рекомендации:
- Использовать согласованные нагрузки для минимизации отражений и искажений сигнала.
- Контролировать температуру приборов, так как параметры зависят от тепловых условий.
- Проводить несколько измерений для повышения точности и усреднения результатов.
- Избегать паразитных сопротивлений соединительных проводов и контактов, применяя короткие и качественные кабели.
Вопрос-ответ:
Что обозначает символ y в электротехнике и почему он важен?
В электротехнике буква y часто используется для обозначения проводимости или адмиттанса — величины, обратной сопротивлению. Это помогает анализировать электрические цепи, поскольку адмиттанс показывает, насколько легко ток проходит через элемент. Таким образом, y позволяет инженерам оценивать характеристики цепей и рассчитывать параметры при проектировании.
Какая связь между y и другими электрическими величинами, например, сопротивлением или импедансом?
Символ y обозначает адмиттанс, который является обратной величиной комплексного импеданса (Z). Если импеданс показывает общее сопротивление электрической цепи, учитывая и активную, и реактивную составляющие, то адмиттанс отражает насколько цепь проводит ток. Математически это выражается как y = 1 / Z, где Z — импеданс. Такой подход упрощает анализ цепей, особенно в переменном токе.
В каких расчетах чаще всего применяется параметр y?
Параметр y часто используют при расчёте и анализе цепей переменного тока, особенно в сетях с комплексными сопротивлениями и реактивными элементами. Он применяется в методах анализа цепей, например, в матричных методах, а также для описания поведения электрооборудования, такого как трансформаторы и линии передачи. Адмиттанс упрощает понимание протекания токов в сложных сетях.
Как изменяется значение y при изменении температуры и частоты сигнала?
Значение адмиттанса (y) зависит от физического состояния материалов и параметров цепи. При повышении температуры сопротивление обычно увеличивается, что уменьшает адмиттанс. Частота сигнала влияет на реактивные компоненты цепи: с ростом частоты изменяется емкостная и индуктивная проводимость, что сказывается на общем значении y. В результате при разных условиях адмиттанс изменяется, отражая реальные свойства цепи.
Почему иногда в схемах используют именно y-параметры, а не другие обозначения?
Использование y-параметров удобно для описания линейных цепей в частотной области, особенно когда цепь представлена как двухпортовая сеть. В таких случаях y-параметры позволяют выразить токи через напряжения на входе и выходе, что облегчает расчет и моделирование сложных систем. Это позволяет эффективно анализировать взаимодействие компонентов и их влияние на всю цепь.
Что обозначает символ y в электротехнике и почему он используется?
В электротехнике символ y часто применяется для обозначения проводимости или адмиттанса — величины, обратной сопротивлению. Он показывает, насколько легко электрический ток проходит через элемент цепи. Это значение важно для анализа сложных электрических схем, особенно в переменном токе, где учитываются как активные, так и реактивные свойства. Использование y позволяет более удобно описывать и рассчитывать параметры электрических цепей.
Как взаимосвязаны символ y и параметры цепи в переменном токе?
Символ y связан с параметрами цепи через понятие адмиттанса, который объединяет в себе проводимость и susceptance (реактивную проводимость). Величина y — это комплексное число, отражающее, как цепь проводит ток и как она реагирует на изменение напряжения. При анализе переменного тока это позволяет более точно моделировать поведение цепи, включая потери энергии и фазовые сдвиги. Зная y, можно определить ток, протекающий в цепи, и понять, как она будет работать при различных частотах сигнала.






