В чем измеряется волновое число

Волновое число (k) является важной физической величиной, описывающей количество волн, проходящих через единицу длины. Оно используется для характеристики различных типов волн, включая механические и электромагнитные. Важнейшей характеристикой волнового числа является его связь с длиной волны, что позволяет эффективно анализировать распространение волн в различных средах.

Единицей измерения волнового числа в Международной системе единиц (СИ) является 1/метр, или м^-1. Это отражает количество циклов волны на единицу длины. Волновое число обычно используется в контексте описания волновых процессов в физике, химии, а также в области оптики и квантовой механики. Например, для электромагнитных волн волновое число может быть связано с частотой и длиной волны через универсальное соотношение, полученное из уравнений Максвелла.

Использование волнового числа в расчетах и теоретических моделях играет ключевую роль при анализе различных физических процессов. В квантовой механике волновое число связано с импульсом частицы и может быть использовано для предсказания поведения системы в рамках волновых функций. Рекомендации для работы с волновым числом включают точную корректировку единиц измерений при переходе между системами единиц и использование него при анализе спектров и распространения волн.

Как волновое число связано с длиной волны?

k = 2π / λ,

где λ – это длина волны. Волновое число измеряется в радианах на метр (рад/м) и описывает, сколько полных циклов (колебаний) помещается в одном метре пространства.

Таким образом, чем меньше длина волны, тем больше волновое число. Например, для волны длиной 1 метр волновое число будет равно 2π рад/м, а для волны длиной 0,5 метра – 4π рад/м. Это соотношение позволяет точно определять свойства волн в различных областях физики, таких как оптика, акустика и квантовая механика.

Для электромагнитных волн в вакууме, например, волновое число также зависит от частоты волны через скорость света (c):

k = ω / c,

где ω – угловая частота, а c – скорость света. Это соотношение полезно при расчете характеристик волн, таких как их энергия и импульс.

Понимание связи между волновым числом и длиной волны необходимо для точного описания распространения волн и их взаимодействия с веществом. Например, в квантовой механике волновое число помогает описать состояние частиц, таких как электроны, где оно играет важную роль в вычислениях вероятностей их нахождения в определенных областях пространства.

Применение единиц волнового числа в спектроскопии

Волновое число, обозначаемое как k, представляет собой величину, обратную длине волны и измеряется в обратных метрах (м^-1). В спектроскопии оно играет ключевую роль при анализе различных видов излучений, таких как инфракрасные, видимые и ультрафиолетовые спектры.

Использование единиц волнового числа в спектроскопии помогает ускорить обработку данных. Оно напрямую связано с энергией фотонов через уравнение Эйнштейна: E = hν = hc/λ, где h – постоянная Планка, ν – частота, c – скорость света, а λ – длина волны. Применяя волновое число, можно избежать постоянных преобразований между длиной волны и частотой, что упрощает анализ спектров, особенно в области высоких энергий.

В инфракрасной спектроскопии волновое число используется для выражения частоты колебаний молекул. В отличие от традиционного подхода с длиной волны, волновое число упрощает интерпретацию результатов, так как спектры часто строятся именно в этой шкале. Например, инфракрасные спектры часто выражаются в единицах см^-1, что позволяет быстро оценить энергетические переходы молекул.

В спектроскопии молекулярных систем волновое число применяется для точной характеристики резонансных частот колебаний. Это помогает в определении состава вещества и изучении его молекулярной структуры. Использование волнового числа в данном контексте дает более наглядную картину и облегчает работу с числовыми значениями, особенно при сравнении данных разных исследовательских групп.

Применение единиц волнового числа также актуально в рамановской спектроскопии, где они помогают легко интерпретировать сдвиги частоты при взаимодействии света с молекулами. Использование волнового числа в таких измерениях позволяет точно определить спектральные линии и сдвиг Рамана, что имеет важное значение при изучении структурных изменений в материалах.

Таким образом, единицы волнового числа оказывают значительное влияние на спектроскопический анализ, улучшая точность и эффективность исследования различных спектров. Отказ от традиционной системы измерения в длине волны в пользу волнового числа повышает скорость обработки данных и минимизирует возможные ошибки при интерпретации сложных спектральных характеристик.

Как преобразовать волновое число в частоту и наоборот?

Волновое число и частота связаны через скорость распространения волны. Для преобразования между этими величинами необходимо учитывать характер волны и её среду распространения.

Частота (ν) волны связана с её волновым числом (k) через скорость распространения (v) по следующей формуле:

ν = v * k

Для преобразования волнового числа в частоту, нужно умножить волновое число на скорость волны в данной среде. Например, для звуковых волн в воздухе, скорость звука примерно равна 343 м/с при температуре 20°C. Таким образом, если волновое число составляет 50 м⁻¹, то частота будет равна:

ν = 343 м/с * 50 м⁻¹ = 17150 Гц

Чтобы преобразовать частоту в волновое число, используется обратная формула:

k = ν / v

Для того чтобы найти волновое число, нужно частоту поделить на скорость распространения волны. Например, для световой волны с частотой 5 * 10¹⁴ Гц в вакууме (где скорость света c = 3 * 10⁸ м/с), волновое число будет равно:

k = (5 * 10¹⁴ Гц) / (3 * 10⁸ м/с) = 1.67 * 10⁶ м⁻¹

Таким образом, в любой системе можно легко преобразовать волновое число в частоту и наоборот, зная скорость распространения волны в данной среде.

Роль волнового числа в анализе квантовых явлений

Волновое число (k) напрямую связано с импульсом микрочастиц согласно соотношению Де Бройля: p = ħk, где ħ – приведённая постоянная Планка. Это позволяет описывать квантовое состояние частицы через волновую функцию, у которой пространственная зависимость определяется именно волновым числом.

В спектроскопии волновое число используется для точного определения энергетических уровней, поскольку энергия фотонов выражается через E = ħω = ħck, где c – скорость света, ω – угловая частота. Измерения с разрешением до 0.01 см⁻¹ обеспечивают выявление тонких структур спектров молекул и атомов.

При анализе квантовых колебаний и волн де Бройля волновое число характеризует длину волны частицы (λ = 2π/k), что критично для оценки вероятностного распределения и туннельных эффектов в потенциалах. Волновое число также выступает параметром в уравнениях Шредингера для определения собственных значений энергии и формы волновых функций.

В квантовой механике конденсированных сред волновое число служит ключевым параметром для описания зонной структуры и энергетических дисперсий электронов в кристаллической решётке. Максимальные значения k ограничены размером первой зоны Бриллюэна, что влияет на плотность состояний и электронные свойства материалов.

Для расчётов сдвигов уровней энергии в квантовых системах и оценки эффектов взаимодействия частиц рекомендуется использовать волновое число в единицах см⁻¹ или нм⁻¹, что упрощает сравнение экспериментальных данных и теоретических моделей.

Единицы волнового числа в расчетах распространения волн

Волновое число характеризует количество волн на единицу длины и определяется как обратная величина длины волны. В международной системе единиц (СИ) волновое число измеряется в метрах в степени минус один (м⁻¹), что соответствует количеству волн на метр.

В задачах распространения электромагнитных и акустических волн чаще всего используется именно эта единица, так как она напрямую связана с длиной волны λ через формулу k = 2π/λ, где k – волновое число. Для практических расчетов важно сохранять размерность м⁻¹, чтобы корректно сопоставлять параметры среды и геометрические характеристики волн.

В спектроскопии распространена единица см⁻¹, особенно при анализе инфракрасных и ультрафиолетовых спектров. При этом 1 см⁻¹ = 100 м⁻¹. Такой масштаб удобен для обработки экспериментальных данных и упрощает сравнение с энергетическими уровнями в химии и физике твердого тела.

При расчетах дисперсии волн в волноводах и оптических системах волновое число часто выражается в безразмерной форме, нормированной на длину волны в вакууме. Это позволяет учитывать эффект среды и упрощает численное моделирование. Рекомендуется чётко фиксировать выбранную размерность во избежание ошибок при переводе между разными системами.

Для волн с высокой частотой и малыми длинами, например, в рентгеновской и гамма-спектроскопии, используется волновое число в нанометрах в степени минус один (нм⁻¹) или ангстремах в степени минус один (Å⁻¹). Это обеспечивает удобство записи и точность вычислений на соответствующих масштабах.

В расчетах параметров распространения волн важна единообразность измерений волнового числа. При смешении единиц (м⁻¹, см⁻¹, нм⁻¹) необходимо использовать точные коэффициенты пересчета и проверять размерность в формулах, чтобы избежать накопления погрешностей.

Использование волнового числа для определения свойств материала

Для анализа оптических свойств материалов волновое число может быть использовано для точной настройки параметров, таких как преломление, поглощение и отражение. Например, при измерении коэффициента поглощения материала для определённой длины волны, волновое число помогает определить, как быстро волна убывает в веществе, что важно для разработки оптических фильтров и покрытия, особенно в инфракрасной области.

В механике материалов волновое число тесно связано с колебаниями атомов и молекул, что помогает исследовать упругие свойства вещества. Использование волнового числа при анализе фононных спектров позволяет выявить особенности кристаллической решётки, её дефекты и аномалии, что непосредственно влияет на теплопроводность материала. Так, например, для полупроводников волновое число может быть использовано для изучения фононных взаимодействий, что важно для создания более эффективных термоэлектрических материалов.

Важным применением волнового числа является также в области акустики. В звуковых волнах волновое число позволяет вычислить скорость распространения звука через различные материалы. Это полезно при проектировании конструкций с высокой акустической изоляцией или при создании новых материалов для звукопоглощения. Например, знание волнового числа в акустическом спектре помогает определить, на каких частотах материал будет эффективно поглощать звук.

Таким образом, волновое число является универсальным инструментом для глубокого анализа и точного предсказания поведения материала при различных типах волн, будь то свет, звук или термические волны. Оно служит связующим звеном между теоретическими моделями и практическими измерениями, играя важную роль в разработке новых технологий.

Практические задачи: как выбрать подходящие единицы для волнового числа?

Волновое число выражается как отношение 2π к длине волны, и его единица измерения в системе СИ – метры в минус первой степени (м⁻¹). Однако в зависимости от специфики задачи могут быть удобны и другие системы единиц. Рассмотрим несколько типов задач и подходящие единицы измерения для них.

1. Для задач с короткими волнами (например, в оптике или рентгеновской области)

Единица измерения: см⁻¹ или мм⁻¹.
Подходит для работы с короткими волнами, например, при анализе рентгеновских лучей. Такие единицы упрощают выражение волнового числа, так как длина волны в таких областях может быть очень маленькой (от десятков нанометров до фемтометров).
При расчетах на этих длинах волн важно иметь единицу измерения, которая будет практичной и позволит избежать использования чрезмерно малых чисел.

2. Для задач в области акустики

Единица измерения: м⁻¹.
В акустике длина волны звуковых волн в воздухе часто измеряется в метрах. Для таких задач стандартная единица м⁻¹ подходит лучше всего.
Например, для звуковых волн в диапазоне частот от 20 Гц до 20 кГц длина волны будет варьироваться от нескольких десятков метров до нескольких миллиметров. В этом случае использование метра для волнового числа будет наиболее удобным.

3. Для задач в области атомной и молекулярной физики

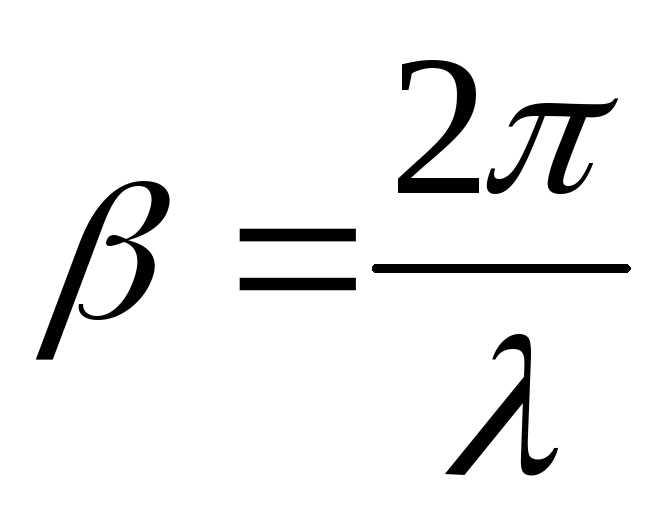
Единица измерения: см⁻¹ или 1/эВ (для энергии).
В молекулярной спектроскопии часто используют единицу см⁻¹, так как спектры переходов между энергетическими уровнями атомов или молекул обычно представлены именно в таких единицах.
Для учета энергии переходов удобно использовать связь между волновым числом и энергии через уравнение E = h * c * k, где h – постоянная Планка, c – скорость света, k – волновое число. В этом случае единица измерения волнового числа в 1/эВ может быть полезной для молекулярных спектров.

4. Для задач в теоретической физике и математике

Единица измерения: любые подходящие единицы системы, в зависимости от используемой модели.
Для теоретических расчетов часто используется абстрактная система единиц или система, связанная с масштабами работы задачи. В таких случаях волновое число может быть выражено в безразмерных величинах или в единицах, удобных для работы с конкретной моделью.

5. Для работы с элементарными частицами

Единица измерения: 1/м (метр в минус первой степени), но иногда используется более удобный формат, например, 1/км.
Для высокоэнергетических частиц, как правило, предпочтительнее использовать единицы измерения в метрах или километрах для удобства работы с длинными волнами.

6. Особенности выбора единиц для практических расчетов

При переходе от одной системы единиц к другой важно помнить, что выбор единиц измерения влияет на точность вычислений и интерпретацию результатов. Переходя от СИ к другим системам, следует учитывать коэффициенты перевода.
Для практических задач в лабораториях и при измерениях часто используется единица см⁻¹, так как она упрощает работу с небольшими величинами.
Для задач, связанных с большими масштабами, таких как астрономия, могут быть удобны более крупные единицы, например, м⁻¹ или км⁻¹.

Выбор единиц волнового числа всегда зависит от масштаба задачи и области применения. Правильное использование единиц измерения помогает существенно упростить расчетные процессы и сделать результаты более понятными и интерпретируемыми для научных исследований и прикладных разработок.

Вопрос-ответ:

Что такое волновое число и как оно связано с длиной волны?

Волновое число — это физическая величина, которая описывает количество волн, приходящихся на единицу длины. Оно определяет, сколько полных волн помещается на единицу расстояния. Формула для волнового числа выражается как \(k = \frac{2\pi}{\lambda}\), где \(\lambda\) — длина волны. Чем больше волновое число, тем короче волна, и наоборот. Это количество волн позволяет связать различные характеристики волн, такие как энергия и импульс.

Какие единицы измерения волнового числа используются в физике?

Волновое число измеряется в обратных метрах (\(м^{-1}\)) или радианах на метр. Это связано с тем, что волновое число \(k\) является величиной, которая описывает угловую частоту волны, и её измерение зависит от длины волны. В международной системе единиц (СИ) волновое число выражается в метрах в минус первой степени (м\(^{-1}\)), так как оно является обратной величиной длины волны.

Как волновое число связано с другими характеристиками волн, например, с частотой или энергией?

Волновое число непосредственно связано с длиной волны, а следовательно, с другими характеристиками, такими как энергия и частота. Частота волны \(\nu\) и волновое число \(k\) могут быть связаны через скорость распространения волны \(v\) с помощью формулы \(\nu = v k\). Энергия частицы или фотона также может быть выражена через волновое число с помощью формулы \(E = \hbar v k\), где \(\hbar\) — редуцированная постоянная Планка, а \(v\) — скорость волны. Чем больше волновое число, тем выше энергия.

Может ли волновое число быть отрицательным?

Волновое число в физике не может быть отрицательным в контексте стандартных колебательных волн, поскольку оно связано с пространственным распределением волн, и представляет собой количество волн в единице длины, что всегда положительно. Однако могут быть ситуации, когда в теоретических расчетах или в определенных моделях (например, в квантовой механике или при описании обратных волновых процессов) можно встретить отрицательное волновое число, что вносит определённые особенности в поведение волны, такие как её распространение или интерференционные эффекты.

Как использовать волновое число при решении задач в оптике или акустике?

Волновое число играет важную роль в различных областях физики, таких как оптика и акустика. Например, в оптике волновое число используется для анализа распространения света в разных средах, где оно связано с рефракцией, интерференцией и дифракцией. В акустике волновое число помогает понять, как звуковые волны распространяются в воздухе или других веществах. Для расчета, например, распространения звуковых волн в трубе или её резонансных частот можно использовать зависимость волнового числа от скорости звука и длины волны, что помогает предсказывать акустические явления.

Что такое волновое число и каковы его единицы измерения в физике?

Волновое число — это физическая величина, которая описывает количество волн, приходящихся на единицу длины. Оно связано с длиной волны и частотой волны и используется для описания распространения волн, таких как световые или звуковые. Единицы измерения волнового числа в Международной системе единиц (СИ) — это обратные метры (м⁻¹). Таким образом, волновое число указывает, сколько волн помещается в одном метре пространства.