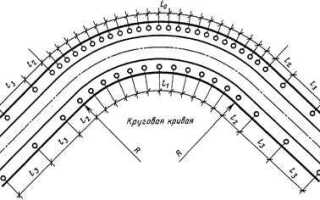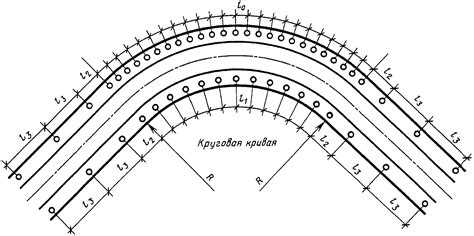
Точное определение радиуса закругления арочной конструкции критично при проектировании проёмов, перекрытий и элементов купольного типа. Ошибки в расчёте могут привести к перерасходу материалов, нестабильности конструкции и несоответствию нормативным требованиям. Радиус влияет на распределение нагрузок, выбор материала, а также на технологичность производства и монтажа.
Для определения радиуса используют геометрические зависимости, основанные на параметрах дуги: высоте подъёма (стреле прогиба) и ширине пролёта. На практике наиболее распространён формула для круговой арки: R = (L² + 4h²) / (8h), где L – пролёт, h – подъём. Этот метод применим при условии симметричной формы и отсутствии деформаций по вертикали.
При использовании нестандартных форм – эллиптических или многоцентровых арок – стандартные формулы не подходят. В таких случаях прибегают к численным методам: аппроксимации кривой по заданным точкам с использованием CAD-систем или аналитических выражений для построения профиля. Результат зависит от плотности точек и точности ввода исходных данных.
На этапе проектирования рекомендуется закладывать радиус с учётом технологических ограничений: минимальный изгиб профиля без остаточной деформации, радиус гибки для конкретного материала, наличие допуска на отклонения. Например, для металлического профиля радиус не должен быть меньше 100–150 мм в зависимости от толщины и марки стали.
В завершение, важно учитывать, что даже при точном расчёте радиуса необходимо его проверять на прочность, устойчивость и соответствие архитектурным требованиям. Расчёт радиуса – это не только геометрическая задача, но и инженерная оценка с учётом эксплуатационных и производственных факторов.
Как определить тип арки для последующего расчёта радиуса

Перед началом расчётов необходимо точно классифицировать арку по геометрической форме. Наиболее распространённые типы: полукруглая, сегментная, трёхцентровая, стрельчатая и параболическая.
Полукруглая арка определяется равной высотой и половиной пролёта. Радиус совпадает с половиной пролёта. Если пролёт 4 м, радиус – 2 м.
Сегментная арка ниже полукруглой. Радиус вычисляется по хорде (ширине пролёта) и стрелке подъёма. При известной высоте и пролёте используется формула: R = (h/2) + (L² / 8h), где L – пролёт, h – высота подъёма.
Трёхцентровая арка состоит из трёх дуг с разными центрами. Для идентификации требуется анализ контура: центральная часть – более плоская, боковые дуги – круче. Необходимо определить координаты сопряжения для дальнейшего определения каждого из трёх радиусов.
Стрельчатая арка характеризуется острым сводом. Её контур формируют две дуги, пересекающиеся в вершине. Требуется определить радиус каждой дуги отдельно, исходя из симметрии и высоты свода.
Параболическая арка не имеет постоянного радиуса. Распознаётся по уравнению y = ax² при симметричном контуре и равномерном подъёме. Радиус кривизны рассчитывается в конкретной точке по формуле: R = [1 + (dy/dx)²]³⁄² / |d²y/dx²|.
Для точного определения типа арки рекомендуется измерить пролёт, высоту подъёма и визуально или инструментально проанализировать форму кривой. Без этой классификации расчёт радиуса будет некорректным.
Формулы для вычисления радиуса круглой арки по заданной ширине и высоте
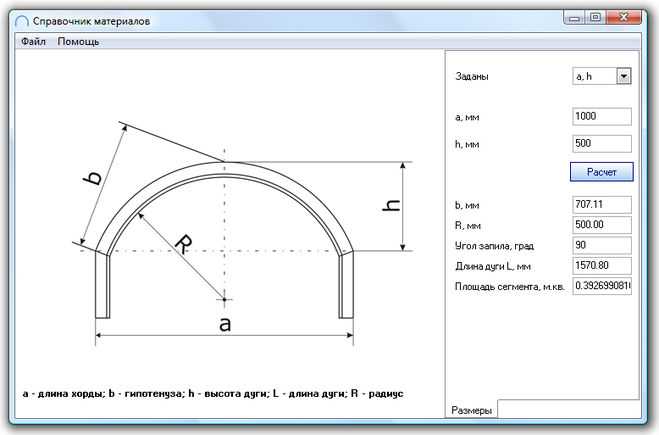
Для круглой арки, представляющей собой дугу окружности, радиус R можно определить по заданной ширине пролёта L и высоте подъёма H от основания до вершины арки. Применяется следующая формула:
R = (L² / 8H) + (H / 2)
Где:
R – радиус окружности,
L – горизонтальный пролёт между опорами (в основании арки),
H – высота подъёма дуги от основания до наивысшей точки.
Если известен только пролет и предполагается полукруглая арка, используется упрощённая формула:
R = L / 2
Однако в большинстве инженерных задач используется первая формула, так как она позволяет рассчитать радиус для произвольной высоты, не ограниченной полукруглой формой. Для точности измерений L и H должны быть в одинаковых единицах.
Перед применением формулы важно убедиться, что конструкция действительно представляет собой часть окружности, а не эллиптическую или параболическую дугу. В противном случае расчёт радиуса по данной формуле приведёт к значительным погрешностям.
Расчёт радиуса трёхцентровой арки с использованием координатных точек
Для точного определения радиусов трёхцентровой арки необходимо задать координаты четырёх ключевых точек: начальной (A), конечной (B) и двух вершинных точек сопряжения (C и D), через которые должны проходить дуги. Координаты каждой точки задаются в виде (x, y) в декартовой системе.
Первым шагом рассчитываются расстояния между соседними точками: AB, AC, CD и DB. Используется формула Евклидова расстояния:
d = √((x₂ - x₁)² + (y₂ - y₁)²).
Затем определяются углы между отрезками, формирующими центры дуг. Углы между отрезками AC и CD, а также между CD и DB, рассчитываются через скалярное произведение и нормализацию векторов.
На основании найденных углов и расстояний строятся серединные перпендикуляры к отрезкам AC и DB. Точки пересечения этих перпендикуляров с линиями сопряжения (AC–CD и CD–DB) определяют центры окружностей, образующих трёхцентровую арку.
Радиусы определяются как расстояния от центров построенных окружностей до точек сопряжения (C и D). Для трёх дуг арки определяются три радиуса: R₁ (дуга AC), R₂ (дуга CD) и R₃ (дуга DB). Радиусы вычисляются по формуле:
R = √((x_c - x₀)² + (y_c - y₀)²), где (x_c, y_c) – координаты центра, (x₀, y₀) – координаты точки сопряжения.
Для проверки корректности расчёта необходимо убедиться в непрерывности касания между дугами в точках C и D. Это обеспечивается совпадением касательных направлений, что можно проверить через равенство углов между радиусами и соответствующими отрезками касания.
Рекомендуется использовать специализированное ПО или системы автоматизированного проектирования для минимизации погрешностей при работе с реальными координатами.
Определение радиуса закругления при проектировании арки в прямоугольном проёме
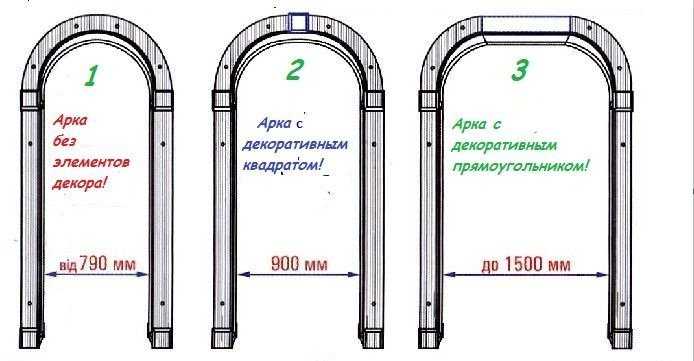
При проектировании арки в прямоугольном проёме основной параметр – радиус закругления, напрямую зависящий от ширины проёма и желаемой высоты подъёма арки. Для полукруглой арки радиус равен половине ширины проёма: при ширине 1200 мм радиус будет 600 мм.
В случае сегментной арки радиус рассчитывается по формуле: R = (h / 2) + (b² / (8h)), где h – подъём арки, b – ширина проёма. Например, при ширине 1500 мм и подъёме 300 мм радиус составит: R = (300 / 2) + (1500² / (8 × 300)) = 150 + 937.5 = 1087.5 мм.
Если требуется точное сопряжение арки с вертикальными стойками, минимальный радиус должен обеспечивать касание дуги с прямыми участками без образования изломов. При малом подъёме (менее 10% ширины) формируется широкая и пологая арка, что требует увеличения радиуса для сохранения геометрической устойчивости и эстетики.
Не рекомендуется использовать произвольные значения радиуса без расчёта – это может привести к нарушению симметрии и искажению нагрузки на несущие элементы. Оптимальный радиус обеспечивает равномерное распределение давления на арочную часть и смежные конструкции.
Проектирование необходимо выполнять с использованием CAD-систем или геометрических построений, основанных на точных параметрах проёма. Пренебрежение расчётом приводит к деформациям при эксплуатации и снижению ресурса конструкции.
Учёт строительных допусков при расчёте радиуса арочной конструкции
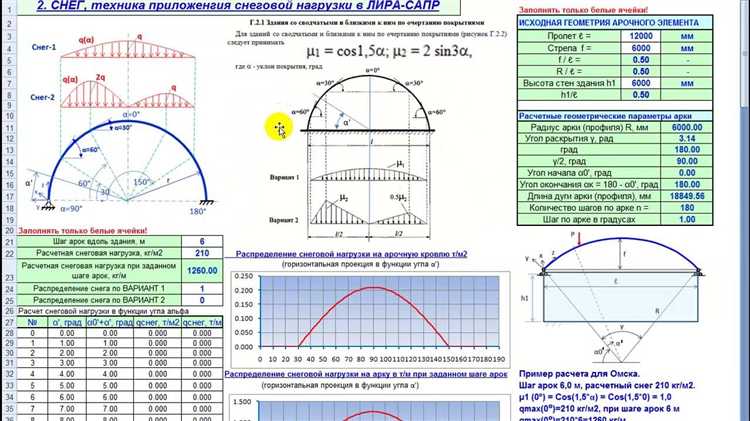
При расчёте радиуса арочной конструкции необходимо учитывать допуски, обусловленные технологией монтажа и отклонениями в производстве элементов. Например, при проектировании стальных арок стандартный допуск на отклонение от проектного радиуса по ГОСТ 23118-2012 составляет ±5 мм на длине 1 метра, что может существенно повлиять на итоговую геометрию при больших пролётах.
Для деревянных арок необходимо учитывать усушку и возможные изменения формы в пределах допустимых значений, регламентированных СП 64.13330.2017. Отклонения могут достигать ±3 мм на каждый метр дуги, что требует корректировки расчётного радиуса на этапе проектирования с учётом коэффициента усадки, зависящего от породы древесины и условий эксплуатации.
В железобетонных арках значение имеет точность опалубки и армирования. В соответствии с СП 52-101-2003, допуски по изгибу радиуса не должны превышать ±10 мм при длине дуги до 10 м. При превышении этого значения требуется перерасчёт с учётом фактического отклонения, зафиксированного при натурных измерениях после демонтажа опалубки.
Рекомендуется включать допуски в проектную документацию в виде корректирующего коэффициента, применяемого к расчётному радиусу. Например, для металлической арки длиной 12 м целесообразно закладывать запас 0,6% от теоретического радиуса, что эквивалентно корректировке на ±72 мм.
Игнорирование допусков приводит к накоплению погрешностей при монтаже, особенно при стыковке нескольких арочных элементов. Поэтому в расчётах необходимо учитывать не только теоретическую геометрию, но и реальные производственные и монтажные условия.
Как перевести размеры с чертежа в реальные величины для расчёта радиуса
Для точного расчёта радиуса закругления арочной конструкции необходимо корректно интерпретировать размеры с чертежа и привести их к реальным масштабам. Следуйте следующим шагам:
- Определите масштаб чертежа. Обычно он указан в виде отношения (например, 1:50, 1:100). Если масштаб не указан, измерьте известный размер на чертеже и сравните с реальным.
- Измерьте необходимые линейные величины на чертеже с помощью штангенциркуля или линейки с делениями в миллиметрах.
- Переведите измеренное значение в реальные размеры, умножив результат на коэффициент масштаба. Например, при масштабе 1:100 значение 25 мм на чертеже соответствует 2500 мм в реальности.
- При работе с радиусами закруглений учитывайте особенности чертежа: радиусы могут быть указаны явно, а могут требовать вычисления из габаритов дуги или сектора. В этом случае:
- Измерьте длину дуги и высоту стрелы дуги.
- Используйте формулу радиуса: R = (L² / 8h) + (h / 2), где L – длина дуги, h – высота стрелы.
- Проверяйте единицы измерения – на чертеже могут использоваться миллиметры, сантиметры или метры. Для расчётов лучше приводить всё к одной системе (мм или м).
- При цифровой обработке чертежей используйте программные инструменты с функцией масштабирования, чтобы избежать погрешностей ручных измерений.
Точная конвертация размеров с чертежа в реальные величины обеспечит корректность дальнейших инженерных расчётов и минимизирует ошибки при изготовлении арочной конструкции.
Проверка полученного радиуса на соответствие проектным требованиям
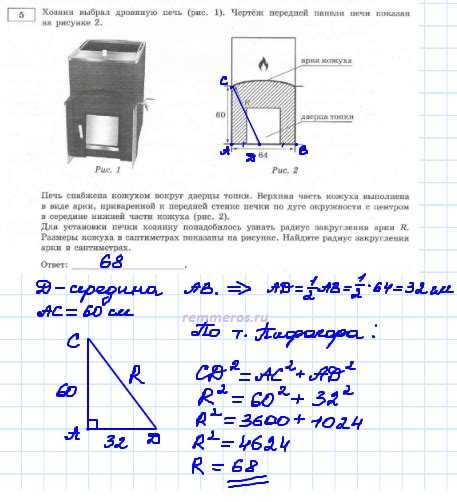
Для проверки радиуса закругления арочной конструкции необходимо сравнить рассчитанное значение с нормативными и проектными параметрами. Минимально допустимый радиус определяется техническими стандартами и зависит от типа конструкции, материала и эксплуатационных нагрузок.
Первым этапом является сверка радиуса с предельным значением, указанным в проектной документации. Если радиус меньше допустимого, требуется пересчет геометрии или подбор другого типа арки. Недостаточный радиус увеличивает напряжения в материале и может привести к преждевременному износу или деформации.
Далее проверяется соответствие радиуса критериям технологичности изготовления. Для металлических конструкций радиус не должен быть меньше толщины листа более чем в 3 раза, чтобы избежать чрезмерных деформаций при гибке. В бетоне минимальный радиус ограничен размерами опалубки и армирования.
Следующий шаг – оценка влияния радиуса на несущую способность. Радиус влияет на распределение усилий: при увеличении радиуса снижаются концентрации напряжений, что повышает долговечность. В проектах с высокой нагрузкой рекомендуется увеличивать радиус не менее чем на 10% от расчетного, если геометрия позволяет.
Заключительная проверка – соответствие радиуса архитектурным требованиям. Здесь важно учитывать визуальное восприятие и гармоничность формы. При значительном отклонении от проектных значений требуется согласование с архитектором и, при необходимости, корректировка проекта.
Вопрос-ответ:
Как определить радиус закругления арочной конструкции для обеспечения её прочности?
Радиус закругления рассчитывается с учётом механических нагрузок и материалов конструкции. Обычно используется формула, связывающая геометрические параметры арки с её прогибами и напряжениями. Правильный радиус позволяет равномерно распределить нагрузки, снижая риск деформации и разрушения.
Какие параметры влияют на выбор радиуса закругления арки в строительстве?
Основные параметры включают ширину пролёта, высоту арки, свойства материала и предполагаемые нагрузки (например, ветровые или снеговые). Также учитывается назначение конструкции — временная или постоянная, и технологические ограничения при изготовлении.
Можно ли использовать стандартные формулы для расчёта радиуса закругления арочных конструкций из разных материалов?
Формулы могут служить базой, однако для различных материалов (бетон, металл, дерево) требуется учитывать их особенности, такие как модуль упругости и предел прочности. Для точных расчётов лучше применять методы, учитывающие свойства конкретного материала, чтобы избежать ошибок и повысить безопасность конструкции.
Как влияет изменение радиуса закругления на устойчивость арочной конструкции?
Увеличение радиуса обычно уменьшает внутренние напряжения, делая конструкцию более устойчивой к деформациям. Слишком малый радиус может привести к концентрации напряжений и повышенному риску повреждений. Баланс между радиусом и прочими параметрами помогает оптимизировать конструкцию.
Какие методы расчёта радиуса закругления используются для арок сложной формы?
Для арок с нестандартной геометрией применяются численные методы, например, конечные элементы или программное моделирование. Такие подходы позволяют учесть неоднородность нагрузки и материалы с переменными характеристиками, обеспечивая более точный результат по сравнению с классическими аналитическими формулами.