На что действует сила лоренца

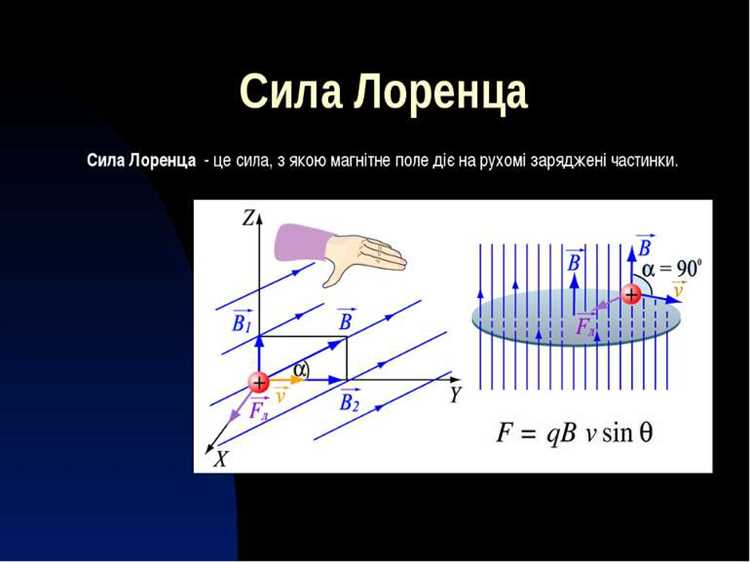
Сила Лоренца – это результирующее воздействие электрического и магнитного полей на движущиеся заряженные частицы. Вектор силы определяется выражением F = q(E + v × B), где q – заряд частицы, E – напряжённость электрического поля, v – скорость частицы, а B – вектор магнитной индукции. Эта сила лежит в основе множества физических явлений и широко используется в прикладных устройствах: от ускорителей частиц до систем управления плазмой.

Наиболее заметно действие силы Лоренца проявляется при высоких скоростях движения заряженных объектов в зонах с сильным магнитным полем. Примером служат траектории электронов в электронно-лучевых трубках и циклотронных установках. В случае равномерного магнитного поля частица движется по окружности радиусом R = mv / (qB), что позволяет точно рассчитывать параметры систем магнитного удержания и диагностики пучков.

При проектировании электромагнитных устройств важно учитывать не только величину силы Лоренца, но и её направление. Для этого применяется правило правой руки: если расположить пальцы по направлению скорости, а ладонь – вдоль магнитного поля, то отогнутый большой палец укажет направление силы, действующей на положительный заряд. Это правило критически важно для ориентации элементов в магнитных сепараторах, масс-спектрометрах и магнитогидродинамических генераторах.

Особое внимание уделяется влиянию силы Лоренца в плазменных средах, где движение ионов и электронов одновременно подчиняется сложным конфигурациям внешних полей. В таких системах требуется анализ динамики с учётом пространственной неоднородности полей и коллективных эффектов. Расчёты на основе уравнений движения с силой Лоренца позволяют моделировать процессы в термоядерных реакторах и управлять параметрами плазменных пучков в технологических установках.

Движение заряженных частиц в магнитном поле прямого проводника

Прямолинейный проводник с током создает вокруг себя магнитное поле с радиально замкнутыми силовыми линиями, направленными по правилу правого винта. Величина магнитной индукции уменьшается обратно пропорционально расстоянию от оси проводника: B = (μ₀I)/(2πr), где I – сила тока, r – расстояние от проводника, μ₀ – магнитная постоянная.

Заряженная частица, перемещающаяся вблизи такого проводника, испытывает действие силы Лоренца, вектор которой определяется выражением F = q(v × B). Направление этой силы перпендикулярно как скорости частицы, так и вектору магнитной индукции.

Тип движения частицы зависит от:

• знака заряда (электроны и ионы отклоняются в противоположные стороны);
• направления скорости относительно проводника (параллельно, перпендикулярно или под углом);
• расстояния до проводника (влияние поля экспоненциально уменьшается с ростом r);
• массы и начальной кинетической энергии частицы.

Если частица движется параллельно проводнику, но не вдоль линии тока, траектория принимает форму спирали вокруг проводника с постепенно изменяющимся радиусом. При движении перпендикулярно – возникает закрученное отклонение в сторону, формируя дугу с переменным радиусом.

На практике это важно при проектировании:

1. магнитных ловушек для плазмы (например, в управляемом термоядерном синтезе);
2. сенсоров тока на основе эффекта Холла;
3. разгрузочных путей для защиты чувствительных электронных компонентов от пучков заряженных частиц;
4. систем навигации и управления в ионных двигателях.

Контроль конфигурации магнитного поля и точное моделирование движения частиц позволяют минимизировать паразитные отклонения и повысить эффективность устройств, использующих проводники с током вблизи свободных зарядов.

Поведение ионов в плазме при наличии магнитного поля

При воздействии магнитного поля на ионы в плазме возникает направленное движение, обусловленное действием силы Лоренца. Вектор этой силы перпендикулярен как вектору скорости иона, так и вектору магнитной индукции. Это приводит к тому, что ионы совершают спиральное движение вокруг силовых линий магнитного поля с характерной циклотронной частотой.

Циклотронная частота определяется выражением: ω_c = qB/m, где q – заряд иона, B – напряженность магнитного поля, m – масса иона. При фиксированной индукции более легкие ионы (например, ионы водорода) движутся по меньшим радиусам и с большей частотой, чем более тяжелые ионы (например, ионы кислорода).

Радиус спиральной траектории (ламорова орбита) рассчитывается как r_L = mv_⊥ / qB, где v_⊥ – поперечная составляющая скорости иона. Чем сильнее магнитное поле, тем меньше радиус орбиты, и тем выше степень ограничения движения ионов поперек поля.

В неоднородном магнитном поле ионы испытывают дополнительные дрейфы. Наиболее характерен градиентный дрейф, скорость которого выражается как: v_∇B = (mv_⊥²) / (2qB³) × (B × ∇B). Этот эффект важен при моделировании удержания плазмы в магнитных ловушках и токамаках.

Продольное движение ионов вдоль магнитных силовых линий, в отсутствие электрического поля, остается практически неограниченным. Однако наличие параллельной составляющей электрического поля вызывает ускорение ионов вдоль поля, что критически влияет на устойчивость плазмы и формирование токов.

Для эффективного управления поведением ионов в плазме применяют комбинации статических и переменных магнитных полей. Это позволяет влиять на параметры распределения ионов, подавлять нежелательные потери на стенки реактора и формировать устойчивые конфигурации магнитного удержания.

Сила Лоренца в электронно-лучевых трубках и её влияние на пучок

В электронно-лучевых трубках (ЭЛТ) основное действие на поток электронов оказывает сила Лоренца, возникающая при взаимодействии движущихся зарядов с внешними магнитными и электрическими полями. Электроны в таких системах разгоняются электрическим полем, после чего попадают в зону действия магнитного поля, создаваемого отклоняющими катушками.

Магнитное поле катушек ориентировано перпендикулярно направлению движения электронов, что приводит к возникновению силы Лоренца, направленной поперечно траектории. В результате электронный пучок отклоняется от прямолинейного пути, и его точка попадания на люминесцентный экран изменяется. Это позволяет формировать изображение или проводить пространственный анализ сигналов, как в осциллографах.

Угол отклонения пучка пропорционален силе тока в отклоняющих катушках и индукции магнитного поля. Повышение напряжения ускоряющего электрода увеличивает кинетическую энергию электронов, снижая отклоняемость пучка при фиксированном магнитном поле. Поэтому требуется точная синхронизация параметров для корректного формирования изображения или измерения.

При наличии внешних магнитных возмущений (например, от трансформаторов) отклонение пучка становится неконтролируемым. Это приводит к дрожанию, смещению или искажению изображения. Чтобы минимизировать такие эффекты, корпуса ЭЛТ экранируются ферромагнитными материалами, а в высокоточных приборах применяются системы активной компенсации поля.

Сила Лоренца также влияет на фокусировку пучка. Магнитные линзы формируют необходимую геометрию поля, чтобы удерживать электроны в узком пучке. Несоосность элементов или перегрев катушек приводит к расфокусировке, что снижает разрешающую способность устройства.

Точное моделирование силы Лоренца в ЭЛТ необходимо для проектирования современной вакуумной электроники и диагностики плазменных потоков. Расчёты учитывают пространственное распределение поля, энергию электронов и геометрию траектории. Программные симуляторы позволяют подбирать оптимальные параметры для заданных условий эксплуатации.

Отклонение элементарных частиц в циклотроне и синхротроне

Циклотрон и синхротрон – ускорители, в которых элементарные частицы движутся по криволинейной траектории под действием силы Лоренца. При этом отклонение траектории зависит от энергии частицы, магнитной индукции и геометрии установки.

В циклотроне движение заряженной частицы происходит по спирали, радиус которой увеличивается с ростом её скорости. Сила Лоренца, действующая перпендикулярно к вектору скорости и к вектору магнитной индукции, обеспечивает центростремительное ускорение:

• Радиус траектории определяется по формуле r = mv / (qB), где m – масса частицы, v – её скорость, q – заряд, B – индукция магнитного поля.
• С увеличением энергии частицы её радиус возрастает, требуя расширения диаметрических пластин ускорителя.
• Отклонение в циклотроне неравномерное, особенно при приближении к релятивистским скоростям, где эффект увеличения массы становится критичным.

Синхротрон работает на принципиально ином подходе: радиус орбиты частицы остаётся постоянным, а магнитное поле синхронизируется с её нарастающей энергией. Это устраняет проблему рассогласования между частотой и орбитой:

1. Магнитное поле увеличивается одновременно с ростом скорости частицы, удерживая её на одной и той же траектории.
2. Отклонение здесь управляемо и строго контролируемо: точность настройки магнитных катушек определяет стабильность орбиты.
3. Для электронов и позитронов значительное тормозное излучение (синхротронное излучение) становится ограничивающим фактором при высоких энергиях.

В обоих типах ускорителей направление и величина силы Лоренца критически влияют на точность удержания частиц на орбите. Нарушение синхронизации магнитного поля и энергии приводит к резкому отклонению частиц, что требует автоматизированной коррекции магнитных параметров в режиме реального времени.

Практическое применение этой зависимости лежит в системах медицинской протонной терапии, где точность отклонения пучка определяет глубину проникновения в ткань, а также в физике высоких энергий при исследованиях элементарных взаимодействий.

Взаимодействие силы Лоренца с токопроводящими пластинами в магнитометрах

В магнитометрах, основанных на индукционном принципе, применяются тонкие токопроводящие пластины (чаще всего медные или алюминиевые), через которые протекает измерительный ток. При помещении таких пластин в магнитное поле перпендикулярно направлению тока возникает сила Лоренца, действующая на заряды внутри проводника.

Сила Лоренца вызывает отклонение траектории электронов, что приводит к перераспределению заряда на гранях пластины. Это перераспределение создает поперечное электрическое поле, компенсирующее начальное отклонение. В результате формируется так называемое напряжение Холла, величина которого прямо пропорциональна плотности магнитного потока и силе тока, проходящего через пластину.

При проектировании магнитометров важно учитывать геометрию пластин: толщина должна быть минимальной для уменьшения индуктивных помех, а ширина и длина – достаточными для обеспечения измерительной чувствительности. Материал пластин выбирается с учетом высокой подвижности носителей заряда и низкого сопротивления, что позволяет увеличить сигнал Холла без существенного нагрева.

Для стабилизации параметров измерения пластины размещаются в термостатированных камерах, исключающих температурные дрейфы. Дополнительно может использоваться экранирование от внешних электромагнитных помех, особенно в приборах, применяемых в геофизике и аэрокосмических системах.

В современных твердотельных магнитометрах пластина часто интегрирована с полупроводниковыми сенсорами, где измерение напряжения Холла осуществляется с микровольтовой точностью. Это обеспечивает устойчивую регистрацию слабых магнитных полей вплоть до десятков нанотесла, что критично, например, при регистрации геомагнитных аномалий или в навигационных системах на основе магнитного поля Земли.

Работа силы Лоренца в системах магнитной левитации

В системах магнитной левитации сила Лоренца действует на движущиеся заряды в проводящих элементах, создавая направленные магнитные силы, способствующие безконтактному удержанию и стабилизации объектов. Принцип работы основан на взаимодействии индуцированных токов с внешним магнитным полем, что позволяет генерировать подъемную силу, компенсирующую гравитацию.

При движении токопроводящих элементов в магнитном поле возникают вихревые токи (токи Фуко), на которые сила Лоренца оказывает воздействие, создавая противодействующую силу. В магнитолевитационных системах эту силу используют для создания устойчивого положения подвижных частей, например, в магнитных подшипниках и скоростных транспортных системах (маглев).

Точная настройка величины и направления магнитного поля обеспечивает контроль параметров силы Лоренца, что позволяет оптимизировать эффективную подъемную силу и уменьшить энергетические потери. Для максимальной эффективности важно минимизировать сопротивление проводников и обеспечить стабильность магнитного поля, так как сила Лоренца пропорциональна векторному произведению скорости носителей заряда и магнитной индукции.

В системах с переменным током и динамическими режимами работы важна синхронизация изменения магнитного поля с движением токопроводящих частей для предотвращения колебаний и резонансных эффектов. Практические решения включают использование сверхпроводящих магнитов и оптимизированных конфигураций катушек, что повышает силу Лоренца и снижает тепловые потери.

Таким образом, сила Лоренца является ключевым фактором, позволяющим преобразовать электрическую энергию в управляемую магнитную силу, обеспечивающую надежную и точную левитацию с минимальным трением и износом компонентов систем.

Движение капель электропроводящей жидкости в магнитогидродинамических установках

Капли электропроводящей жидкости в магнитогидродинамических (МГД) установках испытывают действие силы Лоренца, которая возникает при взаимодействии электрического тока внутри жидкости с внешним магнитным полем. При заданной плотности тока j и магнитной индукции B сила Лоренца F = j × B действует перпендикулярно направлению тока и магнитного поля, формируя направление движения капель.

Для капель диаметром порядка 10–100 мкм, движущихся в жидкостях с электропроводностью σ от 10³ до 10⁵ См/м, магнитное поле порядка 0,5–2 Тл способно существенно изменять траекторию движения. Скорость капель определяется балансом сил Лоренца, гидродинамического сопротивления и гравитации.

Практическое управление движением капель достигается изменением ориентации и величины магнитного поля, а также регулируемой величиной электрического тока. Это позволяет в МГД камерах контролировать направление и скорость капель, повышая эффективность процессов перемешивания, охлаждения или электролиза.

Особенностью движения капель в МГД установках является возникновение вихревых структур и индукционных токов в капле, что влияет на распределение напряжённостей внутри жидкости и может вызывать деформацию капель. Для предотвращения дестабилизации капель рекомендуется поддерживать магнитное поле в диапазоне, где магнитное давление не превышает поверхностное натяжение капли.

Оптимизация условий движения капель требует учёта параметров жидкости: вязкости, плотности, электропроводности, а также геометрии установки и характера внешнего поля. Экспериментальные данные подтверждают, что при увеличении магнитного числа М (отношение магнитных сил к гидродинамическим) выше 1 происходит устойчивое отклонение траекторий капель без разрушения их структуры.

Воздействие силы Лоренца на токи в рельсотроне и ускорение снаряда

При протекании электрического тока по двум параллельным токопроводящим рельсам создаётся магнитное поле, направленное вокруг каждого рельса по правилу правой руки. Снаряд, замыкающий цепь между рельсами, становится проводником с током, который испытывает силу Лоренца в магнитном поле рельс. Направление силы определяется правилом левой руки и ориентировано вдоль рельсов, толкая снаряд в сторону выхода.

Максимальная сила Лоренца F рассчитывается по формуле F = I × L × B, где I – сила тока в амперах, L – длина контактной части снаряда в метрах, B – магнитная индукция в теслах. Для достижения высоких значений F необходимы токи порядка десятков и сотен килоампер и магнитное поле выше 1 Тл.

Ускорение снаряда a определяется из второго закона Ньютона a = F / m, где m – масса снаряда. При массе снаряда порядка 0,1–1 кг и силе Лоренца 10^3–10^4 Н ускорение достигает 10^4–10^5 м/с², что обеспечивает выходную скорость снаряда свыше 2 км/с за доли секунды.

Для снижения потерь и повышения эффективности ускорения критически важно минимизировать сопротивление контакта между снарядом и рельсами, а также обеспечивать стабильный ток через весь ход снаряда. Применение сверхпроводящих рельсов и систем охлаждения позволяет увеличить максимальный ток и магнитное поле, усиливая силу Лоренца.

Динамическая устойчивость снаряда зависит от равномерности магнитного поля и симметрии токовых цепей. Неравномерности приводят к боковым силам и вибрациям, что ухудшает точность и ускорение. Контроль распределения токов и магнитного поля обязателен для оптимизации работы рельсотрона.

Вопрос-ответ:

Как сила Лоренца влияет на движение заряженной частицы в магнитном поле?

Сила Лоренца действует на заряженную частицу перпендикулярно как к её скорости, так и к магнитному полю. В результате частица движется по криволинейной траектории — обычно по окружности или спирали, если присутствует также электрическое поле. При этом сила не изменяет скорость частицы, а лишь меняет направление её движения. Такой эффект используется, например, в циклотроне и других типах ускорителей частиц.

Почему в рельсотроне токи под действием силы Лоренца способствуют ускорению снаряда?

В рельсотроне сила Лоренца возникает на ток, протекающий по двум параллельным проводникам — рельсам, и создаёт мощное магнитное поле между ними. Ток, проходящий через снаряд, взаимодействует с этим магнитным полем, вызывая силу, которая толкает снаряд вдоль рельс. Таким образом, снаряд ускоряется, превращая электрическую энергию в кинетическую. Это позволяет достичь очень высоких скоростей без использования химического топлива.

Как сила Лоренца проявляется в работе магнитной левитации (маглев)?

В системах магнитной левитации сила Лоренца создаёт подъемную и направляющую силы на токи, наведённые в проводящих элементах рельсов или вагона. При движении магнитного поля относительно проводников возникает индуцированный ток, и взаимодействие этого тока с магнитным полем генерирует силу, которая поднимает поезд над рельсами и стабилизирует его положение, уменьшая трение и позволяя развивать высокие скорости с плавным ходом.

В каких физических приборах используется эффект силы Лоренца для измерения магнитного поля?

Сила Лоренца применяется в магнитометрах, где токопроводящие пластины или провода помещают в изучаемое магнитное поле. Под действием силы Лоренца происходит отклонение токов или изменение их распределения, что регистрируется и преобразуется в показания о величине и направлении магнитного поля. Такие приборы широко используются для геофизических исследований, контроля качества материалов и в научных экспериментах.

Почему сила Лоренца не совершает работу над заряженной частицей в магнитном поле?

Сила Лоренца всегда направлена перпендикулярно к скорости частицы, поэтому не изменяет её кинетическую энергию — не увеличивает и не уменьшает скорость. Она лишь изменяет направление движения, заставляя частицу двигаться по изогнутой траектории. Работа силы равна произведению силы на перемещение в направлении силы, а так как здесь угол между силой и перемещением равен 90°, работа равна нулю.

Как сила Лоренца влияет на движение заряженных частиц в магнитном поле?

Сила Лоренца изменяет траекторию заряженных частиц, отклоняя их движение под углом к магнитному полю. Она действует перпендикулярно скорости частицы и направлению магнитного поля, заставляя частицы двигаться по круговой или спиральной траектории. Это явление используется, например, в ускорителях частиц для управления пучками и в анализаторах масс для разделения ионов по массе.