Как построить прямой угол с помощью циркуля

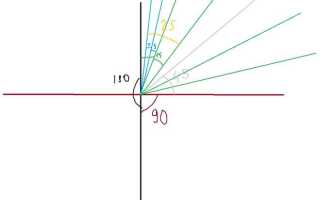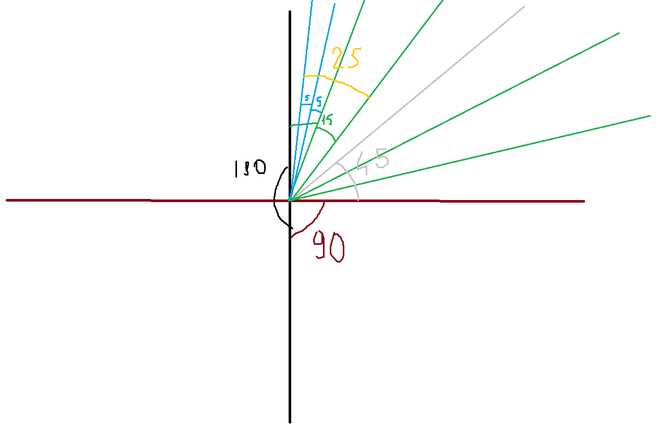
Построить прямой угол, используя только циркуль и без применения линейки, возможно благодаря свойствам окружности и точной геометрической последовательности. Этот метод опирается на построение равностороннего треугольника и биссектрис, которые образуют углы в 60° и 30°, позволяя получить угол в 90°.

Для построения требуется точка на плоскости, от которой проводится окружность произвольного радиуса. Затем, с помощью последовательных пересечений дуг, определяются опорные точки, позволяющие точно задать направления, между которыми формируется прямой угол. Все шаги выполняются только циркулем, без помощи прямых линий.

Подобный способ особенно полезен при ограниченных инструментах или в задачах, где запрещено использование линейки. Методика актуальна для изучения свойств геометрических построений, демонстрации точности классических инструментов и развития пространственного мышления.

Как начертить произвольную прямую с помощью только циркуля

Для построения произвольной прямой без линейки требуется определить два точки, через которые она пройдет. Это возможно при помощи окружностей, пересекающихся в двух местах. Порядок действий следующий:

1. Выбрать произвольную точку A на листе бумаги. Это будет первая точка прямой.
2. Установить произвольный радиус циркуля и начертить окружность с центром в точке A.
3. На окружности выбрать любую точку B. Это вторая точка, через которую пройдет прямая.
4. С тем же радиусом начертить окружность с центром в точке B. Она должна пересекаться с первой окружностью.
5. Отметить точки пересечения двух окружностей – назовем их C и D. Они лежат по разные стороны от отрезка AB.
6. Построить окружности с центрами в точках C и D и одинаковым радиусом, превышающим половину расстояния между C и D. Их пересечения обозначим как E и F.
7. Через точки E и F провести воображаемую линию – это и будет искомая прямая, проходящая через точки A и B.

Таким образом, прямую можно определить по двум точкам, полученным в результате пересечения окружностей. Эта методика позволяет выполнять построения без использования линейки, опираясь только на свойства равных радиусов и симметрии.

Построение равных отрезков на дуге окружности

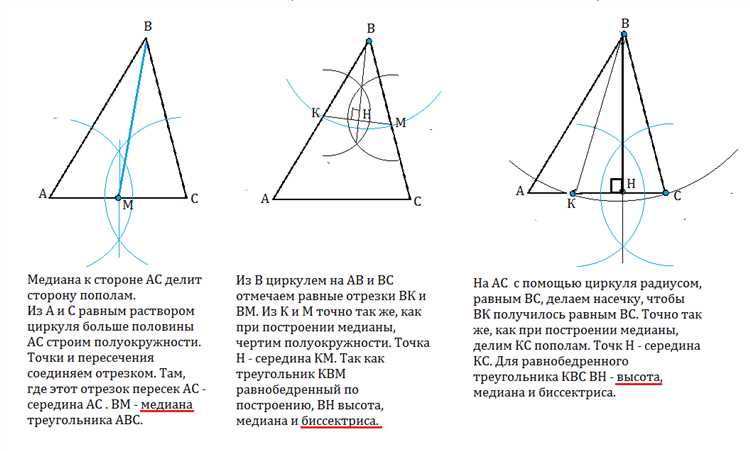
Для деления дуги окружности на равные части с помощью циркуля потребуется зафиксировать один радиус в качестве начального и отложить на дуге равные хорды. Процесс начинается с построения окружности произвольного радиуса и обозначения на ней начальной точки A.

Циркулем измеряется радиус окружности, затем его величина уменьшается до желаемой длины хорды – она определяет длину каждого отрезка. Циркуль устанавливается в точку A, отсекается первая дуга, отмечается точка B. Затем, не меняя радиуса, с точки B отсекается следующая дуга – точка C, и так далее, пока не получится нужное количество равных дуг.

Если требуется, например, разделить дугу на 6 равных отрезков, длину дуги можно подобрать экспериментально, добиваясь, чтобы при последовательных отсечениях последняя точка совпала с конечной точкой всей дуги. При несовпадении радиус корректируется, и процедура повторяется.

Для точности желательно использовать остро заточенный грифель и прочную фиксацию ножки циркуля. Ошибки в измерении радиуса приведут к накоплению погрешности, особенно при большом числе делений. При необходимости можно использовать вспомогательную окружность того же радиуса, чтобы заранее проверить количество укладываемых отрезков.

Пошаговое деление дуги пополам без линейки

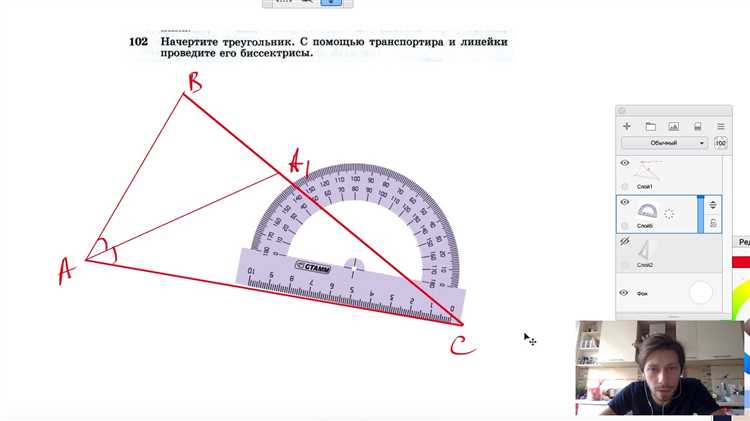
1. Установить ножку циркуля в точку A – одну из концов дуги.

2. Провести дугу, пересекающую исходную дугу с внутренней стороны, не изменяя радиус.

3. Не меняя раскрытие, установить циркуль в точку B – вторую конечную точку дуги.

4. Провести вторую дугу, также пересекающую исходную дугу. Обе новые дуги должны пересечься в одной точке внутри исходной дуги.

5. Образовавшаяся точка пересечения обозначает вершину равнобедренного треугольника с основанием AB.

6. Соединить эту точку с центром исходной дуги (если он известен), либо воспользоваться симметрией: установить циркуль в точку пересечения, провести две дуги, пересекающие дугу снаружи, и определить среднюю точку дуги по пересечению дополнительных дуг.

7. Полученная точка на исходной дуге делит её на две равные части без применения линейки.

Построение перпендикуляра к отрезку через заданную точку

Для построения перпендикуляра к отрезку, проходящего через заданную точку, потребуется циркуль. Линейка не используется. Рассматриваются два случая: точка лежит на отрезке и вне его.

• Если точка лежит на отрезке:

  1. С установкой иглы циркуля в заданную точку, провести дугу, пересекающую отрезок в двух точках по обе стороны от заданной точки.
  2. С тем же радиусом, поставить иглу циркуля в каждую из точек пересечения и провести две дуги, чтобы они пересеклись между собой по обе стороны от отрезка.
  3. Соединить точку пересечения дуг с заданной точкой. Полученная прямая – перпендикуляр.

• Если точка вне отрезка:

  1. Поставить иглу циркуля в заданную точку и провести дугу, пересекающую отрезок в двух точках.
  2. Сохранить радиус. Поставить иглу в одну из точек пересечения и провести дугу ниже отрезка. Повторить из второй точки пересечения.
  3. Соединить точку пересечения дуг с исходной точкой. Это и есть искомый перпендикуляр.

Радиус дуг должен быть выбран так, чтобы обеспечить пересечение. Не рекомендуется брать слишком малый радиус: дуги могут не пересечься или не достигнуть отрезка.

Как получить угол в 90 градусов на пересечении дуг

Для построения прямого угла без линейки используют пересечение дуг, проведённых циркулем. Начальная точка – вершина предполагаемого угла. Из неё проводят окружность произвольного радиуса. Она пересекает предполагаемую прямую в двух точках – A и B.

Из точек A и B тем же радиусом проводят две дуги. Они пересекаются выше или ниже прямой – в зависимости от положения циркуля – в точке C. Отрезок от центра окружности до точки C делит дугу пополам под углом 90 градусов относительно хорды AB.

Проверка: треугольник ACB – равнобедренный, а угол при вершине C – прямой, так как построен как пересечение двух равных дуг, образующих симметрию относительно отрезка AB.

Чтобы получить чёткий прямой угол, важно соблюдать одинаковый радиус при всех построениях и точно фиксировать точки пересечения. Малейшее отклонение приведёт к погрешности в угле.

Проверка прямого угла без угольника и линейки

Для проверки прямого угла без специальных инструментов достаточно использовать свойства окружности и циркуля. Если на угле провести дугу с центром в вершине угла, то на концах пересечения дуги с сторонами угла необходимо отметить точки. Соединив эти точки отрезком, нужно построить еще одну дугу с тем же радиусом и центром в одной из отмеченных точек.

Если отрезок, соединяющий две точки пересечения дуг, совпадает по длине с радиусом, а точка пересечения второй дуги с другой стороной угла совпадает с ранее отмеченной, угол равен 90°.

Альтернативно можно применить треугольник с соотношением сторон 3:4:5. Измерив от вершины угла по каждой стороне отрезки длиной 3 и 4 единицы (отметив циркулем), и проверив расстояние между этими отметками равным 5, определяют прямой угол.

Точность проверки зависит от аккуратности построений и выбранного радиуса. Лучше выбирать радиус, не слишком малый, чтобы минимизировать погрешности.

Использование этих методов позволяет определить прямой угол без угольника и линейки с погрешностью, достаточной для большинства практических задач.

Вопрос-ответ:

Как можно построить прямой угол только с помощью циркуля, без использования линейки?

Для построения прямого угла с помощью циркуля нужно начертить окружность с центром в точке вершины угла, после чего на пересечении окружности с одной из сторон угла построить две одинаковые дуги, которые пересекутся внутри окружности. Соединение вершины угла с точкой пересечения этих дуг даст прямой угол. Этот способ основан на свойствах равнобедренных треугольников и равенства дуг.

Почему линейка не нужна при построении прямого угла таким способом?

Линейка обычно используется для проведения прямых линий, но в данном методе важна точность равенства отрезков и дуг, которые создаёт циркуль. Благодаря свойствам окружностей и равных дуг можно обойтись без измерения длины с помощью линейки. Циркуль позволяет задать одинаковый радиус и таким образом строить равные отрезки, что помогает создать прямой угол без дополнительного инструмента.

Какие ошибки часто встречаются при построении прямого угла циркулем и как их избежать?

Наиболее частые ошибки связаны с неправильным выбором радиуса циркуля и неточным нанесением точек пересечения дуг. Если радиус слишком мал или слишком велик, точки могут не пересечься или построенный угол будет искажен. Чтобы избежать ошибок, следует внимательно устанавливать радиус и аккуратно ставить точки, используя чёткие и точные движения. Также важно проверить построение, чтобы убедиться, что все линии и дуги соответствуют правилам.

Можно ли этот способ использовать для построения прямого угла на бумаге с неровной поверхностью или на других материалах?

Принцип построения сохраняется на любой поверхности, где можно точно поставить точки и провести линии циркулем. Однако на неровной или мягкой поверхности точность снижается, поскольку циркуль может скользить или точка установки может смещаться. Для таких случаев рекомендуется использовать твёрдую и ровную основу, чтобы линии были точными и четкими.

Какую практическую пользу имеет построение прямого угла без линейки? В каких ситуациях это может пригодиться?

Этот способ полезен, когда под рукой нет линейки, а необходимо быстро и точно построить прямой угол, например, в полевых условиях, при работе с деревянными деталями или на строительстве. Кроме того, такой метод помогает лучше понять геометрические свойства фигур и развить навыки работы с циркулем. Он также подходит для обучения основам геометрии и развития пространственного мышления.

Как с помощью циркуля можно построить прямой угол без использования линейки?

Для построения прямого угла циркулем без линейки нужно выполнить несколько последовательных действий. Сначала ставят точку — вершину угла. Затем из этой точки проводят дугу окружности произвольного радиуса, чтобы получить две точки пересечения с будущими сторонами угла. Далее из каждой из этих точек проводят дуги с одинаковым радиусом, которые пересекутся между собой. Соединив точку вершины с точкой пересечения этих дуг, получают линию, образующую прямой угол с первой стороной. Таким образом, получается угол 90 градусов, не используя прямых измерительных инструментов, кроме циркуля.

Почему при построении прямого угла циркулем без линейки важно выбирать одинаковый радиус для дуг, и как это влияет на точность?

При построении прямого угла одинаковый радиус для дуг, проведённых из точек пересечения с начальной дугой, необходим для того, чтобы пересечение этих дуг оказалось симметричным относительно исходной линии. Если радиусы будут разными, точка пересечения сместится, и линия, проведённая через вершину угла и эту точку, не будет перпендикулярна исходной стороне. Таким образом, одинаковый радиус гарантирует равные расстояния от точек дуг до точки пересечения, что обеспечивает правильное расположение второй стороны угла и, следовательно, точность построения именно прямого угла.