Что такое резонанс в электрической цепи

Резонанс в электрической цепи возникает при совпадении частоты внешнего источника с собственной частотой колебательного контура. В этом режиме реактивные сопротивления индуктивности и ёмкости компенсируют друг друга, что приводит к резкому изменению амплитудных характеристик тока и напряжения. Такое явление наблюдается как в последовательных, так и в параллельных цепях переменного тока.

В последовательной RLC-цепи при резонансе суммарное сопротивление достигает минимального значения и равно активному сопротивлению контура. Ток при этом максимален, а фаза между током и напряжением стремится к нулю. Для расчёта резонансной частоты используется формула: f₀ = 1 / (2π√(LC)), где L – индуктивность, C – ёмкость.

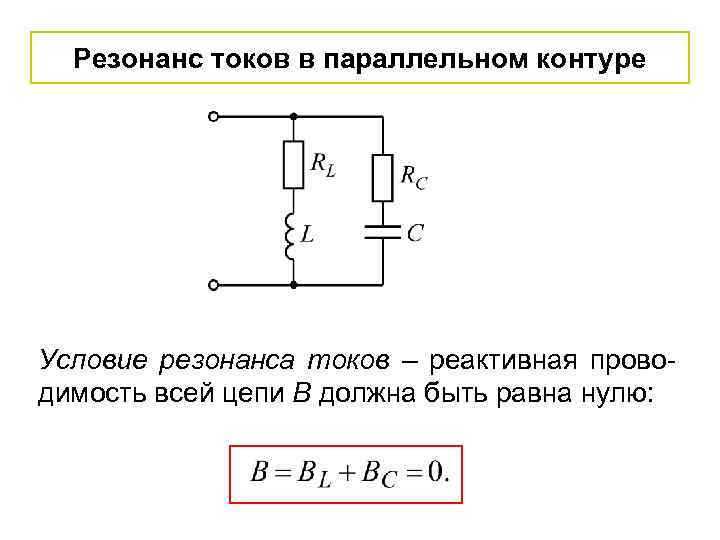
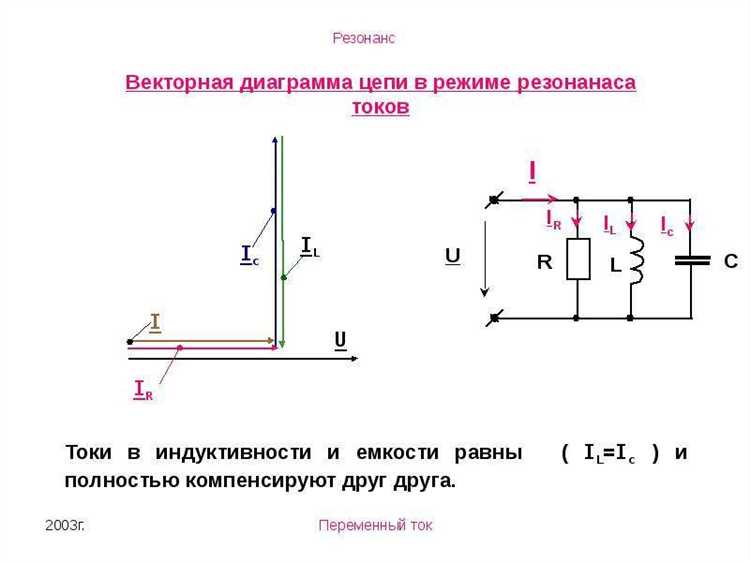
В параллельной цепи резонанс приводит к минимальному току из сети, хотя в ветвях LC может возникать значительная циркулирующая мощность. Такой эффект особенно важен при проектировании фильтров, согласующих устройств и схем с усилением на определённой частоте.

Наличие активного сопротивления вызывает затухание, которое характеризуется добротностью Q. Чем выше Q, тем более выражен резонансный пик, и тем уже резонансная кривая. При выборе параметров цепи важно учитывать требования к стабильности, потере энергии и допустимому отклонению частоты.

Понимание особенностей резонансных процессов позволяет точно настраивать устройства радиосвязи, фильтрации сигналов, импульсной техники и импедансного согласования. Пренебрежение влиянием резонанса может привести к перегреву компонентов, искажению сигналов или потере эффективности.

Условия возникновения резонанса в колебательном контуре

Резонанс в колебательном контуре возникает тогда, когда частота внешнего воздействия совпадает с собственной частотой колебаний контура. Для идеального последовательного колебательного контура, состоящего из катушки индуктивности и конденсатора, собственная резонансная частота определяется выражением: \( f_0 = \frac{1}{2\pi\sqrt{LC}} \), где \( L \) – индуктивность в генри, \( C \) – ёмкость в фарадах.

Одним из ключевых условий резонанса является минимальное значение активного сопротивления цепи. Чем ниже сопротивление, тем выше добротность и выраженнее резонансный эффект. При этом в резонансной точке полное сопротивление последовательного контура становится минимальным, так как реактивные сопротивления индуктивности и ёмкости компенсируют друг друга: \( X_L = X_C \).

В параллельном колебательном контуре резонанс наступает при условии равенства модулей индуктивного и ёмкостного сопротивлений, но ток через источник в этот момент минимален, а напряжение на реактивных элементах может многократно превышать входное. Это используется в фильтрах и согласующих цепях, где важна селективность по частоте.

Наличие паразитных сопротивлений и потерь в элементах приводит к смещению резонансной частоты и снижению амплитуды резонансного отклика. Поэтому при расчётах следует учитывать реальное значение добротности: \( Q = \frac{1}{R}\sqrt{\frac{L}{C}} \) для последовательного контура, где \( R \) – эквивалентное сопротивление.

Для точной настройки резонансной частоты рекомендуется использовать прецизионные компоненты и учитывать температурные зависимости параметров. Особенно важно это в высокочастотных схемах, где даже незначительное отклонение параметров влияет на режим резонанса.

Как влияет резонанс на напряжение и ток в цепи

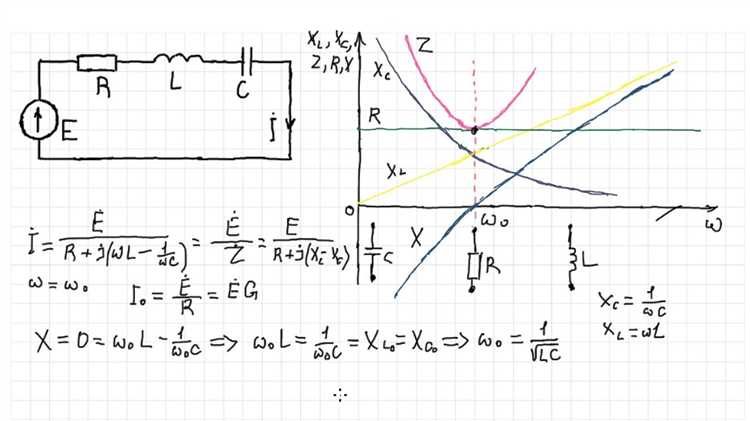
При возникновении резонанса в колебательном контуре переменного тока полное сопротивление цепи минимизируется и становится равным активному сопротивлению. Это происходит при условии, что индуктивное и емкостное сопротивления уравновешиваются: \(X_L = X_C\), где \(X_L = \omega L\), \(X_C = 1/\omega C\), а \(\omega\) – круговая частота.

В этом состоянии ток в цепи достигает максимального значения, определяемого как \(I = U/R\), где \(U\) – амплитуда приложенного напряжения, \(R\) – активное сопротивление. Даже при небольшом напряжении ток может быть значительно выше среднего, особенно при малых значениях \(R\).

Напряжения на катушке индуктивности и конденсаторе при резонансе превышают входное напряжение. Это связано с тем, что при высокой добротности контура ток остаётся большим, а реактивные сопротивления элементов тоже велики. Таким образом, \(U_L = I \cdot X_L\) и \(U_C = I \cdot X_C\) могут быть в десятки раз выше входного напряжения, несмотря на то, что их алгебраическая сумма равна нулю.

Повышенное напряжение на реактивных элементах требует тщательного выбора номиналов и изоляции, особенно в устройствах с высокой добротностью. Например, при добротности \(Q = 50\) и напряжении источника 10 В, амплитуда напряжения на катушке может достигать 500 В. Игнорирование этого факта приводит к пробою диэлектриков и выходу элементов из строя.

В практических приложениях, таких как радиопередатчики и фильтры, резонанс используется для усиления сигналов в узком диапазоне частот. Однако в силовых цепях его влияние может быть разрушительным, если не предусмотрены меры по ограничению токов и напряжений.

Расчёт резонансной частоты для RLC-цепей

Резонансная частота в последовательной или параллельной RLC-цепи определяется на основании индуктивного и ёмкостного сопротивлений. При резонансе реактивные сопротивления индуктивности и ёмкости компенсируют друг друга, и результирующее сопротивление цепи зависит только от активного сопротивления R.

Формула расчёта резонансной частоты \( f_0 \) для идеальной последовательной RLC-цепи:

f₀ = 1 / (2π√(LC))

Здесь:

L – индуктивность в генри (Гн),

C – ёмкость в фарадах (Ф),

π ≈ 3,1416.

Например, если L = 10 мГн (0,01 Гн), а C = 1 мкФ (1×10⁻⁶ Ф), то резонансная частота будет:

f₀ = 1 / (2 × 3,1416 × √(0,01 × 1×10⁻⁶)) ≈ 1591,55 Гц

Для параллельной RLC-цепи с учётом потерь точная формула резонансной частоты отличается и включает влияние сопротивления R. При малых потерях используется приближённая формула, аналогичная последовательной цепи:

f₀ ≈ 1 / (2π√(LC))

Если сопротивление велико, для точного расчёта параллельного резонанса применяется уточнённая формула:

f₀ = 1 / (2π) × √(1/LC − (R² / L²))

Эта формула показывает, что при увеличении R резонансная частота снижается. При расчётах важно следить за размерностями величин: если L задаётся в миллигенри, а C – в микрофарадах, необходимо переводить их в генри и фарады соответственно.

Для практических целей рекомендуется использовать частотный диапазон, в котором f₀ попадает в рабочую область прибора или схемы. При проектировании также учитывается добротность, которая зависит от соотношения L, C и R, и влияет на крутизну резонансного пика.

Влияние сопротивления на форму резонансной кривой

Форма резонансной кривой в RLC-цепи напрямую зависит от величины активного сопротивления, входящего в контур. При фиксированных значениях индуктивности и емкости, сопротивление определяет добротность цепи и влияет на ширину полосы пропускания.

При низком сопротивлении (высокая добротность):

Резонансная кривая имеет узкий пик вблизи резонансной частоты.
Максимум амплитуды тока достигается при минимальном рассеянии энергии.
Цепь становится избирательной к частоте, реагируя в основном на сигнал с частотой, близкой к резонансной.

При увеличении сопротивления (снижение добротности):

Пик на резонансной кривой становится более пологим.
Ширина полосы пропускания возрастает, что уменьшает частотную избирательность цепи.
Максимальное значение тока в резонансе уменьшается.

Добротность можно выразить как:

Q = (1/R)·√(L/C)

где R – активное сопротивление, L – индуктивность, C – емкость.

При проектировании контуров, где требуется высокая селективность (например, в радиоприеме), используют минимально возможное сопротивление. В других случаях, где важна стабильность и подавление паразитных колебаний, допустимо большее значение R для сглаживания резонансной кривой.

Примеры применения резонансных явлений в радиотехнике

Резонанс в радиотехнических цепях широко применяется для выделения и обработки сигналов с заданной частотой. Ниже приведены ключевые примеры:

Настройка радиоприёмников. Колебательные контуры с резонансной частотой служат для селекции радиостанций, выделяя нужный сигнал и подавляя остальные. Частотная настройка достигается изменением ёмкости или индуктивности контура.
Фильтры полосы пропускания. Резонансные цепи применяются в полосовых и режекторных фильтрах для подавления нежелательных частот и повышения качества сигнала.
Генераторы колебаний. В схеме генератора резонансный контур определяет стабильность и частоту генерируемых сигналов, что важно в радиостанциях и передающих устройствах.
Антенны с согласованием по резонансу. Антенны проектируют так, чтобы их собственная резонансная частота совпадала с частотой передаваемого или принимаемого сигнала, что улучшает КПД передачи и приёма.
Импульсные и частотные модуляторы. Резонансные цепи используются для формирования и выделения узкополосных сигналов с требуемыми характеристиками.

При проектировании радиотехнических устройств важно учитывать добротность резонансного контура. Высокое значение добротности обеспечивает узкую резонансную полосу и повышенную избирательность, но требует точной настройки и контроля параметров цепи.

Резонансные явления также находят применение в системах автоматической подстройки частоты (АПЧ), где сигнал с определённой частотой стабилизируется за счёт обратной связи с резонансным контуром.

Опасности и перегрузки при резонансе в бытовых устройствах

Резонанс в электрических цепях бытовых приборов может приводить к значительному повышению амплитуды напряжения и тока, что создает риск выхода из строя компонентов. В цепях с индуктивностью и емкостью при совпадении частоты питающего сигнала с резонансной происходит резкое снижение полного сопротивления, что ведет к перегрузке элементов и повышенному тепловыделению.

Перегрузка обмоток электродвигателей и трансформаторов часто связана с резонансными режимами. При этом наводятся большие токи, превышающие номинальные значения, что ускоряет износ изоляции и приводит к коротким замыканиям. Также возможны повреждения конденсаторов из-за перенапряжений, вызванных резонансом.

Для снижения рисков рекомендуется использовать устройства защиты от перегрузок и перенапряжений, а также предусматривать демпфирующие элементы – резисторы или активные фильтры, снижающие добротность контура. В современных бытовых приборах часто применяют схемы с плавным запуском и ограничением тока, предотвращающие резонансные скачки.

Регулярное техническое обслуживание и проверка электросетей позволяют выявить и устранить условия, приводящие к резонансу. В частности, важно избегать нецелевого включения конденсаторов параллельно с индуктивными нагрузками без расчёта резонансной частоты, что снижает вероятность возникновения опасных режимов.

Незначительное смещение частоты питающей сети от резонансной существенно уменьшает нагрузку на цепь, поэтому рекомендуется контролировать стабильность питающего напряжения и частоты. При проектировании бытовых устройств важно учитывать потенциальные резонансные точки и обеспечивать запас по току и напряжению для безопасной эксплуатации.

Методы настройки цепи на резонансную частоту

Настройка цепи на резонансную частоту требует точного определения параметров индуктивности и емкости. Основной метод заключается в подборе значения конденсатора или катушки индуктивности для выполнения условия резонанса: ω₀ = 1/√(LC), где ω₀ – резонансная циклическая частота.

Часто применяется варикап – изменяемый емкостной элемент, который позволяет плавно регулировать емкость в диапазоне, обеспечивающем достижение резонанса без механической замены компонентов. В радиотехнических схемах варикап подключается параллельно катушке или последовательно с ней для точной подстройки.

Для более грубой настройки используется переключение конденсаторов или катушек с разными номиналами. Такой метод удобен при прототипировании или когда требуется фиксированное значение резонансной частоты.

Измерение резонансной частоты проводят при помощи частотомера или анализатора спектра, регистрируя максимальное значение напряжения или тока в цепи. Настройка осуществляется до достижения пика в амплитудно-частотной характеристике.

Для автоматической подстройки применяют схемы с фазовым детектором и контуром обратной связи, поддерживающим постоянный резонанс при изменении параметров цепи или внешних условий.

Важным моментом является контроль потерь и сопротивления, поскольку они влияют на ширину резонансной кривой и точность настройки. Оптимальный выбор элементов и их параметров обеспечивает стабильность резонанса и снижает искажения сигнала.

Вопрос-ответ:

Что такое резонанс в электрической цепи и как он возникает?

Резонанс в электрической цепи — это явление, при котором реактивные сопротивления конденсатора и катушки взаимно компенсируются на определённой частоте. На этой резонансной частоте общее реактивное сопротивление цепи стремится к нулю, а ток достигает максимального значения. Возникает это из-за совпадения частоты питающего сигнала с собственной частотой колебательного контура, образованного индуктивностью и ёмкостью.

Как резонанс влияет на напряжение и ток в цепи?

При резонансе напряжение на индуктивном и ёмкостном элементах может значительно превышать приложенное к цепи напряжение, поскольку их реактивные сопротивления по модулю равны, но противоположны по фазе. В результате амплитуда тока достигает максимума, а сопротивление цепи минимально. Это приводит к увеличению мощности в контуре и повышенному нагреву элементов, что требует контроля для предотвращения повреждений.

Какие параметры цепи влияют на резонансную частоту?

Резонансная частота определяется значениями индуктивности (L) и ёмкости (C) в цепи и рассчитывается по формуле f₀ = 1 / (2π√(LC)). Сопротивление влияет на добротность контура, но не изменяет основную резонансную частоту. Изменение L или C приводит к смещению резонансной частоты, что позволяет настроить цепь на нужный режим работы.

Как избежать перегрузок и повреждений в цепи при резонансе?

Для предотвращения перегрузок применяют ограничение тока с помощью сопротивлений или предохранителей, используют цепи с умеренной добротностью, что снижает резонансные пики. Кроме того, контролируют параметры элементов и обеспечивают охлаждение. В некоторых случаях используют активное управление частотой или фазой сигнала для обхода опасных резонансных режимов.

В каких практических устройствах используется резонанс в электрических цепях?

Резонанс применяется в радиоприёмниках и передатчиках для настройки на определённые частоты сигнала, в фильтрах для выделения узкополосных частот, в индукционных нагревателях для эффективной передачи энергии, а также в системах передачи переменного тока для компенсации реактивной мощности и повышения коэффициента мощности. Это позволяет повысить точность и экономичность работы оборудования.

Что происходит с током и напряжением в цепи при наступлении резонанса?

При резонансе индуктивное и ёмкостное сопротивления в цепи равны по величине, но противоположны по фазе, поэтому взаимно компенсируются. В результате общий реактивный импеданс минимален, и цепь ведёт себя почти как чисто активная. Это приводит к максимальному значению тока в цепи, при этом напряжение на отдельных элементах — катушке и конденсаторе — может значительно превышать напряжение источника из-за резонансного повышения. Такое явление называют резонансным усилением напряжения и тока.

Какие факторы влияют на точность настройки резонансной частоты в электрической цепи?

Основные факторы — параметры элементов цепи: индуктивность катушки, ёмкость конденсатора и сопротивление проводников и нагрузки. Изменения этих параметров под воздействием температуры, частоты, качества материалов и износа влияют на резонансную частоту. Кроме того, наличие паразитных ёмкостей и индуктивностей, а также точность измерений вносят отклонения. Для точной настройки применяют подстроечные элементы и контролируют условия работы, чтобы сохранить стабильность частоты.