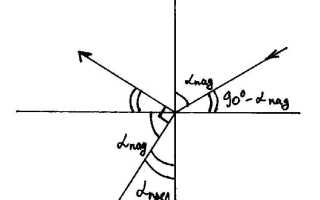Как изменится угол между падающим и отраженным лучами света

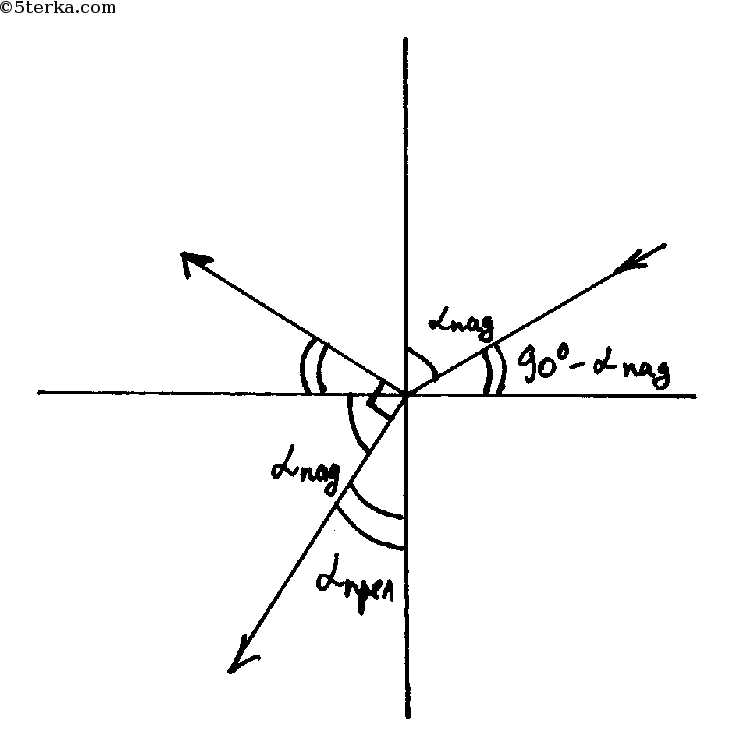
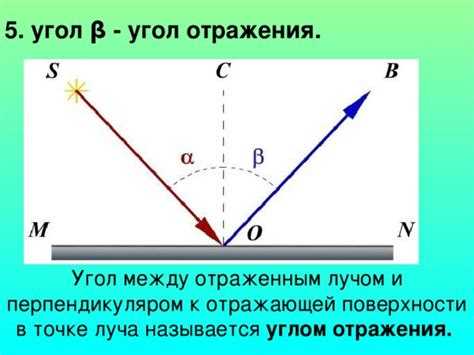
Угол между падающим и отражённым лучами в классической геометрической оптике не изменяется: он всегда равен удвоенному углу падения. Это следует из закона отражения, согласно которому угол падения равен углу отражения относительно нормали к поверхности.

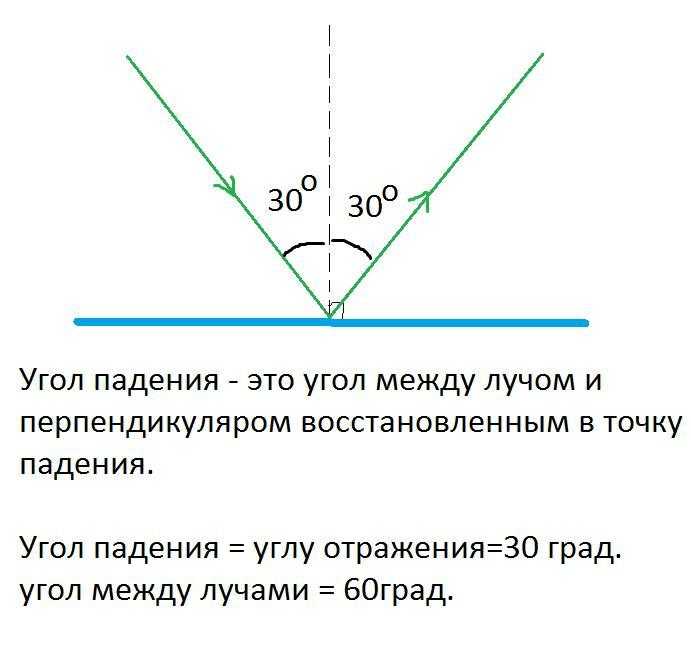
При изменении угла падения, например, с 20° до 40°, угол между лучами возрастает с 40° до 80°. Это линейная зависимость: угол между лучами = 2 × угол падения. При угле падения 0° (луч перпендикулярен поверхности) отражённый луч идёт по тому же пути, и угол между лучами равен 0°.

Если поверхность не идеально гладкая, а диффузная, отражение становится рассеянным, и прямой зависимости между углом падения и углом отражения нет. В таких случаях для расчётов используют модели вроде закона Ламберта или отражения Бидиракционного распределения отражательной способности (BRDF).

При переходе между средами с разной оптической плотностью (например, воздух–стекло) возникает частичное отражение с поверхности. Угол между падающим и отражённым лучами всё равно подчиняется закону отражения, но интенсивность отражённого луча зависит от угла падения и поляризации света. На границе воздух–стекло при угле Брюстера (около 56° для красного света) отражённый луч полностью поляризован в плоскости, перпендикулярной плоскости падения.

Как определить угол падения и угол отражения на плоской поверхности

Угол отражения – это угол между нормалью и направлением отражённого луча. По закону отражения: угол отражения всегда равен углу падения. Это позволяет проверять точность построения – если отражённый луч не симметричен относительно нормали, значит, допущена ошибка в построении или измерении.

Для практического измерения используют лазерный луч, плоское зеркало и экран. Отметив точки входа и выхода луча, соединяют их с точкой падения. Построив нормаль, определяют углы с помощью геометрического построения или измерительного инструмента.

Угол всегда измеряется в плоскости падения – плоскости, содержащей и падающий, и отражённый луч. Если поверхность не идеально плоская, возникают отклонения, и закон отражения нарушается. Поэтому поверхность должна быть ровной, а точка падения – чётко определённой.

Что происходит с углами при изменении угла наклона зеркала

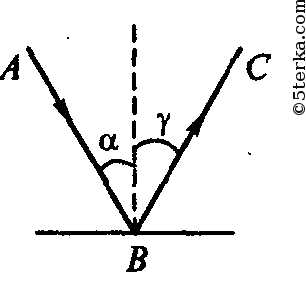
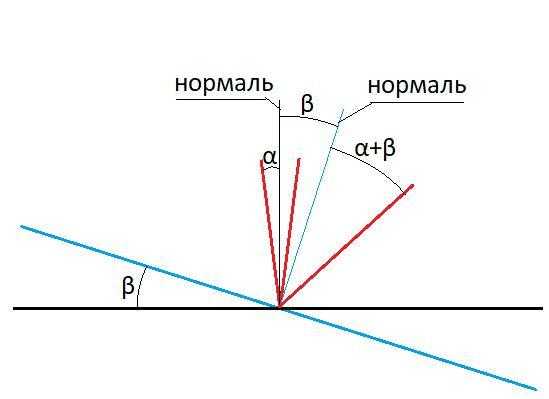
Если зеркало поворачивается на угол α относительно исходного положения, угол падения и угол отражения изменяются на тот же угол α. Это объясняется законом отражения: угол отражения всегда равен углу падения, считая оба от перпендикуляра к поверхности.

Например, если падающий луч сохраняет своё направление, а зеркало поворачивается на 10°, отражённый луч отклоняется на 20° от прежнего направления. Это удвоение вызвано тем, что изменение нормали приводит к симметричному изменению обоих углов относительно новой оси.

Рекомендация: при расчётах учитывать, что при неизменном направлении падающего луча, изменение угла наклона зеркала на α приводит к повороту отражённого луча на 2α. Это важно для настройки оптических систем, где требуются точные углы отклонения.

Если же меняется направление самого падающего луча при фиксированном зеркале, отражённый луч отклоняется симметрично. Но в случае вращения зеркала отражённый луч всегда реагирует в два раза сильнее по углу, чем само зеркало.

Изменяется ли угол между лучами при движении источника света

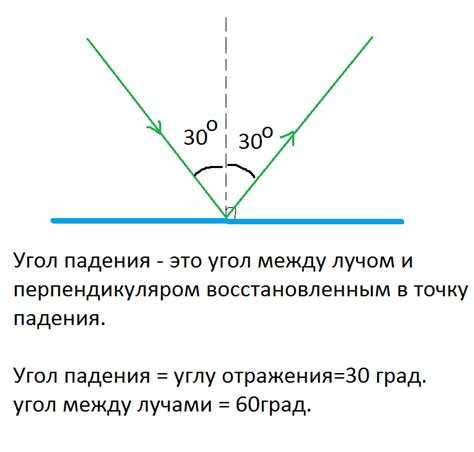
При движении источника света параллельно отражающей поверхности угол между падающим и отражённым лучами не изменяется. Это связано с тем, что закон отражения остаётся неизменным: угол падения равен углу отражения независимо от положения источника.

Если источник света движется перпендикулярно к поверхности, траектория луча изменяется, но геометрия отражения сохраняется. Направление падающего луча сдвигается, однако угол между падающим и отражённым лучами остаётся прежним, поскольку отражение происходит относительно нормали в точке падения.

Изменения наблюдаются только при наличии среды с переменными оптическими свойствами или при движении отражающей поверхности. В этом случае может возникать эффект Доплера или смещение фазы, но сам угол между падающим и отражённым лучами в рамках геометрической оптики остаётся постоянным.

Для точных измерений при высоких скоростях источника (порядка сотен тысяч км/ч) необходимо учитывать релятивистские эффекты. Однако в школьной и прикладной физике такие отклонения незначительны и пренебрежимо малы.

Как влияет кривизна отражающей поверхности на угол между лучами

При отражении от криволинейной поверхности угол между падающим и отражённым лучами зависит от местной нормали в точке контакта. В отличие от плоской поверхности, где нормаль постоянна, на кривой поверхности она меняется от точки к точке. Это приводит к изменению направления отражённого луча даже при постоянном направлении падающего.

Для вогнутых поверхностей (например, сферических зеркал) угол между лучами уменьшается по мере приближения точки падения к центру кривизны. Это связано с тем, что отражённые лучи стремятся к фокусу. Для выпуклых поверхностей угол, наоборот, увеличивается: отражённые лучи расходятся.

Величина изменения угла зависит от радиуса кривизны. Чем меньше радиус, тем сильнее отклоняется нормаль от вертикали при малом смещении точки падения, а значит, тем заметнее изменение направления отражения.

Рекомендуется учитывать следующее:

При проектировании оптических систем с кривыми зеркалами необходимо рассчитывать локальный угол падения относительно нормали в каждой точке.
Для точных измерений применять трассировку лучей с учётом формы поверхности, особенно при использовании параболических или гиперболических отражателей.
При анализе рассеяния следует учитывать, что на микронеровностях угол отражения может отличаться от геометрически ожидаемого.

Почему угол между падающим и отражённым лучами не всегда равен 180°

В идеальных условиях, при зеркальном отражении от гладкой поверхности, угол между падающим и отражённым лучами действительно составляет 180°, поскольку лучи лежат на одной прямой, и угол отражения равен углу падения. Однако на практике это условие нарушается при наличии неровностей на поверхности, неоднородности среды или при диффузном отражении.

Если поверхность шероховатая, каждый микроскопический участок отражает луч по-своему. Лучи после отражения расходятся в разных направлениях, и угол между падающим и каким-либо из отражённых лучей может быть меньше или больше 180°, в зависимости от характера рассеяния. Такое поведение типично, например, для матовых поверхностей, где формально нельзя определить единичный угол отражения.

При переходе луча через границу двух сред с различными показателями преломления (например, воздух – стекло), часть энергии отражается, а часть преломляется. В случае косого падения угол между падающим и отражённым лучами может отличаться от 180°, особенно если учитывать трёхмерное распределение лучей относительно нормали к поверхности.

Для точного анализа необходимо использовать векторное представление лучей и учитывать ориентацию отражающей поверхности. Даже при зеркальном отражении, если лучи не лежат в одной плоскости, проекция угла на плоскость наблюдения не даст 180°.

Чтобы минимизировать отклонения и получить угол, близкий к 180°, рекомендуется использовать плоские, полированные поверхности и соблюдать симметричное расположение источника и приёмника света относительно нормали к поверхности.

Примеры расчёта угла между лучами в разных оптических системах

Угол между падающим и отражённым лучами определяется законом отражения: угол падения равен углу отражения относительно нормали. Для разных систем расчёт имеет свои особенности.

Плоское зеркало:
1. Определите угол падения \(\theta_i\) – угол между падающим лучом и нормалью к поверхности.
2. Угол отражения \(\theta_r = \theta_i\).
3. Угол между падающим и отражённым лучами равен \(2\theta_i\).
Вогнутое сферическое зеркало:
1. Вычислите точку падения луча на зеркальную поверхность с учётом радиуса кривизны \(R\).
2. Нормаль к поверхности – радиус-вектор к точке падения.
3. Измерьте угол падения относительно нормали \(\theta_i\), затем угол отражения \(\theta_r = \theta_i\).
4. Угол между лучами равен \(2\theta_i\), но из-за кривизны искажён в пространстве, требуется учитывать координаты точек для точного направления.
Призма с преломлением и отражением:
1. Определите угол падения на грани призмы \(\theta_i\).
2. Используйте закон преломления (закон Снеллиуса) для расчёта угла преломлённого луча.
3. Если луч отражается внутри призмы, примените закон отражения для внутренней грани.
4. Угол между падающим и отражённым лучами на отражающей грани равен \(2\theta_i\), однако итоговый угол между исходным падающим и окончательно выходящим лучом нужно считать с учётом преломления и внутренних отражений.
Зеркальный угловой отражатель (например, отражатель типа «коровий глаз»):
1. Луч падает на две перпендикулярные зеркальные поверхности.
2. Сначала рассчитайте угол отражения на первой поверхности \(\theta_1 = \theta_i\).
3. Второе отражение происходит на другой поверхности под углом \(\theta_2\), равным углу падения на эту грань.
4. Итоговый угол между падающим и дважды отражённым лучом равен \(180^\circ\), то есть луч возвращается обратно параллельно падающему, что проверяется через векторный расчёт.

Рекомендации по точности расчётов:

При работе с криволинейными поверхностями учитывайте локальную нормаль в точке падения.
Для сложных систем используйте векторный анализ направления лучей, а не только углы относительно нормали.
Проверяйте результат с помощью геометрического моделирования, чтобы исключить ошибки, связанные с искажениями и преломлениями.

Вопрос-ответ:

Как определяется угол между падающим и отражённым лучами при отражении света?

Угол между падающим и отражённым лучами определяется исходя из закона отражения, согласно которому угол падения равен углу отражения. Поскольку оба угла измеряются относительно нормали к поверхности, угол между падающим и отражённым лучами всегда равен удвоенному углу падения. То есть, если угол падения равен α, то угол между лучами будет 2α.

Изменится ли угол между падающим и отражённым лучами, если изменить ориентацию отражающей поверхности?

Да, угол между падающим и отражённым лучами изменится, если наклонить отражающую поверхность. Поворот поверхности приводит к изменению нормали, относительно которой измеряются углы. Это повлияет на угол падения и, соответственно, на угол отражения. Поскольку угол между лучами равен удвоенному углу падения, изменение ориентации поверхности напрямую меняет этот угол.

Как влияет изменение угла падения на угол между падающим и отражённым лучами?

При изменении угла падения угол между падающим и отражённым лучами изменяется пропорционально. Угол между этими лучами равен удвоенному углу падения, поэтому если угол падения увеличить, угол между лучами также увеличится. Например, если угол падения 30°, то угол между лучами будет 60°, а при падении 45° он станет 90°. Таким образом, угол между лучами растёт вместе с увеличением угла падения.

Можно ли при отражении света получить угол между падающим и отражённым лучами меньше 90 градусов?

Нет, угол между падающим и отражённым лучами не может быть меньше 90 градусов. Поскольку угол между ними равен удвоенному углу падения, минимальное значение этого угла достигается при угле падения 0°, то есть при перпендикулярном падении луча на поверхность. В этом случае отражённый луч совпадает с падающим, и угол между ними равен нулю. При любом ненулевом угле падения угол между лучами будет больше или равен 90°, в зависимости от величины угла падения.

Как визуально понять, почему угол между падающим и отражённым лучами равен удвоенному углу падения?

Для понимания этого можно представить нормаль — воображаемую линию, перпендикулярную отражающей поверхности в точке падения луча. Падающий луч образует с нормалью угол падения, а отражённый луч — такой же угол, но с другой стороны нормали. Если мысленно сложить эти два угла вокруг нормали, получится угол между падающим и отражённым лучами, который равен сумме двух одинаковых углов, то есть удвоенному углу падения. Такой геометрический подход помогает наглядно увидеть, почему угол между лучами именно такой.

Как изменяется угол между падающим и отражённым лучами при изменении угла падения?

Угол между падающим и отражённым лучами всегда равен удвоенному углу падения относительно нормали к поверхности. Это связано с законом отражения, согласно которому угол падения равен углу отражения. Если угол падения увеличивается, то угол между двумя лучами также увеличивается, так как он равен удвоенному значению этого угла. Например, при угле падения 30° угол между лучами будет 60°, а при падении 45° – 90°. При этом угол не меняется произвольно, а строго подчиняется этим правилам, что можно проверить экспериментально с помощью зеркала и лазерного луча.

Почему угол между падающим и отражённым лучами не может быть меньше 0° или больше 180°?

Угол между падающим и отражённым лучами определяется как угол между двумя линиями, исходящими из одной точки на поверхности отражения. Поскольку падающий и отражённый лучи лежат по разные стороны от нормали, угол между ними не может быть меньше 0°, так как нулевой угол означал бы, что лучи совпадают по направлению, чего не бывает при отражении. С другой стороны, угол не может превышать 180°, потому что это максимальный угол, который может образовать две прямые на плоскости. В случае отражения угол строго ограничен законом, и его значение находится в диапазоне от 0 до 180°, при этом физически значимые углы лежат между этими пределами, так как отражённый луч не может уходить назад в сторону источника, а падающий луч всегда имеет направление к поверхности.