
Принцип Гюйгенса представляет собой фундаментальный метод анализа распространения световых волн, предложенный Кристианом Гюйгенсом в XVII веке. Он утверждает, что каждый точечный участок волнового фронта можно рассматривать как источник вторичных сферических волн. Последующая форма волнового фронта определяется огибающей этих вторичных волн. Эта концепция позволяет объяснить явления дифракции и интерференции с точностью, недоступной классической геометрической оптике.
Волновая оптика основывается на понимании природы света как волны, а принцип Гюйгенса служит важнейшим инструментом для моделирования поведения волн при прохождении через щели, вокруг препятствий и при отражении. Современные вычислительные методы используют принцип Гюйгенса для решения задач распространения электромагнитных волн в сложных средах, что критично для разработки оптических систем, лазеров и фотонных устройств.
Практическое применение принципа включает расчет распределения интенсивности света в зонах дифракции, прогнозирование фазовых сдвигов и построение моделей интерференционных картин. В частности, он лежит в основе теории Френеля и служит отправной точкой для более точных волнорных моделей, таких как теория Фраунгофера.
Понимание и корректное применение принципа Гюйгенса позволяет инженерам и исследователям оптимизировать оптические приборы и повышать качество изображений в микроскопии и телескопии. Кроме того, он обеспечивает теоретическую базу для развития технологий оптической связи и фотонных интегральных схем.
Механизм распространения волнового фронта по принципу Гюйгенса
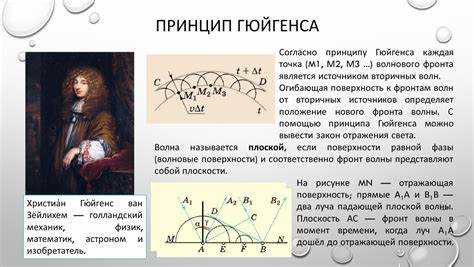
Принцип Гюйгенса описывает распространение волнового фронта как совокупность вторичных источников волн. Каждый точечный элемент фронта в момент времени t становится источником сферических волн малой амплитуды, которые распространяются с той же скоростью, что и исходная волна.
Новый волновой фронт в момент времени t + Δt образуется огибающей поверхностью этих вторичных сферических волн. Такая конструкция позволяет точно предсказать форму и направление распространения волны, включая явления отражения и преломления.
Важным аспектом механизма является учет фазового сдвига между вторичными волнами, что обеспечивает интерференционное сложение амплитуд. Это позволяет объяснить дифракцию света на препятствиях и краях, где классическая геометрическая оптика оказывается бессильной.
Рассчитывая положение нового фронта, следует учитывать, что амплитуды вторичных волн уменьшаются с расстоянием пропорционально 1/r, а фазовый сдвиг определяется длиной волны и временем распространения. Для практических расчетов применяются интегральные формулы Кирхгофа, основанные на принципе Гюйгенса.
Таким образом, принцип Гюйгенса не просто описывает движение фронта, а создает основу для количественного анализа сложных волновых процессов, делая его ключевым инструментом в волновой оптике и смежных областях.
Применение принципа Гюйгенса при объяснении интерференции света

Для анализа интерференционных полос применяют построение новых волновых фронтов с учетом фазовых сдвигов, возникающих на разных участках среды. Принцип Гюйгенса позволяет точно определить положения максимумов и минимумов интенсивности, основываясь на разности хода волн. В частности, для двух когерентных источников разность пути \(\Delta = m \lambda\) (где \(m\) – целое число, \(\lambda\) – длина волны) соответствует максимумам интерференции.
Использование принципа Гюйгенса облегчает расчет интенсивности света в сложных интерференционных системах, таких как многослойные покрытия и дифракционные решетки. На практике это помогает оптимизировать параметры оптических приборов и лазерных систем, улучшая качество изображения и минимизируя потери за счет управления фазой вторичных волн.
Роль принципа Гюйгенса в описании дифракционных явлений
Принцип Гюйгенса формирует базу для математического моделирования дифракции, позволяя рассматривать каждую точку волнового фронта как источник вторичных сферических волн. Это позволяет:
- Определять форму и интенсивность дифракционных картин, исходя из интерференции вторичных волн;
- Анализировать распространение волн в областях за препятствиями, где геометрическая оптика неприменима;
- Объяснять смещение и изменение яркости максимумов и минимумов дифракционной картины;
- Прогнозировать эффект огибания волной препятствий с размерами, сравнимыми с длиной волны.
Для практических расчетов дифракции принцип Гюйгенса дополняется методом Френеля, позволяющим интегрировать вклад всех вторичных источников с учетом фазовых сдвигов и амплитуд. Это позволяет получать точные распределения интенсивности в зоне дифракции, что критично для проектирования оптических систем и приборов.
Рекомендации для использования принципа в дифракционных расчетах:
- Выделять элементы волнового фронта с размерами порядка длины волны для корректного учета фазовых различий;
- Применять упрощения (плоские или сферические волны) в зависимости от геометрии задачи;
- Учитывать дополнительные граничные условия, возникающие при наличии сложных препятствий;
- Использовать численные методы интегрирования для сложных контуров и неоднородных сред.
Таким образом, принцип Гюйгенса не только обеспечивает качественное понимание дифракции, но и служит основой для точных количественных моделей, необходимых в современной оптике.
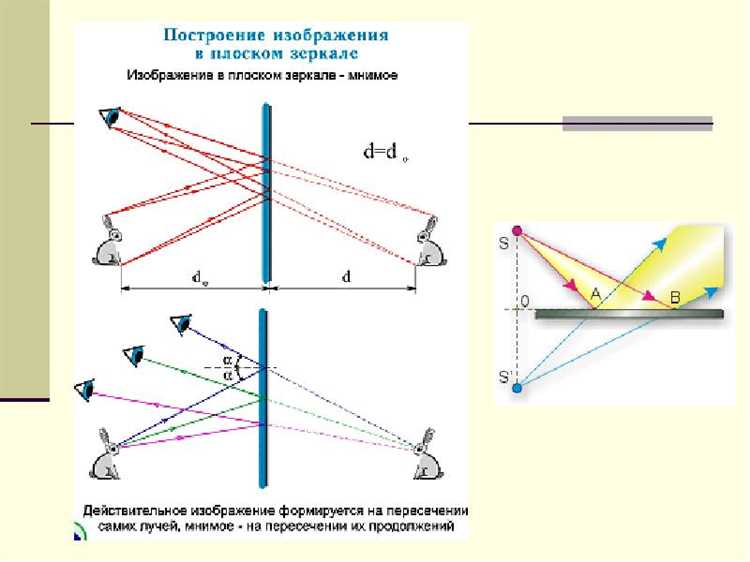
Как принцип Гюйгенса помогает моделировать отражение и преломление волн
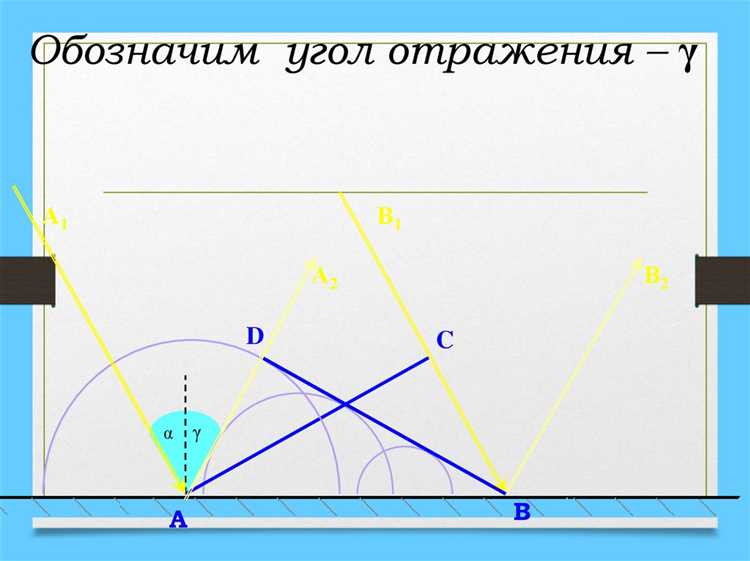
Принцип Гюйгенса рассматривает каждый точечный элемент волнового фронта как источник вторичных сферических волн. Для моделирования отражения волны анализ начинается с построения вторичных волн от поверхности раздела сред. Отражённый фронт формируется как огибающая этих волн, что позволяет точно определить направление и фазу отражённой волны без необходимости решать уравнения Максвелла полностью.
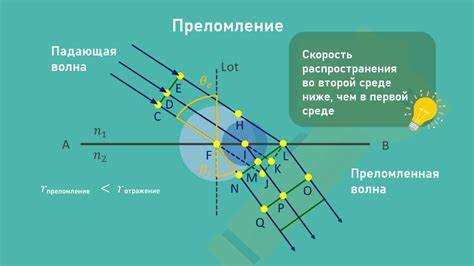
При преломлении принцип Гюйгенса применяется к переходу волны через границу двух сред с разной скоростью распространения. Вторичные волны в новой среде распространяются с изменённой скоростью, что приводит к изменению направления волнового фронта согласно закону Снелла. Такой подход позволяет наглядно визуализировать и вычислить угол преломления, основываясь на соотношении скоростей и длинах волн в обеих средах.
Для практического моделирования отражения и преломления следует:
- Разбить исходный волновой фронт на множество точечных источников, распределённых с шагом, меньше длины волны.
- Рассчитать вторичные волны для каждого источника с учётом скорости и направления распространения в соответствующей среде.
- Определить огибающую вторичных волн, которая и задаст форму нового волнового фронта.
- Для интерфейса сред учитывать разницу фаз и амплитуд, вызванных отражением и преломлением, применяя граничные условия.
Использование принципа Гюйгенса обеспечивает точное моделирование сложных оптических явлений без необходимости решения сложных дифференциальных уравнений, что существенно упрощает анализ оптических систем и способствует разработке новых материалов с заданными свойствами отражения и преломления.
Использование принципа Гюйгенса для расчёта фазовых изменений волн

Принцип Гюйгенса рассматривает каждую точку волнового фронта как источник вторичных сферических волн. Для вычисления фазовых изменений волны в заданной точке пространства необходимо суммировать амплитуды и фазы всех вторичных источников, расположенных на предыдущем волновом фронте.
Фазовый сдвиг волны в точке наблюдения определяется разницей оптических путей от каждого вторичного источника до этой точки. Если обозначить фазу на волновом фронте как φ₀, расстояние от источника i до точки наблюдения как rᵢ, а длину волны как λ, то вклад i-го источника в фазу можно выразить как:
φᵢ = φ₀ + (2π/λ)·rᵢ
Интегрирование амплитуд с учётом фазовых сдвигов проводится по всей поверхности волнового фронта, что позволяет определить результирующую амплитуду и фазу в точке наблюдения. Для упрощения вычислений часто применяют приближение Френеля, ограничивающее интеграл областью с учётом значимого вклада вторичных волн.
Рекомендуется применять численные методы, такие как дискретизация поверхности волнового фронта с шагом, не превышающим половины длины волны, для точного расчёта фазовых изменений. Это позволяет учитывать интерференционные эффекты и фазовые модуляции, возникающие при прохождении волн через неоднородные среды и препятствия.
Ограничения принципа Гюйгенса в современных оптических системах
Принцип Гюйгенса эффективно описывает распространение волн в классической волновой оптике, однако при проектировании высокоточных и нанометровых оптических систем его применение становится ограниченным. Во-первых, принцип не учитывает явления интерференции и когерентности света напрямую, что критично при анализе сложных интерферометрических схем и лазерных резонаторов. Во-вторых, приближение Гюйгенса не учитывает фазовые сдвиги, возникающие на границах сред с резкими показателями преломления, что ведет к ошибкам в моделировании дифракционных эффектов на микро- и наноструктурах.
Кроме того, принцип Гюйгенса не применим для описания волн с сильно выраженной поляризацией, так как он не учитывает векторную природу электромагнитного поля. В современных системах с использованием плазмонных наноструктур и метаматериалов требуется более полная теория, основанная на уравнениях Максвелла, которая способна корректно описывать нелокальные эффекты и анизотропию среды.
При проектировании оптических систем с малыми апертурами и высокими числовыми апертурами эффект так называемой «краевой дифракции» не может быть адекватно смоделирован с помощью принципа Гюйгенса. В таких случаях рекомендуется использовать методы, основанные на дифракции Фраунгофера или Френеля с численным решением уравнений волнового фронта.
Для повышения точности моделирования распространения света в системах с микроструктурированной поверхностью необходимо комбинировать принцип Гюйгенса с численными методами, такими как метод конечных элементов или метод конечных разностей по времени. Это позволяет учитывать сложное взаимодействие волн с наноразмерными объектами и минимизировать погрешности.
Таким образом, несмотря на фундаментальную роль принципа Гюйгенса, в современных оптических технологиях его используют преимущественно как начальный приближённый инструмент, дополняя более точными вычислительными методами и полным электромагнитным анализом.
Связь принципа Гюйгенса с волновой природой света и современными теориями
Принцип Гюйгенса формулирует световое распространение как совокупность вторичных волн, возникающих из каждой точки фронта волны. Это фундаментальное представление стало основой для волновой оптики и позволило объяснить дифракцию и интерференцию, которые невозможно адекватно описать в рамках корпускулярной модели.
Современная физика рассматривает свет как электромагнитную волну, что подтверждает Максвелловы уравнения, связывающие электрические и магнитные поля с распространением волн в пространстве. Принцип Гюйгенса совместим с этой моделью, так как вторичные волны интерпретируются как локальные возмущения электромагнитного поля, расширяющиеся со скоростью света.
В квантовой теории света принцип Гюйгенса сохраняет свое значение в представлении волновой функции фотонов, где волновая природа описывает вероятность обнаружения квантов в конкретных точках пространства. При этом принцип позволяет моделировать интерференционные эффекты, возникающие в экспериментах с отдельными фотонами.
Для точного вычисления распространения световых волн сегодня широко применяются численные методы, основанные на принципе Гюйгенса-Френеля и интегральных уравнениях, что существенно улучшает прогнозы в системах с комплексной геометрией и неоднородными средами.
Рекомендации для практического применения включают использование принципа Гюйгенса при проектировании оптических устройств с малыми масштабами, где волновые эффекты критичны. Это актуально для фотоники, микрооптики и лазерных технологий, где корректное моделирование света позволяет повысить эффективность и качество работы систем.
Вопрос-ответ:
Что такое принцип Гюйгенса и как он объясняет распространение света?
Принцип Гюйгенса основывается на идее, что каждая точка на волновом фронте может рассматриваться как источник новых вторичных волн. Эти вторичные волны распространяются во всех направлениях с одинаковой скоростью. Новый волновой фронт в следующий момент времени формируется как огибающая всех этих волн. Этот подход помогает понять, каким образом свет распространяется, изменяет направление и взаимодействует с препятствиями.
Как применение принципа Гюйгенса помогает объяснить явления интерференции и дифракции?
Используя принцип Гюйгенса, можно представить, что при прохождении света через узкие щели или при наложении двух световых волн, каждая точка волнового фронта порождает вторичные волны. Их взаимодействие приводит к возникновению характерных узоров, которые мы называем интерференцией и дифракцией. Так, интерференция возникает из-за сложения волн с разной фазой, а дифракция — из-за отклонения волн при прохождении через препятствия или щели. Благодаря этому принципу можно математически и визуально моделировать эти эффекты.
В чём отличие подхода Гюйгенса от представления света как потока частиц?
Подход Гюйгенса рассматривает свет как волну, распространяющуюся через пространство с помощью вторичных источников, что позволяет объяснять такие явления, как интерференция и дифракция, которые не поддаются описанию в рамках чисто корпускулярной теории. Корпускулярная теория, где свет представлен частицами, успешно объясняет отражение и преломление, но не может полностью описать волновые свойства света. Принцип Гюйгенса ввёл волновую модель, дающую более глубокое понимание природы света.
Почему принцип Гюйгенса важен для развития оптики и науки в целом?
Принцип Гюйгенса стал одним из фундаментальных законов в волновой оптике, обеспечив основу для последующих исследований и теорий, включая теорию Максвелла и квантовую механику. Он помог систематизировать понимание распространения световых волн и объяснить ряд явлений, которые не удавалось понять ранее. Благодаря ему стали возможны точные расчёты и прогнозы поведения света в различных условиях, что нашло применение в оптических приборах, технологиях связи и научных экспериментах.
Какие ограничения существуют у принципа Гюйгенса и как они были преодолены?
Хотя принцип Гюйгенса эффективно описывает распространение волн, он не учитывает явления дифракционного интерференционного характера в деталях, например, интенсивность и амплитуду вторичных волн. Эти ограничения были устранены позже благодаря развитию волновой теории Максвелла, где свет представлен как электромагнитная волна. Также теория Френеля дополнила принцип, учитывая интерференцию вторичных волн с фазовыми сдвигами. Современная физика использует эти расширенные модели для более точного описания поведения света.
Как принцип Гюйгенса помогает понять распространение световых волн?
Принцип Гюйгенса рассматривает каждую точку волнового фронта как источник новых, маленьких волн — так называемых вторичных волн. Распространение света можно представить как наложение этих вторичных волн, что позволяет объяснить, как волна движется дальше, изменяет направление и формирует новые фронты. Это особенно полезно для описания явлений, таких как дифракция и интерференция, которые невозможно объяснить с помощью простого представления света как прямолинейных лучей.






