Как найти к в электростатике

В задачах электростатики коэффициент k (или ε₀, диэлектрическая проницаемость вакуума) имеет ключевое значение для расчета электрических полей и взаимодействий между зарядами. Он появляется в уравнении Кулона и влияет на силы, действующие между зарядами. Понимание его роли позволяет точнее моделировать физические процессы в различных материалах и средах.

Коэффициент k связан с характеристиками вакуума и является фундаментальной физической константой. Его значение равно 8.854 × 10⁻¹² Ф/м. В реальных задачах электростатики его роль часто становится более заметной в зависимости от среды, в которой происходят взаимодействия, поскольку диэлектрическая проницаемость среды (ε) определяет влияние на электрическое поле и заряд.

Чтобы найти коэффициент k в контексте конкретной задачи, необходимо учесть не только физическое значение вакуума, но и воздействие на него внешних факторов, таких как плотность зарядов или геометрия системы. Влияние диэлектрических материалов может изменять поле и силу взаимодействия, что также следует учитывать при вычислениях.

Определение коэффициента k в контексте закона Кулона

В электростатике коэффициент k (или постоянная Кулона) используется для количественного выражения силы взаимодействия между двумя точечными зарядами. Закон Кулона описывает силу, действующую между двумя зарядами, как пропорциональную произведению величин зарядов и обратно пропорциональную квадрату расстояния между ними. Он имеет вид:

F = k * (q1 * q2) / r²,

где F – сила взаимодействия между зарядами, q1 и q2 – величины зарядов, r – расстояние между ними. Коэффициент k учитывает характеристики среды, в которой находятся заряды, и определяется как:

k = 1 / (4π * ε0),

где ε0 – электрическая постоянная (пермиттивность вакуума), её значение составляет 8.854 × 10⁻¹² Ф/м.

Таким образом, постоянная Кулона для вакуума равна:

k ≈ 8.988 × 10⁹ Н·м²/Кл².

При изменении среды коэффициент k может изменяться, что связано с диэлектрической проницаемостью материала, в котором находятся заряды. Для материала с диэлектрической проницаемостью ε коэффициент будет равен:

k = 1 / (4π * ε),

где ε = ε0 * εr, а εr – относительная диэлектрическая проницаемость материала.

Понимание и точное использование коэффициента Кулона критично для корректного расчёта сил взаимодействия в системах с электрическими полями, особенно при работе с различными материалами и при расчётах в нестандартных условиях.

Как использовать коэффициент k при расчете сил между зарядами

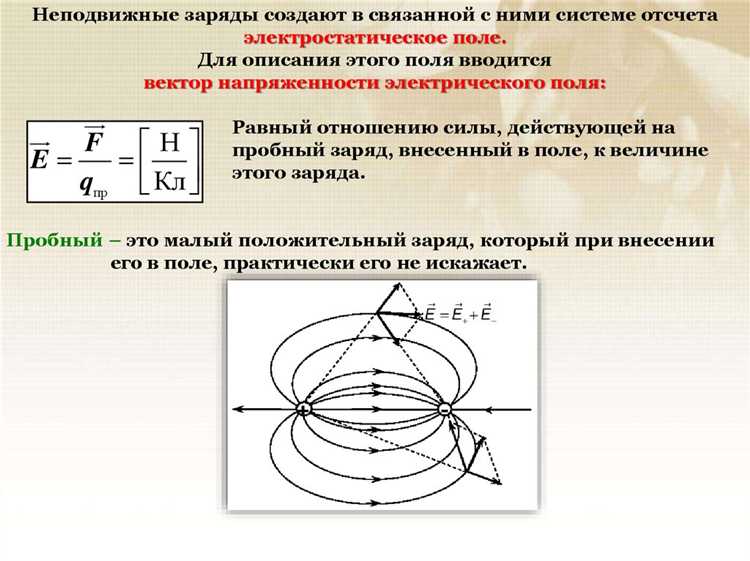
Коэффициент k, или постоянная электростатического взаимодействия, используется для расчета силы между двумя точечными зарядами. Его значение равно 8,99 × 10⁹ Н·м²/Кл² и остается постоянным в системе СИ. Этот коэффициент используется в законе Кулона, который описывает силу F между двумя зарядами:

F = k * (|q₁ * q₂|) / r²

Здесь:

• F – сила взаимодействия между зарядами,
• k – коэффициент электростатического взаимодействия (8,99 × 10⁹ Н·м²/Кл²),
• q₁ и q₂ – величины зарядов,
• r – расстояние между зарядами.

Для корректного применения коэффициента k важно учитывать следующее:

1. Единицы измерений: Заряды должны быть в кулонах (Кл), а расстояние – в метрах (м). Сила будет измеряться в ньютонах (Н).
2. Знаки зарядов: Если оба заряда одинаковы по знаку (оба положительные или оба отрицательные), сила будет отталкивающей. Если заряды противоположные, сила будет притягивающей.
3. Использование правильных значений: При использовании коэффициента k в расчетах важно не путать систему единиц. Для других единиц измерения могут потребоваться другие значения коэффициента.

Пример расчета:

• Даны два заряда: q₁ = 2 × 10⁻⁶ Кл и q₂ = 3 × 10⁻⁶ Кл, расстояние между ними r = 0,5 м.
• Применяем формулу:

F = (8,99 × 10⁹) * (|2 × 10⁻⁶ * 3 × 10⁻⁶|) / (0,5)²
F = (8,99 × 10⁹) * (6 × 10⁻¹²) / 0,25
F = 2,16 Н

Таким образом, сила взаимодействия между зарядами составляет 2,16 Н.

При решении задач важно также учитывать, что коэффициент k применим только в вакууме. В средах с другими диэлектрическими свойствами, например, в воздухе, коэффициент может изменяться в зависимости от диэлектрической проницаемости среды, что также влияет на расчет силы.

Коэффициент k в задаче с диэлектриками: влияние материала на электростатику

Коэффициент k, или диэлектрическая проницаемость материала, играет ключевую роль в решении задач электростатики, где присутствуют диэлектрики. Влияние материала на электростатическое поле выражается через изменение величины электрического поля и силы взаимодействия зарядов.

Для вакуума коэффициент k равен единице, но для диэлектрических материалов k значительно больше. Это значение зависит от структуры и свойств вещества. Например, в стекле или парафине коэффициент может быть порядка 2-4, в то время как в воде – около 80 при комнатной температуре.

Когда диэлектрик размещается в электрическом поле, его атомы или молекулы поляризуются, что приводит к ослаблению общего электрического поля внутри материала. Это ослабление определяется коэффициентом k. Чем выше значение k, тем сильнее уменьшается электрическое поле в материале. Это явление важно для таких процессов, как зарядка конденсаторов и распределение поля в изоляторе.

Для точных расчетов необходимо учитывать, что значение k изменяется с температурой и частотой поля. При высоких частотах диэлектрические свойства могут изменяться из-за диссипации энергии и внутренних сопротивлений материала.

Кроме того, в задачах с несколькими диэлектриками влияние каждого материала на систему будет зависеть от его положения в поле. Например, в многослойных структурах или при наличии границ между различными материалами важно учитывать как изменяется коэффициент k на стыке материалов. Это нужно для корректного расчета потенциала и поля в таких системах.

Влияние расстояния на величину коэффициента k при взаимодействии зарядов

В электростатике коэффициент k, или константа электрического взаимодействия, зависит от расстояния между зарядами. Этот коэффициент определяется формулой: k = 1 / (4πε), где ε – диэлектрическая проницаемость среды. В вакууме значение ε0 равно 8.854 × 10⁻¹² Ф/м.

При взаимодействии двух точечных зарядов сила их взаимного притяжения или отталкивания пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними. Это выражается в законе Кулона: F = k * (q₁ * q₂) / r². В данной формуле r – это расстояние между зарядами, а k – это коэффициент, который зависит от типа среды, в которой находятся заряды.

Изменение расстояния между зарядами прямо влияет на силу взаимодействия. Увеличение r в два раза снижает силу взаимодействия в четыре раза. Коэффициент k в этом контексте действует как зависимая величина, и его величина зависит от среды. Для вакуума k сохраняет фиксированное значение, а при изменении среды, например, при переходе в диэлектрический материал, значение ε увеличивается, что снижает k.

Таким образом, расстояние оказывает косвенное влияние на величину коэффициента k, изменяя силу электростатического взаимодействия через параметр ε среды. Практически это означает, что в случае увеличения расстояния между зарядами сила их взаимодействия уменьшается, что имеет важное значение при моделировании процессов в электрических цепях и устройствах, чувствительных к изменениям расстояний между зарядами.

Коэффициент k в вычислениях электростатической энергии системы

Коэффициент k, также известный как электростатическая постоянная или константа, играет ключевую роль в расчетах электростатической энергии системы зарядов. Это физическая величина, которая определяет силу взаимодействия между электрическими зарядами в вакууме. Его значение составляет примерно 8.85 × 10⁻¹² Кл²/Н·м² в системе СИ, но в разных единицах измерения может варьироваться. Коэффициент k включается в формулы для вычисления потенциала и энергии взаимодействия зарядов.

Электростатическая энергия системы, состоящей из нескольких зарядов, может быть найдена через формулу:

E = (1 / (4πε₀)) Σ Σ (qᵢ qⱼ / rᵢⱼ),

где E – электростатическая энергия, qᵢ и qⱼ – величины зарядов, rᵢⱼ – расстояние между ними, ε₀ – электрическая постоянная, а k = 1 / (4πε₀) – коэффициент взаимодействия.

При расчете энергии взаимодействия важно учитывать, что значение k в расчетах используется для корректировки силы между зарядами в вакууме. Это значение позволяет правильно учесть эффекты дальнодействия, то есть уменьшение силы взаимодействия с увеличением расстояния между объектами.

При решении задач электростатики с несколькими зарядами на практике коэффициент k используется для вычислений как в контексте взаимодействия точечных зарядов, так и для сложных систем с распределенными зарядами. Понимание точной роли этого коэффициента в расчетах позволяет повысить точность моделей и избегать ошибок в аналитических решениях.

Коэффициент k также имеет важное значение в расчетах для других типов электростатических систем, например, при моделировании поля вокруг проводников, что требует особого подхода в вычислениях. Здесь значение k будет влиять на расчет плотности поля и распределения потенциала, что имеет прямое отношение к задачам для систем с неоднородными зарядами или при наличии проводящих материалов.

Практические методы измерения коэффициента k в лабораторных условиях

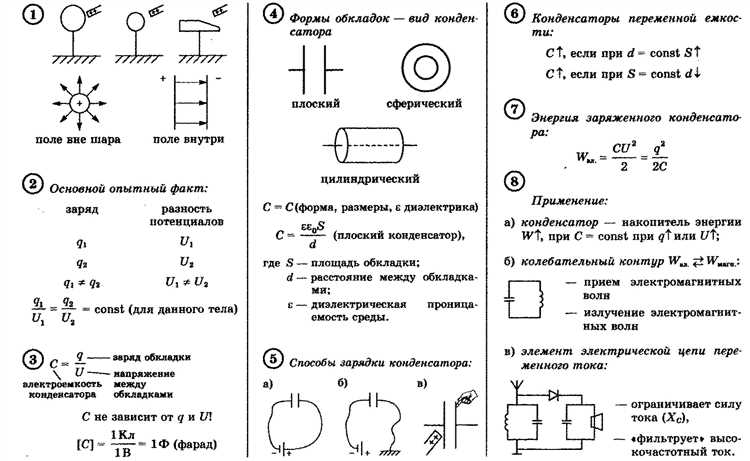
Измерение коэффициента k в задачах электростатики требует точных методов, основанных на использовании стандартных физических приборов. Один из распространённых способов – метод измерения электрической ёмкости конденсатора. Этот метод предполагает использование конденсатора с известными геометрическими размерами, где коэффициент k можно вычислить, основываясь на изменении ёмкости при изменении диэлектрической среды между пластинами.

Для выполнения эксперимента с конденсатором необходимо подключить его к измерительному устройству, например, к ёмкостному вольтметру или мосту Уитстона. Важно, чтобы условия измерений оставались постоянными, включая температуру, которая может существенно повлиять на результаты. При изменении диэлектрической среды между пластинами, ёмкость конденсатора будет изменяться пропорционально коэффициенту k.

Другим методом является использование электрического поля между проводниками. В данном случае можно измерить напряжение и ток в замкнутом контуре, что позволит через закон Кулона вычислить коэффициент k, принимая во внимание геометрию системы. Метод хорош тем, что позволяет получать значения коэффициента при различных конфигурациях зарядов и материалов, а также проводить эксперимент при различной геометрии проводников.

При измерении коэффициента k важно соблюдать точность в установке оборудования и использовать приборы с минимальной погрешностью. К примеру, использование мостовых измерений с высокой точностью позволяет исключить влияние погрешностей измерений, таких как дрейф показаний приборов.

Для повышения точности результатов можно использовать методику, основанную на сравнении измерений с теоретическими значениями. В этом случае необходимо создать систему с известными параметрами и точно измерить соответствующие физические величины, такие как электрическая ёмкость, напряжение или поле. Разница между теоретическими и экспериментальными данными даст значение коэффициента k.

Ключевыми аспектами при проведении лабораторных измерений являются минимизация внешних помех, точность калибровки измерительных приборов и учёт всех факторов, влияющих на электрические характеристики системы. Это позволяет существенно повысить достоверность получаемых данных при определении коэффициента k в задачах электростатики.

Типичные ошибки при применении коэффициента k в расчетах электростатики

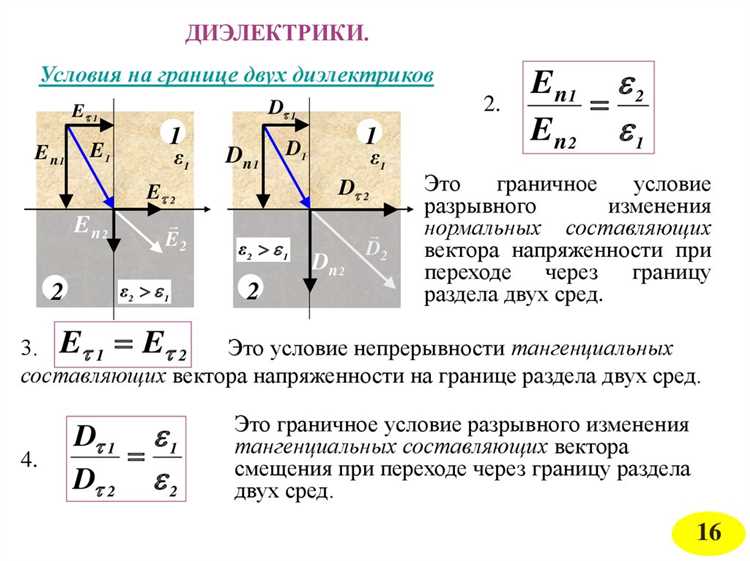
При решении задач электростатики с использованием коэффициента k (величина, определяющая электрическую проницаемость среды) важно точно понимать его значение и особенности применения. Ошибки, связанные с этим коэффициентом, могут существенно повлиять на точность расчетов.

• Неверное использование значения коэффициента k. Важно помнить, что коэффициент k зависит от типа среды. Для вакуума его значение равно 1, а для других материалов оно может сильно варьироваться. При расчете взаимодействия зарядов в разных средах часто ошибаются, принимая для всех веществ одно и то же значение k, что ведет к неправильным результатам.
• Игнорирование влияния температуры на k. Электрическая проницаемость может изменяться в зависимости от температуры, особенно в случае веществ с высокой чувствительностью. Игнорирование этого фактора может привести к погрешностям, особенно в задачах, требующих точных измерений.
• Неправильное применение формул для различных сред. В расчетах для различных типов сред (диэлектрики, проводники, вакуум) важно использовать правильные уравнения. Например, при расчете силы взаимодействия между двумя зарядами в диэлектрике коэффициент k отличается от значения, используемого для вакуума. Ошибки в выборе соответствующей формулы – частая причина неверных результатов.
• Неучет неоднородности среды. В реальных задачах часто приходится работать с неоднородными средами, где коэффициент k варьируется по пространству. Использование среднего значения k вместо переменного приводит к значительным погрешностям, особенно если материал имеет четкую границу или сильные колебания в свойствах.
• Ошибки в единицах измерения. Коэффициент k может выражаться в разных единицах, что также является частой причиной ошибок. Важно помнить, что в международной системе единиц (СИ) электрическая проницаемость среды указывается безразмерно, а в других системах (например, в единицах СГС) она может иметь другие значения. Преобразование между системами требует внимательности.

Для минимизации ошибок следует тщательно проверять данные о материале, уточнять условия задачи и, при необходимости, проводить экспериментальные измерения. Правильное использование коэффициента k требует внимательности и точности, так как даже небольшие погрешности могут значительно изменить результаты расчетов.

Вопрос-ответ:

Как можно найти коэффициент \(k\) в задаче электростатики?

Коэффициент \(k\) обычно обозначает электрическую постоянную, которая зависит от выбранной системы единиц. В международной системе единиц (СИ) это значение равно \(k = 8.99 \times 10^9 \, \text{Н} \cdot \text{м}^2 / \text{Кл}^2\). Это значение используется при вычислении силы взаимодействия между двумя зарядами в законе Кулона.

Что означает диэлектрическая проницаемость в контексте нахождения коэффициента \(k\)?

Диэлектрическая проницаемость (\(\epsilon\)) — это величина, которая характеризует способность вещества поляризоваться под действием электрического поля. Для вакуума \(\epsilon_0 = 8.85 \times 10^{-12} \, \text{Ф/м}\). Если электростатическое взаимодействие происходит в материале, то коэффициент \(k\) будет зависеть от \(\epsilon\) этого материала, что изменяет силу взаимодействия зарядов по сравнению с вакуумом.

Почему коэффициент \( k \) в задачах электростатики имеет разные значения в разных системах единиц, и как это влияет на решение задач?

Коэффициент \( k \), который используется в законе Кулона для описания взаимодействия зарядов, зависит от системы единиц. В Международной системе единиц (СИ) этот коэффициент равен \( 8.99 \times 10^9 \, \text{Н} \cdot \text{м}^2/\text{Кл}^2 \), но в других системах, например, в системе СГС (сантиметр-грамм-секунда), значение коэффициента будет другим. В системе СГС его значение составляет \( 1 \). Это связано с различиями в единицах измерений и величинах, которые используются для расчётов. При решении задач важно быть внимательным к системе единиц, чтобы корректно применять значение коэффициента и не допустить ошибок в расчётах. Если система единиц меняется, нужно пересчитать все величины с учётом новых коэффициентов для обеспечения правильности решений.