Как найти угол отражения если известен угол падения

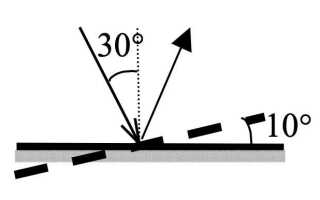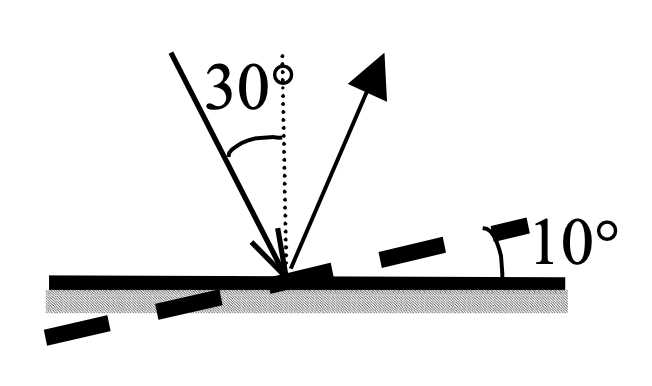
При анализе взаимодействия световых или радиоволновых лучей с поверхностями важно понимать, как определить угол отражения. Это необходимо в геодезии, оптике, радиолокации, а также в архитектурном моделировании освещения. Формула отражения проста, но требует точного понимания условий, при которых она применима.

Угол падения измеряется между падающим лучом и перпендикуляром к отражающей поверхности в точке контакта. Этот же принцип применяется к углу отражения – он также отсчитывается от нормали, а не от поверхности. Согласно закону отражения, угол отражения всегда равен углу падения: θ_{отражения} = θ_{падения}.

Чтобы вычислить угол отражения, достаточно измерить угол между направлением падающего луча и нормалью к поверхности. Например, если падающий луч образует угол 35° с нормалью, то отражённый луч также отойдёт под углом 35° с противоположной стороны этой нормали. Важно: при наклонной или искривлённой поверхности нормаль должна быть определена в конкретной точке контакта, иначе расчёт будет неточным.

При проведении практических измерений используют лазерные уровни, оптические прицелы или угломерные инструменты. Для вычислений в программных средах применяют векторы: отражённый вектор определяется с использованием формулы R = I − 2(N · I)N, где I – падающий вектор, N – нормаль. Такой подход особенно важен в 3D-графике и симуляциях физики.

Что такое угол падения и как его правильно измерить

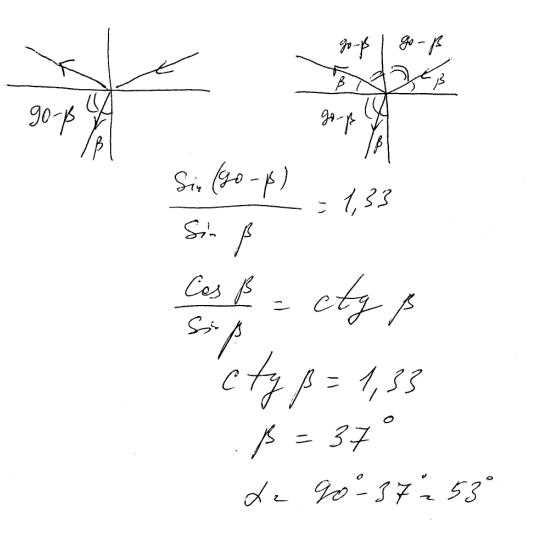
Для точного измерения угла падения необходимо использовать оптический транспортир или гониометр. Прибор устанавливают так, чтобы его центр совпадал с точкой падения луча. Нормаль выстраивают с помощью отвеса или лазерного уровня. Угол фиксируют между направлением падающего луча и этой нормалью.

В лабораторных условиях используют лазерный источник и экран. Луч направляют на исследуемую поверхность, а затем фиксируют положение отражённого и падающего лучей. При известном расстоянии до экрана и смещении пятна света угол падения можно вычислить через арктангенс отношения смещения к расстоянию. Такая методика позволяет определить угол с точностью до десятых долей градуса.

Формула расчета угла отражения: пошаговое объяснение

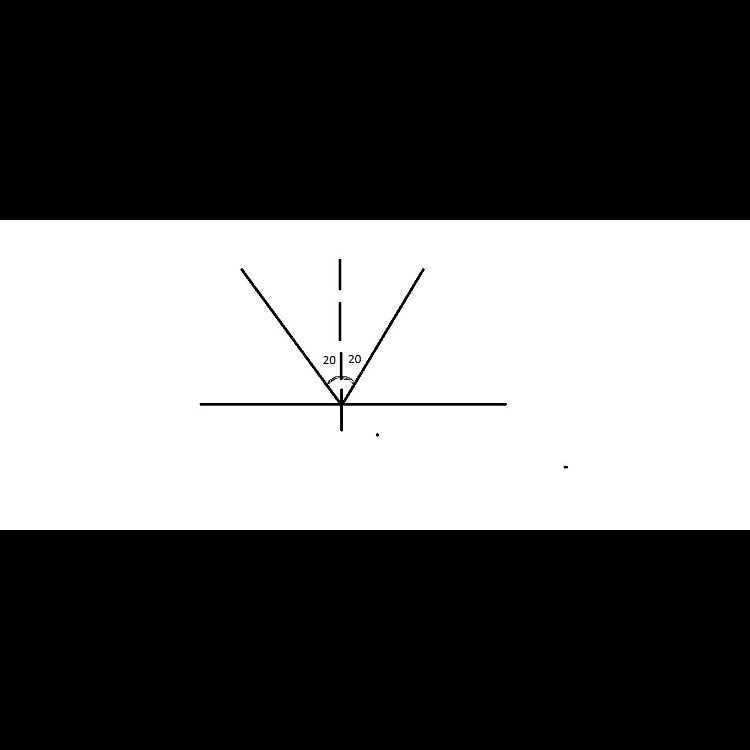
Отражение света, звука или радиоволн подчиняется одному и тому же геометрическому принципу: угол отражения равен углу падения. Это утверждение базируется на законе отражения, который формулируется следующим образом:

Угол отражения (θ_отр) = Угол падения (θ_пад)

Оба угла измеряются относительно нормали – перпендикуляра к отражающей поверхности в точке падения луча. Чтобы точно рассчитать угол отражения, выполните следующие действия:

1. Определите точку соприкосновения падающего луча с поверхностью.
2. Проведите нормаль – прямую, перпендикулярную к поверхности в этой точке.
3. Измерьте угол между падающим лучом и нормалью. Это и есть угол падения (θ_пад).
4. Примите, что угол отражения (θ_отр) будет точно таким же, но в противоположном направлении от нормали.

Если угол падения известен в числовом виде, например, 42°, то угол отражения также будет равен 42°. При этом важно: углы измеряются не относительно поверхности, а именно относительно нормали. Ошибки в построении нормали приводят к неправильному расчету.

Формально:

Если работа ведется с наклонными или изогнутыми поверхностями, необходимо сначала построить касательную в точке контакта, затем – нормаль, и только после этого определять угол. В практической оптике и акустике часто применяются гониометры или лазерные указки для точного измерения углов.

Как определить нормаль к поверхности для построения углов

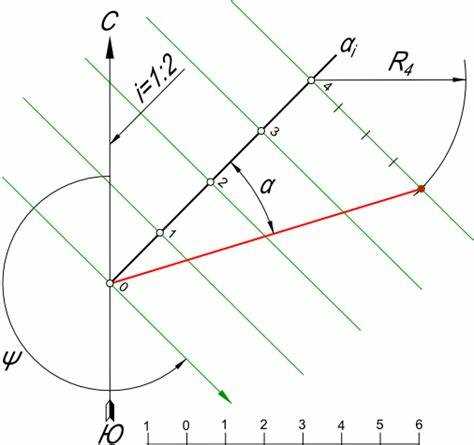
Для плоских поверхностей нормаль определяется по ориентации самой плоскости. Например, для горизонтальной поверхности нормаль направлена вертикально вверх. Если поверхность наклонена, нормаль можно построить как вектор, перпендикулярный плоскости в заданной точке. Это делается с использованием координатных направляющих или по известным углам наклона относительно горизонтали.

Для вычисления нормали в 3D-пространстве при задании поверхности тремя точками A, B и C, используйте векторное произведение векторов AB и AC:

N = AB × AC. После получения вектора нормали важно его нормализовать, то есть привести к единичной длине, чтобы обеспечить корректные расчёты углов:
N_normalized = N / |N|.

В случае криволинейных поверхностей, нормаль вычисляется как градиент функции поверхности в данной точке. Например, если поверхность описывается уравнением z = f(x, y), то нормаль определяется как вектор:

N = (-∂f/∂x, -∂f/∂y, 1),

затем нормализуется аналогично.

Для точек на моделируемых поверхностях в графических или инженерных системах нормали обычно рассчитываются автоматически. В ручных расчётах необходимо строго придерживаться описанных методов, особенно при анализе сложных отражений на изогнутых формах.

Примеры расчета угла отражения на гладкой и шероховатой поверхностях

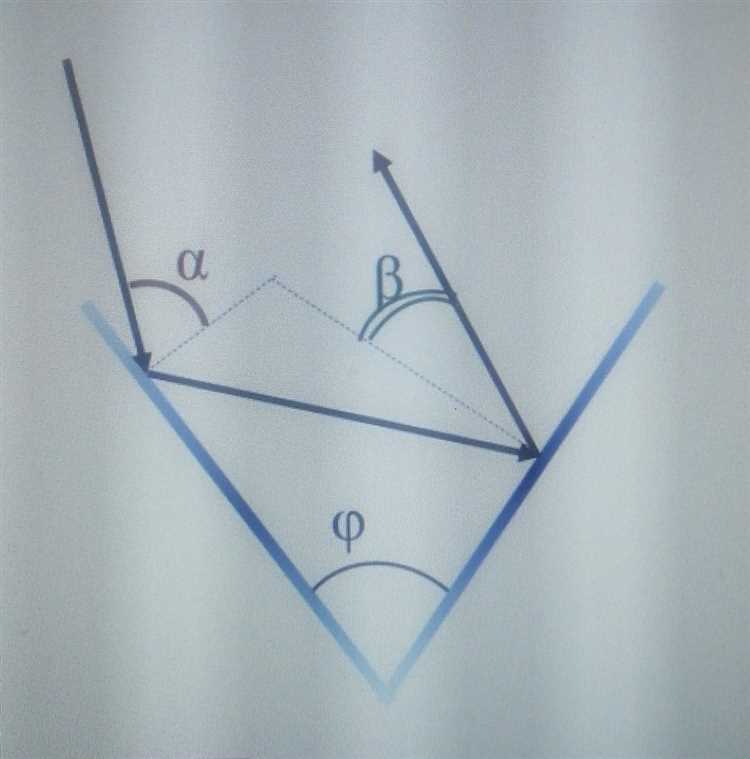
При падении светового луча на идеально гладкую поверхность угол отражения равен углу падения. Например, если луч падает под углом 45° к нормали, отражение произойдет также под углом 45° в противоположную сторону относительно нормали. Это правило справедливо для зеркал, стеклянных плит и полированных металлических поверхностей.

Для расчета на шероховатой поверхности применяют понятие диффузного отражения. Здесь отражение происходит под множеством углов из-за микронеровностей. Если направить луч под углом 30° к нормали на бетонную стену, часть энергии отразится примерно в диапазоне от 10° до 50° с постепенным ослаблением интенсивности. Точный расчет проводят с учетом статистического распределения микроскопических наклонов. Применяют модели, такие как модель Ламберта, при которой интенсивность отражения пропорциональна косинусу угла между направлением отражения и нормалью к поверхности.

Если поверхность условно шероховатая, например матовая краска, и известен средний угол наклона микронеровностей – скажем, 15°, тогда при падении луча под 60° большая часть отражения произойдет в пределах ±15° от 60°, то есть в диапазоне от 45° до 75°. Это полезно при расчетах рассеяния в оптических системах или при проектировании освещения.

Распространенные ошибки при измерении углов и как их избежать

Нарушения в точности измерения углов падения и отражения нередко приводят к искажённым результатам. Ниже приведены конкретные ошибки и способы их предотвращения.

• Неправильное определение нормали. Угол падения измеряется относительно перпендикуляра к поверхности, а не к самой поверхности. Ошибка в определении нормали даже на 2–3° приводит к зеркальной ошибке в угле отражения. Используйте лазерный уровень или транспортер с отвесом для точной фиксации нормали.
• Наклон прибора измерения. Если прибор (транспортир, гониометр) установлен не строго горизонтально, возникает систематическая погрешность. Проверяйте горизонтальность поверхности с помощью строительного уровня перед началом измерений.
• Чтение углов с параллаксом. При взгляде на шкалу под углом показания искажаются. Убедитесь, что глаз находится строго напротив метки. Лучше использовать приборы с цифровыми датчиками или зеркальными шкалами, устраняющими параллакс.
• Смещение источника или точки наблюдения. Даже небольшое отклонение от предполагаемой геометрии приводит к нарушению закона отражения. Устанавливайте источник и приемник излучения на направляющих с фиксированным положением.
• Неточная калибровка угломерного оборудования. Приборы требуют периодической поверки. Используйте эталонные углы (например, прецизионные угловые блоки) для проверки точности перед началом эксперимента.
• Игнорирование толщины поверхности. При работе с прозрачными или многослойными материалами, отражение может происходить не с верхнего слоя. Учитывайте оптические свойства материала и при необходимости применяйте корректировку на преломление.

Точная настройка оборудования, соблюдение геометрии измерений и регулярный контроль исправности приборов – ключ к минимизации погрешностей при определении углов отражения.

Применение закона отражения в школьных и лабораторных задачах

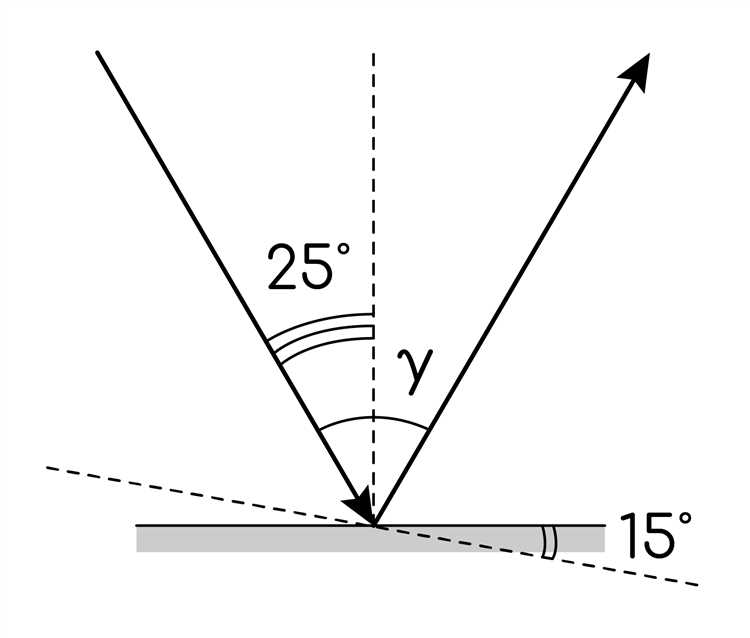
Закон отражения гласит: угол отражения равен углу падения, что позволяет точно рассчитывать траектории лучей при взаимодействии с поверхностями. В школьных экспериментах эта закономерность применяется для построения моделей отражения света, звука и других волн, а также для проверки гипотез по геометрии отражения.

Практическое задание: измерение угла падения и угла отражения с помощью транспортиров и зеркала. Рекомендуется использовать световой луч, направленный под известным углом к плоской отражающей поверхности, и фиксировать углы по граням транспортиров. Полученные значения следует сравнить с теоретическим равенством углов для проверки точности эксперимента.

В лабораторных условиях закон отражения применяется при настройке оптических приборов, например, лазерных систем и интерферометров. При проектировании отражающих элементов важно учитывать идеальность поверхности для минимизации рассеяния и сохранения угла отражения.

Для решения задач с несколькими отражениями в школьных упражнениях используется последовательное применение закона отражения. Практические примеры включают моделирование траекторий световых лучей в призмах и зеркальных лабиринтах, что помогает развивать пространственное мышление и умение работать с углами.

Рекомендуется включать измерения с минимальной погрешностью, учитывать толщину линии луча и точность установки оборудования. Это повышает качество полученных результатов и способствует глубокому пониманию физической сути отражения.

Вопрос-ответ:

Как соотносится угол отражения с углом падения света на поверхность?

Угол отражения равен углу падения — это один из основных законов отражения света. Это значит, что луч, падающий на поверхность под определённым углом к перпендикуляру, отразится под тем же углом, но с противоположной стороны нормали.

Можно ли вычислить угол отражения, если поверхность не гладкая, а шероховатая?

Для шероховатых поверхностей отражение становится рассеянным, и понятие точного угла отражения теряет смысл. В таких случаях отражённый свет распределяется по разным направлениям, и простой расчёт по углу падения не подходит.

Как найти угол отражения, если известен угол падения и параметры среды, например, показатель преломления?

Если речь идёт именно об отражении (а не преломлении), угол отражения равен углу падения независимо от параметров среды. Однако если учитывается преломление, для вычисления угла преломления используется закон Снеллиуса, а угол отражения всё равно равен углу падения.

Какие практические применения имеет знание угла отражения при расчётах?

Понимание угла отражения помогает в оптике для создания зеркал, настройки оптических приборов и расчёта направлений световых лучей. Также это важно в технологиях лазеров, фотоники и даже в компьютерной графике для реалистичной визуализации отражённых изображений.