Для точного вычисления площади и объема важно понимать формулы и особенности каждой фигуры. Площадь прямоугольника рассчитывается как произведение длины на ширину, а у круга – по формуле π·r², где r – радиус. При вычислении площади треугольника ключевым параметром является высота, опущенная на основание, и формула 0.5·основание·высота.
Объем прямоугольного параллелепипеда равен произведению всех трех измерений – длины, ширины и высоты. Для цилиндра объем определяется как π·r²·h, где h – высота. Важно использовать точные значения радиуса и высоты, чтобы минимизировать ошибку.
Практический совет: всегда проверяйте единицы измерения и приводите их к одной системе перед расчетами. При работе с измерениями в миллиметрах, сантиметрах и метрах, преобразование позволит получить корректные результаты площади и объема, особенно при дальнейшем использовании данных в инженерных или строительных расчетах.
Как рассчитать площадь прямоугольника по длине и ширине
Площадь прямоугольника вычисляется как произведение его длины на ширину. Формула выглядит так: S = a × b, где S – площадь, a – длина, b – ширина.
Длины сторон измеряются в одних и тех же единицах (например, в метрах, сантиметрах или миллиметрах). Результат площади будет в квадратных единицах соответствующей меры (м², см², мм²).
Для точного расчёта используйте измерения с максимальной точностью, учитывая знаки после запятой. Если стороны заданы в разных единицах, предварительно переведите их к одной системе измерения.
Пример: длина прямоугольника равна 5,2 м, ширина – 3,7 м. Площадь вычисляется как 5,2 × 3,7 = 19,24 м².
Проверяйте корректность измерений перед вычислением, чтобы избежать ошибок, влияющих на результат. При необходимости учитывайте дополнительные условия, например, если прямоугольник часть сложной фигуры.
Формулы площади треугольника при известных основаниях и высотах
Площадь треугольника вычисляется по формуле: S = ½ × основание × высота. Основание – любая из сторон треугольника, высота – перпендикуляр, опущенный на это основание из противоположной вершины.
Для треугольника с основанием a и высотой h_a площадь равна S = ½ × a × h_a. Аналогично для основания b и высоты h_b: S = ½ × b × h_b, и для основания c с высотой h_c: S = ½ × c × h_c.
Высоты измеряются строго по перпендикуляру к основанию. Если высота известна косвенно, например, через координаты вершин или через другие параметры, необходимо предварительно найти ее точное значение с помощью тригонометрии или аналитической геометрии.
При вычислении площади по разным основаниям и высотам результат должен совпадать, что служит проверкой правильности расчетов. Различия указывают на ошибку в измерениях или вычислениях высот.
Определение объема куба по длине ребра
Объем куба рассчитывается как куб длины его ребра. Формула объема: V = a³, где a – длина ребра в выбранных единицах измерения.
Для точного результата важно измерять ребро с максимально возможной точностью, учитывая допуски. Если ребро задано в метрах, объем будет в кубических метрах, если в сантиметрах – в кубических сантиметрах.
Пример: если длина ребра равна 5 см, объем равен 5³ = 125 см³.
При вычислении объема с дробными значениями длины ребра рекомендуется использовать калькулятор или программное обеспечение для избежания ошибок округления.
Расчет объема цилиндра на основе радиуса и высоты
Объем цилиндра вычисляется по формуле: V = π × r² × h, где r – радиус основания, h – высота цилиндра, π ≈ 3.1416.
Радиус следует измерять от центра основания до его края. Высота – перпендикулярное расстояние между основаниями. Для точности используйте одинаковые единицы измерения, например, сантиметры.
Подставляя значения в формулу, сначала возведите радиус в квадрат, затем умножьте на π и на высоту. Результат будет в кубических единицах, соответствующих единицам измерения радиуса и высоты.
Для практических расчетов π можно использовать приближенное значение 3.14, а при необходимости высокой точности – 3.14159 или встроенную константу π в калькуляторе.
Если известен диаметр основания, радиус определяется как половина диаметра: r = d / 2. В таком случае формула объема принимает вид: V = π × (d/2)² × h.
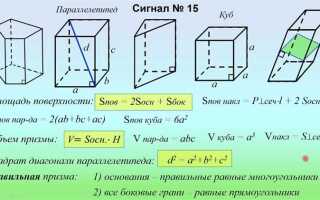
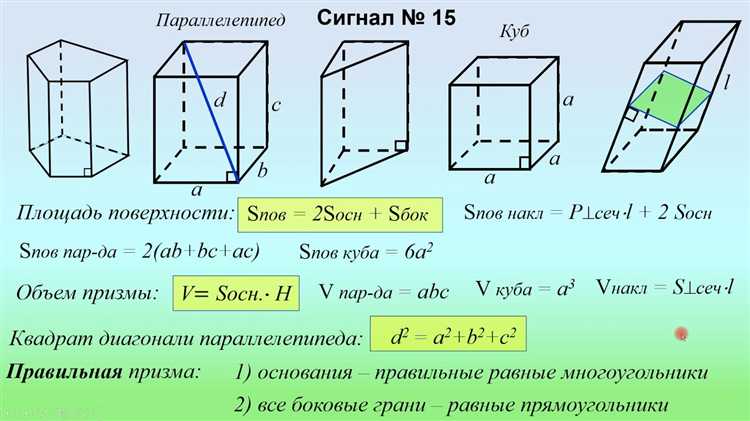
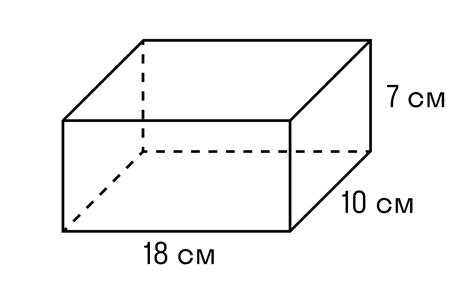
Как найти площадь поверхности и объем прямоугольного параллелепипеда
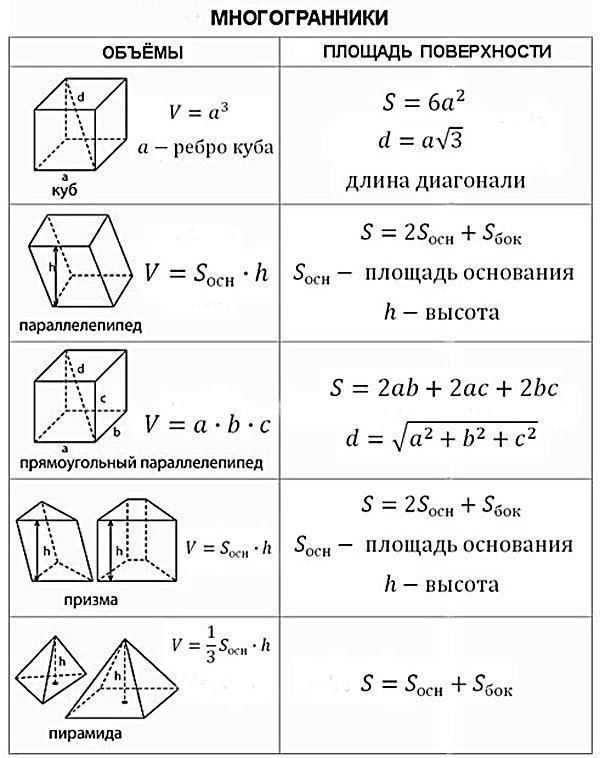
Объем (V) рассчитывается по формуле:
- V = a × b × c
- где a, b, c – длина, ширина и высота соответственно
Площадь поверхности (S) равна сумме площадей всех шести граней. Каждая пара граней имеет одинаковую площадь:
- Площадь одной пары: a × b
- Площадь второй пары: a × c
- Площадь третьей пары: b × c
Формула площади поверхности:
- S = 2(ab + ac + bc)
Для точных вычислений придерживайтесь следующих рекомендаций:
- Измеряйте стороны с одинаковой единицей измерения (например, сантиметры).
- При необходимости перевода площади в квадратные единицы и объема в кубические – учитывайте единичные преобразования.
- Выполняйте умножение в порядке удобства, чтобы избежать ошибок.
- Проверяйте корректность введенных размеров, особенно если фигура создана вручную.
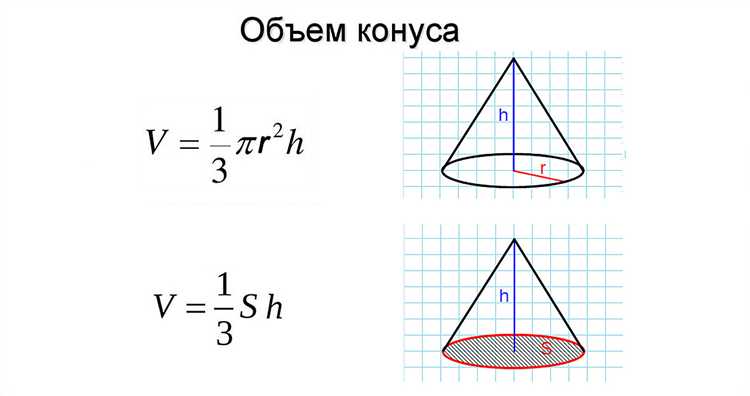
Практические способы вычислить объем конуса с заданной высотой и радиусом
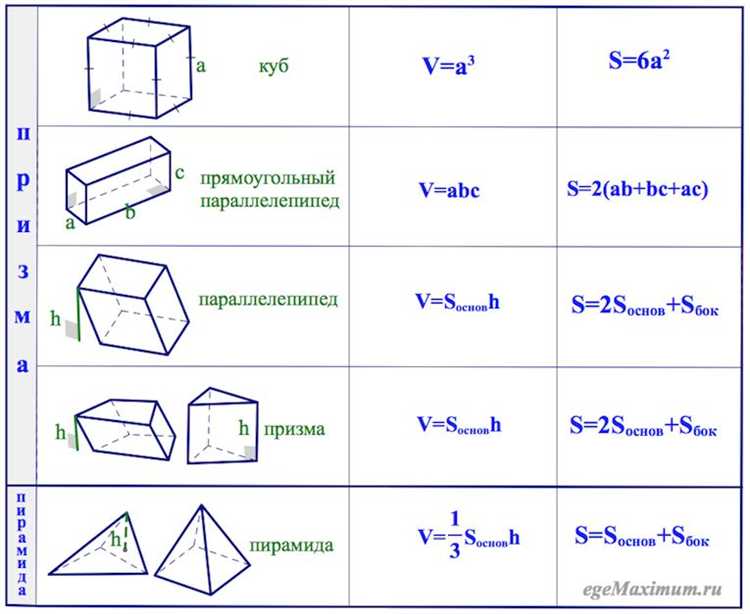
Объем конуса вычисляется по формуле:
V = (1/3) × π × r² × h, где r – радиус основания, h – высота конуса.
Чтобы получить точный результат, следуйте этим рекомендациям:
- Измерение радиуса: используйте штангенциркуль или рулетку, измеряя расстояние от центра основания до его края. Радиус должен быть в тех же единицах, что и высота.
- Определение высоты: высота – перпендикуляр от вершины конуса до основания. Измерьте её строго под прямым углом, избегая наклона.
- Использование числа π: для точных расчетов применяйте значение π ≈ 3.1416. При необходимости округляйте результат до требуемого знака после запятой.
Пошаговый алгоритм вычисления объема:
- Возведите радиус в квадрат: r².
- Умножьте полученное значение на π.
- Результат умножьте на высоту h.
- Разделите произведение на 3.
Пример:
- Радиус основания r = 4 см.
- Высота h = 9 см.
- Вычисление: V = (1/3) × 3.1416 × 4² × 9 = (1/3) × 3.1416 × 16 × 9.
- V = (1/3) × 3.1416 × 144 = 150.7968 см³.
Для проверки правильности расчетов рекомендуется использовать калькулятор с функцией возведения в степень и встроенной константой π. Альтернативно, можно использовать специализированные онлайн-калькуляторы объема конуса, где достаточно ввести радиус и высоту.
Вопрос-ответ:
Как найти площадь прямоугольника, если известны длина и ширина?
Площадь прямоугольника вычисляется умножением длины на ширину. Например, если длина равна 5 см, а ширина — 3 см, то площадь будет 5 × 3 = 15 квадратных сантиметров.
Какая формула используется для расчёта объёма куба, и почему она именно такая?
Объём куба находится по формуле V = a³, где a — длина ребра. Это связано с тем, что куб имеет равные стороны, и объём — это произведение длины, ширины и высоты. Так как все три измерения одинаковы, формула сокращается до возведения ребра в третью степень.
Можно ли вычислить площадь круга без знания радиуса, если известен диаметр?
Да, для этого достаточно разделить диаметр пополам, чтобы получить радиус, а затем применить формулу площади круга S = πr². Например, если диаметр равен 10 см, то радиус будет 5 см, и площадь — примерно 3,14 × 5² = 78,5 квадратных сантиметров.
Как определить объём цилиндра, если известны высота и радиус основания?
Объём цилиндра рассчитывается по формуле V = πr²h, где r — радиус основания, а h — высота. В основе формулы лежит площадь основания (круг) умноженная на высоту. Если радиус равен 4 см, а высота — 10 см, то объём будет около 3,14 × 16 × 10 = 502,4 кубических сантиметра.
Что делать, если фигура состоит из нескольких простых форм — как найти её площадь и объём?
В таком случае фигуру разбивают на отдельные простые части, для каждой считают площадь или объём по соответствующим формулам, а затем складывают полученные значения. Этот метод помогает работать с комплексными объектами, используя базовые вычисления.
Как правильно вычислить площадь прямоугольника?
Площадь прямоугольника находится умножением длины на ширину. Для этого нужно измерить две стороны фигуры — обычно это две смежные стороны, одна из которых считается длиной, другая — шириной. После умножения этих значений получаем площадь в квадратных единицах, например, квадратных сантиметрах или метрах.
Какая формула используется для вычисления объема цилиндра и какие величины необходимо знать?
Для вычисления объема цилиндра применяют формулу V = πr²h, где r — радиус основания цилиндра, а h — его высота. Нужно точно измерить радиус круглого основания и высоту, после чего возвести радиус в квадрат, умножить на высоту и на число π (примерно 3,14). Результат будет выражен в кубических единицах, например, кубических метрах или сантиметрах.