Электромагнитная волна в вакууме распространяется с постоянной скоростью c ≈ 299 792 458 м/с, которая определяется исключительно фундаментальными физическими константами: ε₀ (электрическая постоянная) и μ₀ (магнитная постоянная), где c = 1/√(ε₀μ₀). В отсутствие материи волна не теряет энергию на поглощение или рассеяние, обеспечивая максимально чистую форму передачи энергии и информации.
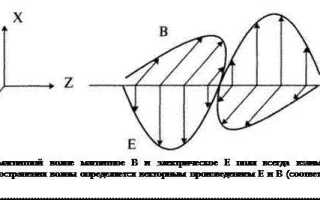
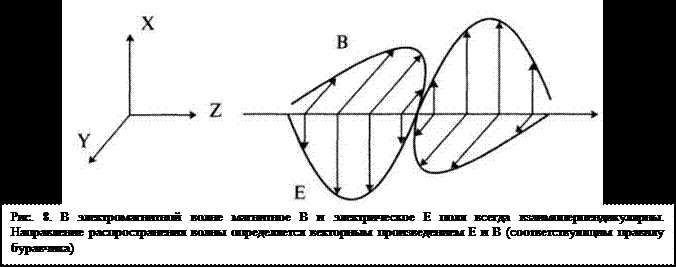
Векторное уравнение Максвелла в вакууме описывает взаимосвязанное поведение электрических и магнитных полей. Электрическое поле E и магнитное поле B осциллируют в плоскостях, перпендикулярных направлению распространения, образуя поперечную волну. При этом E ⊥ B ⊥ k, где k – вектор волнового числа, указывающий направление распространения.
Частота и длина волны сохраняются в вакууме без искажения. Любое изменение характеристик волны связано исключительно с источником или гравитационным влиянием, например, гравитационным красным смещением. Поэтому вакуум используется как эталонная среда при калибровке оптических приборов и при передаче сигналов на межпланетных расстояниях.
Для моделирования и расчёта параметров распространения в вакууме применяются численные методы решения уравнений Максвелла, включая метод конечных разностей во времени (FDTD) и метод моментного анализа. Практическая рекомендация: при расчётах в вакууме не учитывать дисперсию и поглощение, а сосредоточиться на геометрии волны, фазовых соотношениях и граничных условиях в зоне источника и приёмника.
Как скорость света в вакууме определяется через электрическую и магнитную постоянные
Скорость света в вакууме определяется фундаментальными физическими константами – электрической постоянной (ε₀) и магнитной постоянной (μ₀). Эти параметры характеризуют свойства вакуума как среды, в которой распространяются электромагнитные волны.
Электрическая постоянная ε₀ ≈ 8.854187817 × 10⁻¹² Ф/м определяет степень влияния электрического поля на вакуум. Магнитная постоянная μ₀ = 4π × 10⁻⁷ Гн/м определяет аналогичную характеристику для магнитного поля. Взаимосвязь этих констант приводит к точному выражению для скорости света: c = 1 / √(ε₀μ₀).
Подстановка чисел даёт: c = 1 / √(8.854187817 × 10⁻¹² × 4π × 10⁻⁷) ≈ 299 792 458 м/с. Это значение закреплено как точное и определяет метр через временной интервал.
Понимание этой зависимости важно для теоретического анализа уравнений Максвелла, из которых и вытекает данное соотношение. Скорость света не произвольна – она обусловлена внутренними свойствами самого вакуума.
Почему в вакууме электромагнитная волна не теряет энергию при распространении
Физически электромагнитная волна в вакууме – это решение уравнений Максвелла при нулевых токах и зарядах. В таких условиях сохраняется поток энергии, описываемый вектором Пойнтинга. Его дивергенция равна нулю, что указывает на отсутствие утечки энергии в окружающее пространство.
Плотность энергии волны в вакууме определяется выражением: \( u = \frac{1}{2} \varepsilon_0 E^2 + \frac{1}{2\mu_0} B^2 \), где \( \varepsilon_0 \) и \( \mu_0 \) – электрическая и магнитная постоянные, \( E \) и \( B \) – напряжённость электрического и магнитного полей. Величины \( \varepsilon_0 \) и \( \mu_0 \) неизменны, а поля изменяются синхронно и периодически, не создавая условий для необратимого перераспределения энергии.
При отсутствии внешнего воздействия волна сохраняет амплитуду, частоту и фазу на всём протяжении распространения. В отличие от материальных сред, вакуум не вносит дисперсионных и нелинейных эффектов, которые могли бы перераспределять энергию между частотами или модами.
Для расчётов интенсивности используется формула: \( I = \frac{1}{2} c \varepsilon_0 E_0^2 \), где \( c \) – скорость света в вакууме, \( E_0 \) – амплитуда электрического поля. Эта величина остаётся постоянной вдоль направления распространения, что подтверждает отсутствие энергетических потерь.
Как направление вектора Пойнтинга связано с направлением распространения волны
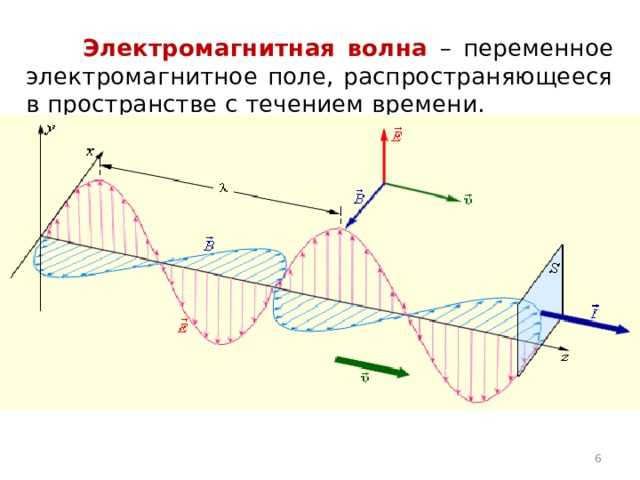
Вектор Пойнтинга S определяется как векторное произведение напряжённости электрического поля E и магнитной индукции B: S = (1/μ₀)(E × B), где μ₀ – магнитная постоянная вакуума. Он указывает направление потока электромагнитной энергии в пространстве.
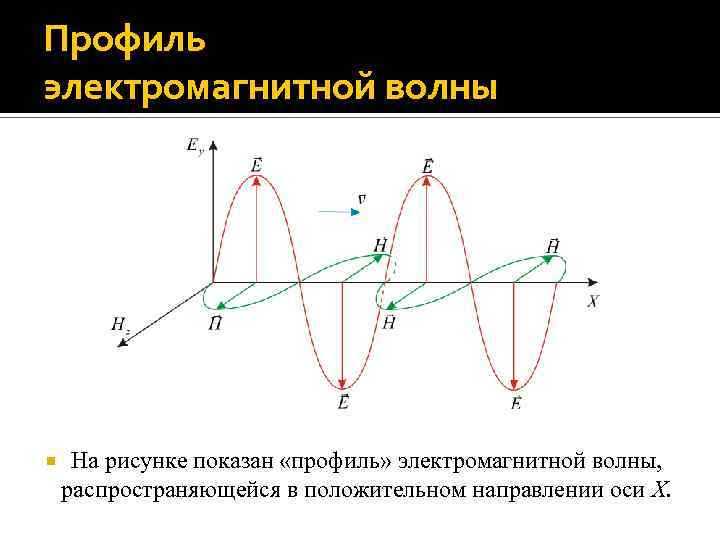
Для плоской монохроматической волны, распространяющейся в вакууме, векторы E и B взаимно перпендикулярны и ортогональны направлению распространения волны. Если волна движется, например, вдоль оси z, а E направлен вдоль x, то B будет направлен вдоль y, и вектор Пойнтинга S окажется направленным вдоль z, совпадая с направлением движения волны.
Таким образом, направление S всегда совпадает с направлением переноса энергии, то есть с направлением распространения волны. Это утверждение справедливо при любом частотном диапазоне в вакууме, поскольку отсутствуют дисперсионные и поглощающие свойства среды.
На практике, для точного определения направления распространения волны, измерение вектора Пойнтинга обеспечивает надёжный критерий: его ориентация прямо указывает на направление энергетического потока, исключая неоднозначности, связанные с направлением полей E и B по отдельности.
Как электрическое и магнитное поля колеблются взаимно перпендикулярно в вакууме
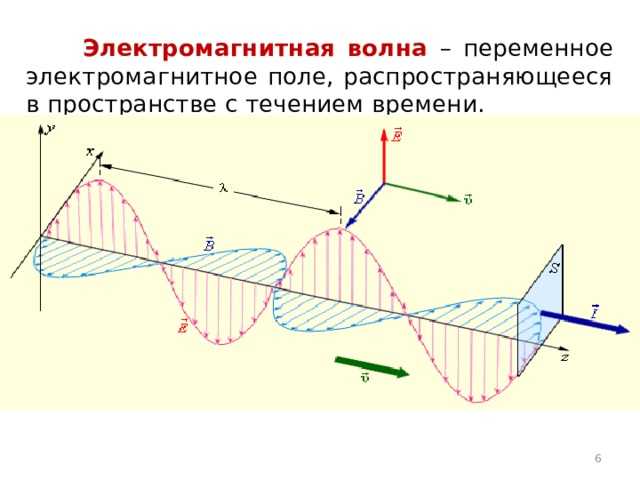
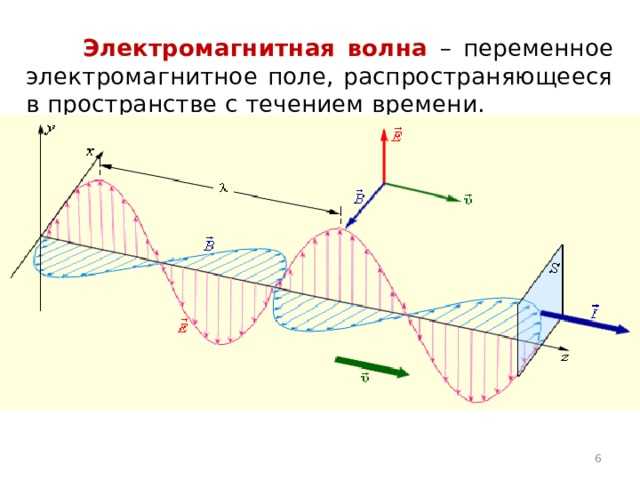
Если волна распространяется вдоль оси z, то электрическое поле колеблется, например, вдоль оси x, а магнитное – вдоль оси y. Эти поля изменяются синусоидально во времени и пространстве с одинаковой фазой. Их амплитуды связаны соотношением B₀ = E₀ / c, где c – скорость света в вакууме, E₀ и B₀ – максимальные значения полей.
Максвелловы уравнения предсказывают, что изменение электрического поля порождает вихревое магнитное поле, и наоборот. В вакууме, где отсутствуют свободные заряды и токи, эти взаимосвязанные колебания поддерживают друг друга и обеспечивают устойчивое распространение волны без затухания.
Колебания строго ортогональны в каждом точечном сечении фронта волны. Это следует из анализа уравнений: ∇ × E = -∂B/∂t и ∇ × B = μ₀ε₀ ∂E/∂t. Условия дивергенции (∇ · E = 0, ∇ · B = 0) исключают продольные компоненты, гарантируя, что поля лежат в плоскости, перпендикулярной направлению волны.
Для точных вычислений применяются решения волнового уравнения вида E(z, t) = E₀ cos(kz — ωt), где k = ω / c – волновое число, ω – угловая частота. Эти функции описывают пространственно-временное поведение полей, полностью согласующееся с теорией Максвелла.
Какие уравнения Максвелла описывают поведение волны в отсутствии среды
В вакууме поведение электромагнитной волны полностью описывается четырьмя уравнениями Максвелла. При отсутствии зарядов и токов (ρ = 0, J = 0) система уравнений принимает следующую форму:
- ∇ · E = 0 – дивергенция электрического поля в вакууме равна нулю. Это указывает на отсутствие свободных зарядов.
- ∇ · B = 0 – магнитное поле не имеет источников, магнитные монополи не существуют.
- ∇ × E = -∂B/∂t – изменение магнитного поля во времени индуцирует вихревое электрическое поле. Это фундаментальный механизм распространения волны.
- ∇ × B = μ₀ε₀ ∂E/∂t – изменение электрического поля порождает вихревое магнитное поле, обеспечивая замкнутый процесс распространения.
Для получения волнового уравнения необходимо применить ротор к уравнениям для E и B:
- Применение оператора ротора к уравнению ∇ × E = -∂B/∂t и подстановка выражения из уравнения ∇ × B = μ₀ε₀ ∂E/∂t дает:
- ∇²E = μ₀ε₀ ∂²E/∂t²
- Аналогично для магнитного поля:
- ∇²B = μ₀ε₀ ∂²B/∂t²
Обе формулы – волновые уравнения. Решения описывают электромагнитную волну, распространяющуюся со скоростью c = 1/√(μ₀ε₀), которая численно совпадает со скоростью света в вакууме:
- c ≈ 3 × 10⁸ м/с
Таким образом, в вакууме электромагнитная волна представляет собой самоподдерживающееся колебание взаимно перпендикулярных электрического и магнитного полей, распространяющееся в пространстве согласно волновым уравнениям, выведенным из уравнений Максвелла.
Как поляризация электромагнитной волны влияет на взаимодействие с приёмными антеннами
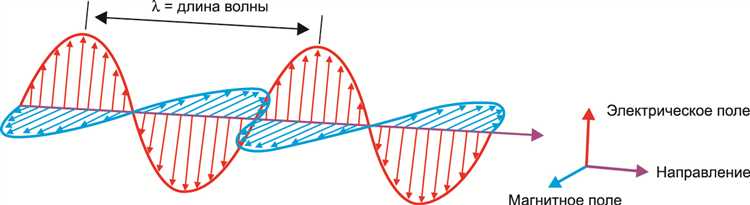
Поляризация электромагнитной волны определяет ориентацию вектора электрического поля относительно приёмной антенны и напрямую влияет на эффективность приёма сигнала. Максимальная мощность принимаемой волны достигается при совпадении поляризации волны и антенны.
Для линейно поляризованных антенн отклонение угла поляризации волны от ориентации антенны приводит к снижению принимаемого сигнала по закону косинуса угла. При разнице в 90° уровень сигнала стремится к нулю. Это особенно критично при использовании направленных антенн в диапазонах УКВ и выше.
Циркулярная поляризация (право- или левовращающая) обеспечивает устойчивость приёма при вращении антенны и изменении направления волны. Однако, приёмо-передающие системы с несовпадающей циркулярной поляризацией (например, правая против левой) испытывают потери порядка 20–30 дБ, что эквивалентно снижению мощности в 1000 раз.
При проектировании систем связи рекомендуется использовать совпадающую поляризацию антенн, либо предусматривать адаптивные приёмные схемы с возможностью переключения поляризации. Для антенн с изменяемой ориентацией (например, мобильных устройств) предпочтительна круговая поляризация для минимизации потерь при движении и наклоне.
Влияние поляризации также заметно при прохождении волн через неоднородные среды или отражениях: изменение поляризации может привести к ухудшению коэффициента стоячей волны и возрастанию интерференционных потерь. Для минимизации подобных эффектов используют поляризационные фильтры и антенны с широкой диаграммой направленности.
Вопрос-ответ:
Почему электромагнитная волна может распространяться в вакууме без носителя?
Электромагнитная волна представляет собой колебания электрического и магнитного полей, которые сами порождают друг друга. Это позволяет волне перемещаться в пространстве без необходимости в среде, так как энергия переносится через взаимодействие этих полей. В вакууме отсутствуют частицы, но поля всё равно могут распространяться благодаря законам электродинамики.
Какая скорость распространения электромагнитных волн в вакууме и от чего она зависит?
В вакууме электромагнитные волны распространяются со скоростью света — примерно 299 792 километров в секунду. Эта скорость не зависит от частоты или длины волны, а определяется фундаментальными физическими свойствами вакуума: электрической и магнитной постоянными. Именно эти константы задают предел скорости передачи электромагнитного излучения.
Какие параметры характеризуют электромагнитную волну в вакууме и как они связаны между собой?
Основные параметры электромагнитной волны включают длину волны, частоту и амплитуду электрического и магнитного полей. Частота показывает, сколько раз в секунду поля совершают полный цикл колебаний, длина волны — это расстояние между двумя соседними максимумами колебаний. Частота и длина волны связаны обратной пропорциональностью через скорость света. Амплитуда определяет интенсивность полей, влияя на энергию волны.
Как изменение среды влияет на распространение электромагнитной волны по сравнению с вакуумом?
В вакууме электромагнитная волна движется с максимальной скоростью и без затухания. При прохождении через различные среды, например воздух или воду, скорость волны снижается из-за взаимодействия с молекулами среды. Также возможны изменения направления, искажение формы волны и снижение интенсивности из-за поглощения и рассеяния энергии. В вакууме таких влияний нет, поэтому волна сохраняет свои характеристики максимально полно.